Системы компьютерной алгебры
Дифференцирование и интегрирование
Для вычисления производной функции f по переменной x используется команда D[f, x]. Нахождениe n -ой производной выглядит так: D[f,{x,n}]. На панели BasicInput имеются кнопки с шаблонами для дифференцирования.
Пример
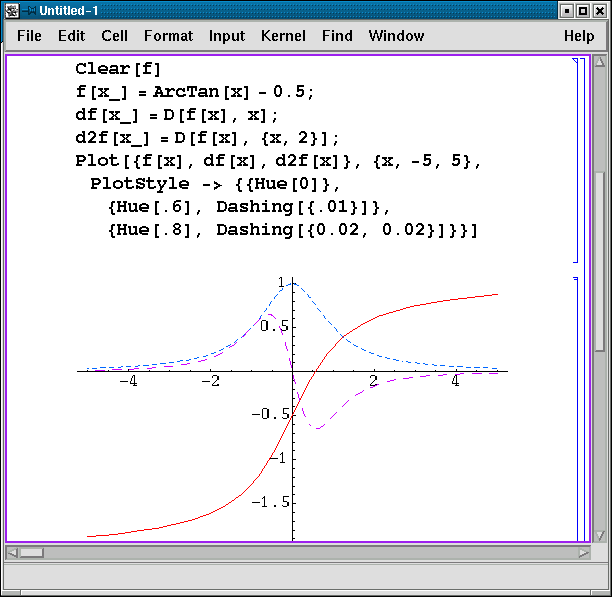
Построим графики функции arctg x - 0.5, ее первой и второй производных. Обратите внимание на определение функций в этом примере. Символ подчеркивания после имени переменной означает, что определяется функция от указанной переменной. Процедура Clear уничтожает данное ранее определение.
Для нахождения первообразной и определенного интеграла применяется функция Integrate, при этом для ввода удобно использовать шаблоны, предоставляемые палитрой Basic Input. Для вычисления кратных интегралов соответствующая функция применяется несколько раз. Ниже представлены примеры использования этой функции.
In[1]:= Integrate[x^2/(4x^6+1), x]
Out[1]:= (1/6) ArcTan[2x^3]
In[2]:= Integrate[1/Sqrt[(4-x)^3],{x,-Infinity,0}]
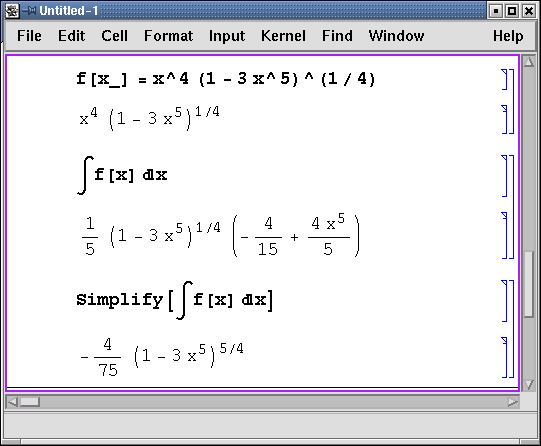
Out[2]= 1Зачастую полезно применить функцию Simplify к результатам вычисления, например,
Задание
- Найдите производные следующих функций:
а) 31-2cos x ; б) (sin x)cos x
- Найдите первообразную функции sin(2x).
- Вычислите определенный интеграл от функции x2 по отрезку [0; 1].
Операции с матрицами
Матрица задается как список списков элементов строк. Для представления списка в традиционной матричной форме используется функция MatrixForm. Процедура Det позволяет вычислять определитель. С помощью функции Dot находится произведение матриц и векторов, но можно использовать и символ . (точка). Inverse находит обратную матрицу, а Transpose используется для транспонирования матрицы (превращения каждой строки в столбец с тем же номером).
Для решения систем линейных уравнений можно использовать функцию LinearSolve или матричный метод, при котором матрица X, содержащая значения неизвестных, находится по формуле X = A-1x B, где x означает операцию умножения матриц.
Пример
Используем указанные способы при решении следующей системы уравнений:
Итак, решением данной системы является тройка {-1, 2.5, 1.5}.
Задания
Логические выражения
Программа Mathematica способна оперировать логическими выражениями. Константы True и False используются для обозначений истинного и ложного утверждений. Кроме констант логические выражения содержат переменные, соединенные следующими связками: And ( &&, конъюнкция), Or ( ||, дизъюнкция), Not ( !, логическое отрицание). Импликация задается функцией Implies или символом из палитры BasicInput. Функция LogicalExpand осуществляет упрощение логических выражений.
из палитры BasicInput. Функция LogicalExpand осуществляет упрощение логических выражений.
Пример
Определим значение логического выражения !(x>z) && !(x=y), если x=3, y=5, z=2
Задание
Получите законы дополнения ( !(!a) = a ), идемпотентности ( a && a = a; a || a = a ) и поглощения ( a && (a || b) = a ) при помощи функции LogicalExpand.




 ,
,
