Управление трафиком
| содержимое ведра до поступления пакетов | содержимое ведра после поступления пакетов | Интервал между поступлениями пакетов | содержимое ведра к моменту следующего поступления | Примечание |
|---|---|---|---|---|
| 0 | 4 | 1 | 3 | |
| 3 | 7 | 3 | 4 | |
| 4 | 8 | 3 | 5 | |
| 5 | 9 | 2 | 7 | |
| 7 | 11 | Пакет не принят | ||
| 9 | 7 | 2 | ||
| 2 | 6 | 7 | 0 | Размерность 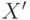 меньше нуля меньше нуля |
| 0 | 4 | 1 | 3 | |
| 3 | 7 | 1 | 6 | |
| 6 | 10 | Пакет не принят | ||
| 10 | 5 | 5 | ||
| 5 | 9 | Далее процесс продолжается |
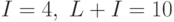
порция поступает через 2 момента времени и содержимое ведра будет равно 7, и если добавить 4 пакета, то это значение 11 превысит глубину ведра. Поэтому ведро не наполняется и продолжает опустошаться. Следующая порция пакетов поступает через 7 интервалов после последнего поступления конформной (принятой) порции пакетов. К этому моменту величина содержимого равна 2, а после добавления она становится равна 6.
Поскольку следующее поступление состоится через 7 интервалов, ведро опустошается до нуля. Далее процесс продолжается аналогичным образом.
Максимальное число обрабатываемых пакетов может быть определено следующим образом.
Если  - количество пакетов, поступающих в один момент времени, а
- количество пакетов, поступающих в один момент времени, а  - время в числе интервалов между двумя поступлениями, то к моменту следующего поступления в буфере окажется
- время в числе интервалов между двумя поступлениями, то к моменту следующего поступления в буфере окажется 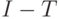 пакетов (предполагаем, что в один интервал времени убывает один пакет). Число шагов, через которое накопится
пакетов (предполагаем, что в один интервал времени убывает один пакет). Число шагов, через которое накопится  пакетов (заполнится пространство
пакетов (заполнится пространство  , равно
, равно
![\left[ \frac {L}{I-T}\right]](/sites/default/files/tex_cache/fc07c4d318b1723d6f587f9d5dde8c8b.png)
где ![[x]](/sites/default/files/tex_cache/3e5314e9fd31509fdeb83faa0f729ba2.png) означает ближайшее целое, меньшее, чем
означает ближайшее целое, меньшее, чем  .
.
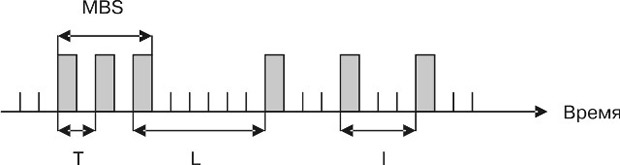
С учетом первого шага разрешенное накопление пакетов не приводящее к потерям MBS (максимальный размер пачки - maximum burst size) определяется выражением ( рис. 7.10).
![MBS = 1+\left[ \frac {L}{I-T}\right]](/sites/default/files/tex_cache/db290349f3eb126c371c8849865de317.png)
увеличить изображение
Рис. 7.10. Параметры передачи трафика, определяемые с помощью принципа "дырявое ведро"
Так, для нашего примера, где 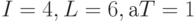
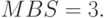
После того как будет накоплено  пакетов, необходим интервал для разгрузки буферной памяти (опустошение ведра) с максимальным значением, равным
пакетов, необходим интервал для разгрузки буферной памяти (опустошение ведра) с максимальным значением, равным  .
.
Величину, обратную 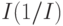 , часто называют поддерживаемой скоростью (Sustainable Rate).
, часто называют поддерживаемой скоростью (Sustainable Rate).
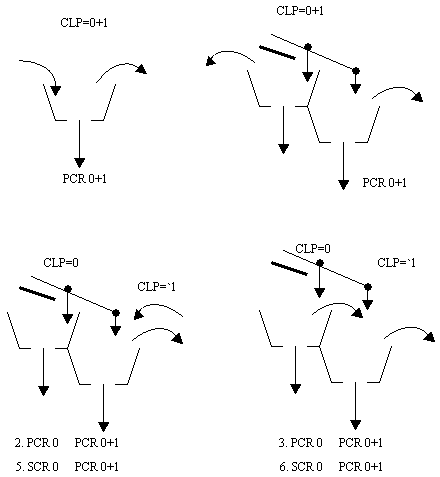
Комбинация дырявых ведер может использоваться для определения нескольких параметров потоков, например пиковой скорости (PCR) и поддерживаемой скорости источника (SCR). В этом случае используются сдвоенные дырявые ведра, показанные на рис. 7.11.
Если в схеме используется два ведра, то в каждое из них направляется равное количество "жидкости", что на рисунке показано диаганальной линией с двумя стрелками. Будем преполагать, что доска, по которой жидкость выливается в дырявые ведра так, что заполняет оба ведра на ту же глубину, как если бы жидкость от одной ячейки была бы плавно вылита в ведро. На рисунке 7.11 показаны следующие конфигурации.
- Основная конфигурация – одиночное ведро, которое позволяет проверить пиковую скорость (PCR 0+1) общего потока ячеек (CLP 0+1).
- Эта конфигурация позволяет проверить соотвествие пиковой скорости ячеек первого приоритета и пиковой скорости общего потока ячеек.
- Конфигурация аналогична конфигурации 2, но меняет значение поля приоритета потери ячейки с 0 на 1
- Эта конфигурация позволяет проверить как пиковую, так и поддерживаемую скорости общего потока ячеек (CLP 0+1). Неконформные ячейки в данной конфигурации отбрасываются.
- и 6. Аналогичны 2 и 3 , но осуществляют проверку как пиковой скорости суммарного потока ячеек (CLP 0 +1), так и поддерживаемую скорость потока ячеек 1-го приоритета (CLP 0).