|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Моделирование сетей, сетевая надежность и сетевые драйверы
Ни один проект крупной сети со сложной топологией в настоящее время не обходится без исчерпывающего моделирования будущей сети. Программы, выполняющие эту задачу, достаточно сложны и дороги. Целью моделирования является определение оптимальной топологии, адекватный выбор сетевого оборудования, определение рабочих характеристик сети и возможных этапов будущего развития. Ведь сеть, слишком точно оптимизированная для решений задач текущего момента, может потребовать серьезных переделок в будущем. Моделирование используется для исследования характеристик новых модификаций протоколов, методы работы с очередями, для оптимизации параметров качества обслуживания.
На модели можно опробовать влияние всплесков загрузки, воздействие большого потока широковещательных запросов или реализовать режим коллапса (для Ethernet), что вряд ли кто-то может себе позволить в работающей сети. В процессе моделирования выясняются следующие параметры:
- предельные пропускные способности различных фрагментов сети и зависимости потерь пакетов от загрузки отдельных станций и внешних каналов;
- время отклика основных серверов в самых разных режимах, в том числе таких, которые в реальной сети крайне нежелательны. Оптимизация конфигурации, например, почтового или WEB-сервера;
- влияние установки новых серверов на перераспределение информационных потоков (Proxy, Firewall и т.д.);
- решение оптимизации топологии при возникновении узких мест в сети (размещение серверов, DNS, внешних шлюзов, организация опорных каналов и пр.);
- выбор того или иного типа сетевого оборудования (например, 10BaseTX, 100BaseFX, GE или 10GE) или режима его работы (например, cut-through, store-and-forward для мостов и переключателей и т.д.);
- выбор внутреннего протокола маршрутизации и его параметров (например, метрики);
- определение предельно допустимого числа пользователей того или иного сервера;
- оценка необходимой полосы пропускания внешнего канала для обеспечения требуемого уровня QOS. Выбор и оптимизация параметров системы обслуживания очередей;
- оценка влияния мультимедийного трафика на работу локальной сети, например, при подготовке видеоконференций;
- выбор протоколов и схемы опорной сети сервис-провайдера и т.д.
Перечисленные задачи предъявляют различные требования к программам. В одних случаях достаточно провести моделирование на физическом (MAC) уровне, в других нужен уже уровень транспортных протоколов (например, UDP и TCP), а для наиболее сложных задач нужно воспроизвести поведение прикладных программ. Все это должно приниматься во внимание при выборе или разработке моделирующей программы. Ведь нужно учесть, что ваша машина должна в той или иной мере воспроизвести действия всех машин в моделируемой сети. Таким образом, машина эта должна быть достаточно быстродействующей, и, несмотря на это, моделирование одной секунды работы сети может занять при определенных условиях не один час.
Задачи моделирования обработки очередей в виртуальном канале с целью оценки параметров качества облуживания требуют не столь значительных ресурсов. Но с учетом перебора возможных значений параметров конфигурации это также может занять много часов.
Результаты моделирования должны иметь точность 10-20%, этого достаточно для большинства целей и не требует слишком много машинного времени. Следует иметь в виду, что для моделирования поведения реальной сети надо знать все ее рабочие параметры: длины кабеля от концентратора до конкретной ЭВМ, задержки используемых кабелей, задержки концентраторов (этот параметр часто отсутствует в документации и его придется брать из документации на сетевой протокол, например, из IEEE 802.3). Параметры могут быть определены и прямым измерением. Чем точнее вы воспроизводите поведение сети, тем больше машинного времени это потребует. Кроме того, вам предстоит сделать некоторые предположения относительно распределения загрузки для конкретных ЭВМ и других сетевых элементов, задержек в переключателях, мостах, времени обработки запросов в серверах. Здесь нужно учитывать и характер решаемых на ЭВМ задач: www/ftp-сервер или обычная персональная рабочая станция создают различные сетевые трафики. Определенное влияние на результат могут оказывать и используемые ОС. В случае моделирования реальной сети можно произвести соответствующие измерения, что иногда тоже не слишком просто. Учитывая сложность моделирования на одной ординарной ЭВМ, следует ограничиваться моделированием не более чем одной минуты для каждого из наборов параметров (этого времени достаточно для копирования практически любого файла через локальную сеть). Исключение может составлять моделирование внешнего трафика, но в этом случае весь локальный трафик должен рассматриваться как фоновый.
Современные распределенные технологии дают новые возможности для решения задач моделирования.
17.1. Аналитическое моделирование
Определение характеристик сети до того, как она будет введена в эксплуатацию, имеет первостепенное значение. Это позволяет отрегулировать характеристики локальной сети на стадии проектирования. Решение этой проблемы возможно путем аналитического или статистического моделирования. По существу, в данном разделе речь идет об описании сети в рамках теории массового обслуживания.
Аналитическая модель сети представляет собой совокупность математических соотношений, связывающих между собой входные и выходные характеристики сети. При выводе таких соотношений приходится пренебрегать какими-то малосущественными деталями или обстоятельствами.
Телекоммуникационная сеть при некотором упрощении может быть представлена в виде совокупности процессоров (узлов), соединенных каналами связи. Сообщение, пришедшее в узел, некоторое время пребывает в очереди до того, как оно будет обработано. Время передачи или полное время задержки сообщения  равно:
равно:
 ,
,
где  ,
,  и
и  соответственно - время распространения, время обслуживания и время ожидания. Одной из задач аналитического моделирование является определение среднего значения
соответственно - время распространения, время обслуживания и время ожидания. Одной из задач аналитического моделирование является определение среднего значения  . При больших загрузках основной вклад дает ожидание обслуживания
. При больших загрузках основной вклад дает ожидание обслуживания  . Для описания очередей в дальнейшем будет использована нотация Д. Дж. Кенделла:
. Для описания очередей в дальнейшем будет использована нотация Д. Дж. Кенделла:
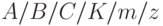 ,
,
где  - процесс прибытия:
- процесс прибытия:  - процесс обслуживания;
- процесс обслуживания;  - число серверов (узлов);
- число серверов (узлов);  - максимальный размер очереди (по умолчанию -
- максимальный размер очереди (по умолчанию -  );
);  - число клиентов (по умолчанию -
- число клиентов (по умолчанию -  );
);  - схема работы буфера (по умолчанию FIFO). Буквы
- схема работы буфера (по умолчанию FIFO). Буквы  и
и  представляют процессы прихода и обслуживания и обычно заменяются следующими буквами, которые характеризуют закон, соответствующий распределения событий:
представляют процессы прихода и обслуживания и обычно заменяются следующими буквами, которые характеризуют закон, соответствующий распределения событий:
-
 - постоянная вероятность;
- постоянная вероятность; -
 - марковское экспоненциальное распределение;
- марковское экспоненциальное распределение; -
 - обобщенный закон распределения;
- обобщенный закон распределения; -
 - распределение Эрланга порядка
- распределение Эрланга порядка  ;
; -
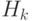 - гиперэкспоненциальное распределение порядка
- гиперэкспоненциальное распределение порядка  .
.
Наиболее распространенными схемами работы буферов являются FIFO (First-In-First-Out), LIFO (Last-In-First-Out) и FIRO (First-In-Random-Out). Например, запись 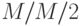 означает очередь, для которой времена прихода и обслуживания соответствует экспоненциальному распределению, имеется два сервера, длина очереди и число клиентов могут быть сколь угодно большими, а буфер работает по схеме FIFO. Среднее значение длины очереди
означает очередь, для которой времена прихода и обслуживания соответствует экспоненциальному распределению, имеется два сервера, длина очереди и число клиентов могут быть сколь угодно большими, а буфер работает по схеме FIFO. Среднее значение длины очереди  при заданной средней входной частоте сообщений
при заданной средней входной частоте сообщений  и среднем времени ожидания
и среднем времени ожидания  определяется на основе теоремы Литла (1961):
определяется на основе теоремы Литла (1961):
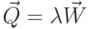
Для варианта очереди 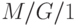 входной процесс характеризуется распределением Пуассона со скоростью поступления сообщений
входной процесс характеризуется распределением Пуассона со скоростью поступления сообщений  . Вероятность поступления
. Вероятность поступления  сообщений на вход за время
сообщений на вход за время  равно:
равно:
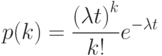
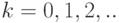 .
.Пусть  - число клиентов в системе,
- число клиентов в системе,  - число клиентов в очереди, и пусть вероятность того, что входящий клиент обнаружит
- число клиентов в очереди, и пусть вероятность того, что входящий клиент обнаружит  других клиентов, равна:
других клиентов, равна:
![П_j=P[n=j], j=0,1,2,... \sum_{j=0}^\infty П_j=1; П_0=1-\rho;\rho=\lambda\tau](/sites/default/files/tex_cache/d9361fb6cca2c32d403aaa9c00d4c910.png)
Тогда среднее время ожидания  :
:
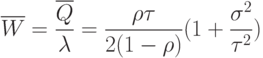
 - среднеквадратичное отклонение для распределения времени обслуживания.
- среднеквадратичное отклонение для распределения времени обслуживания.
Для варианта очереди ![M/G/1 H(t) = P[X \le t] = 1 - e^{-\mu t}](/sites/default/files/tex_cache/1a17efcfcf8673c785cc6ac75768ea8d.png) (
(  - функция распределения времени обслуживания). Откуда следует
- функция распределения времени обслуживания). Откуда следует 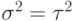 .
.
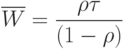
Для варианта очереди 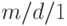 время обслуживания постоянно, а среднее время ожидания составляет:
время обслуживания постоянно, а среднее время ожидания составляет:
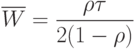
Аналитическая модель для сетей Ethernet (CSMA-CD) разработана Лэмом (S.S.Lam: "A Carrier Sense Multiple Access Protocol for Local Networks," Computer Networks, vol. 4, n. 1, pp. 21-32, January 1980). Здесь предполагается, что сеть состоит из бесконечного числа станций, соединенных каналами с доменным доступом. То есть станция может начать передачу только в начале какого-то временного домена. Распределение сообщений подчиняется закону Пуассона с постоянной скоростью следования  . Среднее значение времени ожидания для таких сетей составляет:
. Среднее значение времени ожидания для таких сетей составляет:
![\overline{D}=\frac{\lambda [S^2+(4e+2)\tau S+5\tau^2+4e(2e-1)\tau^2]}{2(1-\lambda [\overline{S}+\tau+2e\tau])}-\frac{(1-e^{-2\lambda\tau})(e+\lambda\tau-2\lambda\tau e)}{\lambda e[F(\lambda)e^{-(1+\lambda\tau)}+e^{-2\lambda\tau}-1]}+2\tau e+\overline{S}+\tau /3](/sites/default/files/tex_cache/5768b067182f51f1fd6094d35dbffb95.png)
где  - основание натурального логарифма,
- основание натурального логарифма,  - задержка распространения сигнала в сети.
- задержка распространения сигнала в сети. 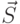 и
и 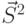 - соответственно первый и второй моменты распределения передачи или обслуживания сообщения.
- соответственно первый и второй моменты распределения передачи или обслуживания сообщения. 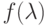 преобразование Лапласа для распределения времени передачи сообщения. Следовательно,
преобразование Лапласа для распределения времени передачи сообщения. Следовательно,
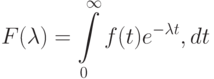
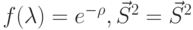 , где
, где 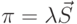 . Для экспоненциального распределения длин сообщений:
. Для экспоненциального распределения длин сообщений: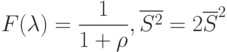
Рассмотрим вариант сети Ethernet на основе концентратора-переключателя с числом каналов  . При этом будет предполагаться, что сообщения на входе всех узлов имеют пуассоновское распределение со средней интенсивностью
. При этом будет предполагаться, что сообщения на входе всех узлов имеют пуассоновское распределение со средней интенсивностью 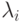 , а распределение сообщений по длине произвольно. Сообщения отправляются в том же порядке, в котором они прибыли. Трафик в сети предполагается симметричным. Очередь имеет модель
, а распределение сообщений по длине произвольно. Сообщения отправляются в том же порядке, в котором они прибыли. Трафик в сети предполагается симметричным. Очередь имеет модель 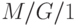 . Среднее время ожидания в этом случае равно:
. Среднее время ожидания в этом случае равно:
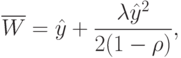
где ![\hat{y}=[1+(N-2)\rho G]\overline{S}](/sites/default/files/tex_cache/1e03218ee9e75ecf9e5561d006d0a70a.png) ,
,
![\hat{y}^2=2[1+(N-2)\rho G+(N-2)(N-3)\rho^2G^2]\overline{S^2}](/sites/default/files/tex_cache/701184295919723d2466547defbf4814.png)
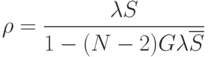
 , а
, а 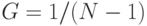 равно вероятности того, что сообщение отправителя
равно вероятности того, что сообщение отправителя  направлено получателю
направлено получателю  . Требование стабильности
. Требование стабильности 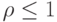 обязывает, чтобы
обязывает, чтобы 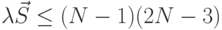
Для больших  это приводит к
это приводит к  .
.
Среднее время распространения сообщения в сети равно 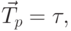 где
где  равно
равно  .
.

Особое место занимает моделирование систем работы с очередями. Эти задачи стали особенно актуальными в связи необходимостью получения гарантированных параметров качества обслуживания. Этот тип моделирования можно реализовать с помощью общедоступной программы NS-2. (Смотри http://www-nrg.ee.lbl.gov/ns/ и http://www-mash.cs.berkeley.edu/ns.)

