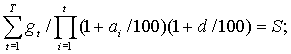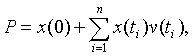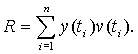Основы принятия решений и ситуационного моделирования

Cитуационный анализ соотношения осложняется рядом факторов:

1. структура активов и пассивов могут отражаться ссудами различной длительности, а также различными схемами размещения и привлечения обязательств и ценных бумаг, например, возврат денег может быть осуществлен по схеме ежемесячного отчисления процентов и уплаты кредита в конце либо по схеме единовременного возврата суммы долга и процентов в конце промежутка кредитования;
2. необходимостью учета (прогноза) инфляционного ожидания и "увеличения" или "очистки" тех или иных составляющих активов и пассивов в зависимости от инфляции;
3. различными параметрами и факторами, влияющими на степень риска, затрудненностью оценки величины риска.

Различные структуры и схемы размещения и привлечения финансовых ресурсов определяют и различные динамические модели.

Например, если схема предусматривает возврат долга с процентами одновременно, реальная ставка рублевого кредита d может быть определена по формуле

d=(z-a)/(1+a/100) (%),

где z - номинальная ставка рублевого кредита (%), а - инфляция за период кредитования (%).

Для валютного кредита, очищенного от инфляции, с учетом внутренней конвертируемости рубля:

d=[((1+z/100)(1+g/100)-(1+a/100))/(1+a/100)]100 (%),

где z - номинальная ставка валютного кредита (%), g - рост курса валюты за период кредитования (%).

Если же договор размещения кредитов предусматривает учет динамики возврата долга (части долга) и уплаты процентов, то реальная ставка может определяться следующей процедурой:

1. определяется динамика срочных выплат (части долга и процентов), гарантирующая полное выполнение обязательств за период кредитования, т.е. обеспечивающая выполнение условий
   

   
   
   где g_t - ежемесячные (ежеквартальные, ежегодные) выплаты, t - номер месяца (квартала, года), в конце которого происходит выплата, S - размер ссуды, выданной в начале договора кредитования, T - количество дней (месяцев, кварталов, лет) кредитования;
2. задается динамика инфляции, например, дискретная функция a_t=a(t), t=1,2,...,T ;
3. определяется реальная ставка d - решение уравнения:
   

   
   
   если кредит - валютный, то необходимо дополнить этапы 1-3 этой процедуры следующими этапами:
4. осуществляется прогноз роста курса валюты, т.е. определяется (задается) дискретная функция g_t=g(t), t=1, 2, :, T ;
5. реальная ставка определяется из уравнения вида ( S - ссуда в валюте):
   

   
   

В долговременных финансово-кредитных операциях проценты либо выплачиваются сразу после их начисления, либо их реинвестируют, применяя сложные проценты. Исходная сумма S (база) увеличивается по принятому (кредитором и дебитором) соглашению, а для простых процентов база постоянная и равна начальной сумме S. Присоединение начисленных процентов к базовой сумме называется капитализацией процентов, t=0,:, T.

Важнейшим показателем при ситуационном анализе и моделировании деятельности и жизнеспособности банка является надежность, банковский или кредитный риск. Надежность банка - не просто вероятность быть надежным банком в данный момент, а вероятность банка сохранять надежностные характеристики и отношения на некотором допустимом промежутке их варьирования и для определенного промежутка времени.

Пусть 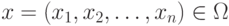- вектор, характеризующий надежность банка, а - некоторое множество его допустимых изменений. В качестве меры надежности можно взять условную вероятность , где P - оценка (степень) надежности, - оценка при условии изменения .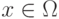

Пример. Пусть - информационные ресурсы, доступные объекту (субъекту), который производит анализ надежности банка, а x=(x₁,x₂,x₃), где x₁ - активы банка, x₂ - пассивы банка, x₃ - дебиторская задолженность банку. Пусть, например, мы хотим оценить надежность банка, но не имеем о банке информации (или имеем нулевую информацию). Тогда значение можно получить, только исходя из двух возможных равновероятных состояний - банк либо надежен, либо не надежен, т.е. 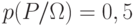. Результат мало информативен и может быть применен к любому банку при любых условиях Пусть теперь известно, что существует лишь 30 % надежных банков, т.е. мы при оценке надежности банка используем эту информацию. В этом случае можно оценить надежность банка как 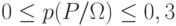. В то же время, как и для предыдущего случая, такая оценка надежности будет малоинформативной, так как здесь мы имеем, как и в первом случае, два возможных состояния ( p<=0,3 и p>0,3 ) и по формуле Шеннона количество информации в том и в другом случае равно

I=log2N=log22=1 (бит).

Чем более точной информацией о банке владеет вкладчик (дебитор), тем проще ему можно принимать верные решения, т.е. тем чаще и ближе будут оценки вероятности (надежности) p к p=0 и p=1. Чем меньше информации, тем сложнее принять однозначное решение, тем чаще и ближе будет оценка вероятности к p=0,5 ("пятьдесят на пятьдесят").

Величину принято называть апостериорной вероятностью (a posteriori - после опыта). Под опытом здесь подразумевается процесс получения информации следовательно, - вероятность быть надежным банком с учетом полученной в результате опыта информации.

При определении надежности (например, экспертами) могут допускаться ошибки, в том числе и субъективного характера. Это - вероятность "ложной классификации". Пусть p₁ - вероятность отнесения (априори) надежного банка в класс ненадежных, а p₂ - вероятность отнесения (априори) ненадежного банка в класс надежных банков. Если не учитывать гипотез о степени их предпочтения (рейтинг банка), то показатель качества классификации - сумма вероятностей совершения ошибок, т.е. p=p₁+p₂. Можно снабдить их весами (предпочтения) a₁ и a₂, например, если a₁=1, a₂=2, то вероятность p₂ в 2 раза важнее p₁ (иначе говоря, в 2 раза опаснее относить ненадежный банк в группу надежных, чем надежный банк в группу ненадежных). Тогда итоговый показатель является средневзвешенной суммой вероятностей:

p=a1q1+a2q2,

где a₁, a₂>=0, q₁, q₂>=0, q₁, q₂ - вероятности ошибок, q₁=1-p₁, q₂=1-p₂.

Показатель p называют байесовским риском. Чем больше p, тем хуже произведена классификация, а чем она ближе к нулю, тем классификация ближе к реальной или априорной классификации.

Для ситуационного анализа необходимо иметь адекватные модели потока платежей. Как правило, этот поток - дискретный. Рассмотрим одну из простых подмоделей модели ситуационного анализа, дополняющую выше приведенную процедуру.

Пусть в момент времени t₀=0 имеется капитал x(0) (денежных единиц), а в момент времени t=t₁, t₂, ...,t_n имеются транзакции (приход, расход) y(t_i), i=1,2,...,n. Рассмотрим, как это бывает на практике, одинаковые промежутки времени (год, месяц, день) [t₀;t₁], (t₂;t₃], ..., (t_n-1; t_n], т.е. t_i-t_i-1=const и векторы t=(0, t₁, t₂,...,t_n), x=(x(0), x(t₁), x(t₂), ..., x(t_n)), y=(0, y(t₁), y(t₂), ..., y(t_n)), v=(0, v(t₁), v(t₂), ..., v(t_n)), где v(t_i) - коэффициент дисконта на промежутке времени (0;t_i], т.е. коэффициент относительной скидки или отношения приращения ссуды (капитала) за срок от 0 до t_i к наращенной сумме. Тогда потоки приходов и расходов будут, соответственно, равны

Будем считать доходы кредитора (инвестора) отрицательными величинами (отдает), а поступления - положительными. Тогда z(0)=-x(0) - начальный доход (начальная величина инвестиций), а z(t_i)=y(t_i)-x(t_i) - поступление на его счет, i=1,2,..., n.

Чистая стоимость потока Q=R-P равна:

Аналогично, чистое наращенное значение потока на момент времени t_i>0 равно (вводя a(t_j, t_i) - коэффициент наращения на ( t_j;t_i],j=1,:,n-1 )

Наращенное значение всех платежей к моменту времени t_n=T равно Q_n.