Эволюционное моделирование и генетические алгоритмы

Пример. Пусть имеется некоторая социально-экономическая среда, которая возобновляет с коэффициентом возобновления 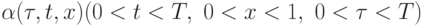свои ресурсы. Этот коэффициент зависит, в общем случае, от мощности среды (ее ресурсоемкости, ресурсообеспеченности). Рассмотрим простую гипотезу: 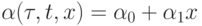, и чем больше ресурсов - тем больше темп их возобновления. Можно записать непрерывную эволюционную модель ( a - коэффициент естественного прироста ресурсов, b - их убыли):

Обозначим . Тогда

Задача всегда имеет решение . Тогда эволюционный потенциал системы можно определить как величину:

Чем выше темп - тем выше 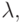чем меньше - тем ниже 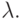Каким бы хорошим ни было состояние ресурсов в начальный момент, они неизменно будут истощаться, если потенциал системы меньше 1.

Пример. Пусть u_max - максимальный уровень синтаксических ошибок в программе Р, u(t) - их оставшееся количество к моменту времени t. Исходя из простейшей эволюционной модели 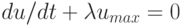, u(t₀)=u₀, можно заключить, что уровень ошибок убывает при 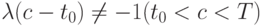по закону: . Если задать дополнительно u(t_*)=u_*, ( u_max - неизвестная величина, ), то закон изменения уровня ошибок находится однозначно, так как: .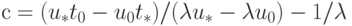

Отметим, что если ds/dt - общее изменение энтропии системы при воздействии на систему, ds₁/dt - изменение энтропии за счет необратимых изменений структуры, потоков внутри системы (рассматриваемой как открытая система), ds₂/dt - изменение энтропии за счет усилий по улучшению обстановки (например, экономической, экологической, социальной), то справедливо уравнение И. Пригожина:

ds/dt = ds1/dt + ds2/dt.

При эволюционном моделировании социально-экономических систем полезно использовать и классические математические модели, и неклассические, в частности, учитывающие пространственную структуру системы (например, клеточные автоматы и фракталы), структуру и иерархию подсистем (например, графы и структуры данных), опыт и интуицию (например, эвристические, экспертные процедуры).

Пример. Пусть дана некоторая экологическая система в которой имеются точки загрязнения (выбросов загрязнителей) x_i, i=1, 2, :, n. Каждый загрязнитель x_i загрязняет последовательно экосистему в промежутке времени (t_i-1; t_i], t_i=t_i-t_i-1. Каждый загрязнитель может оказать воздействие на активность другого загрязнителя (например, уменьшить, нейтрализовать или усилить по известному эффекту суммирования воздействия загрязнителей). Силу (меру) такого влияния можно определить через r_ij, R={r_ij: i=1,2,:, n-1; j=2,3,:, n}.

Структура задаётся графом: вершины - загрязнители, ребра - меры.

Найдём подстановку минимизирующую функционал вида:

где F - суммарное загрязнение системы с данной структурой S.

Чем быстрее (медленнее) будет произведен учёт загрязнения в точке x_i, тем быстрее (медленнее) осуществимы социо-экономические мероприятия по его нейтрализации (усилению воздействия). Чем меньше будет загрязнителей до загрязнителя x_i, тем меньше будет загрязнение среды.

В качестве меры r_ij может быть взята мера, учитывающая как время начала воздействия загрязнителей (предшествующих данной x_j ), так и число, а также интенсивность этих загрязнителей:

где v_ij - весовой коэффициент, определяющий степень влияния загрязнителя x_i на загрязнитель x_j (эффект суммирования), h_j - весовой коэффициент, учитывающий удельную интенсивность действия загрязнителя x_j или интервал 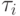, в течение которого уменьшается интенсивность (концентрация) загрязнителя. Весовые коэффициенты устанавливаются экспертно или экспериментально.

Принцип эволюционного моделирования предполагает необходимость и эффективность использования методов и технологии искусственного интеллекта, в частности, экспертных систем.

Основная трудность при построении и использовании эволюционных моделей: в Природе и Познании, в которых эти модели и цели явно или неявно существуют, результаты функционирования системы и достижения цели прослеживаемы часто лишь по прошествии длительного периода времени, хотя в Обществе и Экономике Человек стремится получить результаты в соответствии с целью явно и быстро, с минимальными затратами Ресурсов.