|
Добрый день! Я ранее заканчивал этот курс бесплатно. Мне пришло письмо что я могу по этому курсу получить удостоверение о повышении квалификации. Каким образом это можно сделать не совсем понятны шаги кроме как вновь записаться на этот курс. С уважением Жолондиевский Эрнесто Робертович. |
Функционирование и развитие системы
Основные признаки развивающихся систем:
- самопроизвольное изменение состояния системы;
- противодействие (реакция) влиянию окружающей среды (другим системам), приводящее к изменению первоначального состояния среды;
- постоянный поток ресурсов (постоянная работа по их перетоку "среда-система"), направленный против уравновешивания их потока с окружающей средой.
Если развивающаяся система эволюционирует за счет собственных материальных, энергетических, информационных, человеческих или организационных ресурсов внутри самой системы, то такие системы называются саморазвивающимися (самодостаточно развивающимися). Это форма развития системы - "самая желанная" (для поставленной цели).
Пример. Если на рынке труда повысится спрос на квалифицированный труд, то появится стремление к росту квалификации, образования, что приведет к появлению новых образовательных услуг, качественно новых форм повышения квалификации, например, дистанционных. Развитие фирмы, появление сети филиалов может привести к новым организационным формам, в частности, к компьютеризованному офису, более того, - к высшей стадии развития автоматизированного офиса - виртуальному офису или же виртуальной корпорации. Нехватка времени для шоппинга, например, у занятых и компьютерно грамотных молодых людей с достаточным заработком ("яппи") повлияло на возникновение и развитие интернет-торговли.
Для оценки развития, развиваемости системы часто используют не только качественные, но и количественные оценки, а также оценки смешанного типа.
Пример. В системе ООН для оценки социально-экономического развития стран используют индекс HDI (Human Development Index - индекс человеческого развития, потенциала), который учитывает 4 основных параметра, изменяемых от минимальных до максимальных своих значений:
- ожидаемая продолжительность жизни населения (25-85 лет);
- уровень неграмотности взрослого населения (0-100 %);
- средняя продолжительность обучения населения в школе (0-15 лет);
- годовой доход на душу населения (200-40000 $).
Эти сведения приводятся к общему значению HDI, по которому все страны делятся ООН на высокоразвитые, среднеразвитые и низкоразвитые. Страны с развивающимися ( саморазвивающимися ) экономическими, правовыми, политическими, социальными, образовательными институтами характерны высоким уровнем HDI. В свою очередь, изменение уровня HDI (параметров, от которых он зависит) влияет на саморазвиваемость указанных институтов, в первую очередь - экономических, в частности, саморегулируемость спроса и предложения, отношений производителя и потребителя, товара и стоимости, обучения и стоимости обучения. Уровень HDI, наоборот, также может привести к переходу страны из одной категории (развитости по данному критерию) в другую, в частности, если в 1994 году Россия стояла на 34 месте в мире (из 200 стран), то в 1996 году - уже на 57-м месте; это приводит к изменениям и во взаимоотношениях с окружающей средой (в данном случае - в политике).
Гибкость системы будем понимать как способность к структурной адаптации системы в ответ на воздействия окружающей среды.
Пример. Гибкость экономической системы - способность к структурной адаптации к изменяющимся социально-экономическим условиям, способность к регулированию, к изменениям экономических характеристик и условий.
Траектория системы определяется ее структурой, элементами, окружением. Для простых систем (будем понимать такие системы как системы не свободные в выборе поведения) траекторию можно изменить, лишь изменив элементы, структуру, окружение. Для непростых (сложных - ниже о них подробнее идет речь) систем изменение траектории может произойти и по другим причинам.
Под регулированием (системы, поведения системы, траектории системы) понимается коррекция управляющих параметров по наблюдениям за траекторией поведения системы с целью возвращения системы в нужное состояние, на нужную траекторию поведения. Под траекторией системы понимается последовательность принимаемых при функционировании системы состояний, которые рассматриваются как некоторые точки во множестве состояний системы. Для физических, биологических и других систем - это фазовое пространство.
Для формализации фактов в системном анализе (как и в математике, информатике и других науках) используется понятия " отношение " и "алгебраическая структура ".
Отношение r, определенное над элементами заданного множества Х, - это некоторое правило, по которому каждый элемент  связывается с другим элементом (или другими элементами)
связывается с другим элементом (или другими элементами) 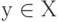 . Отношение r называется n-рным отношением, если оно связывает n различных элементов X. Множество пар (х,у), которые находятся в бинарном (двоичном) отношении друг к другу, - подмножество декартового множества XxY. Отношение r элементов
. Отношение r называется n-рным отношением, если оно связывает n различных элементов X. Множество пар (х,у), которые находятся в бинарном (двоичном) отношении друг к другу, - подмножество декартового множества XxY. Отношение r элементов  ,
,  обозначают как
обозначают как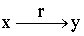 , r(x,y) или r(X,Y).
, r(x,y) или r(X,Y).
Пример. Рассмотрим классическую схему ЭВМ из устройств: 1 - ввода, 2 - логико-арифметическое, 3 - управления, 4 - запоминающее, 5 - вывода. Отношение "информационный обмен" определим так: устройство i находится в отношении r с устройством j, если из устройства i в устройство j поступает информация. Тогда можно это отношение определить матрицей R отношений (наличие r на пересечении строки i и столбца j свидетельствует о том, что устройство i находится в этом отношении с устройством j, а наличие  - об отсутствии между ними этого отношения ):
- об отсутствии между ними этого отношения ):
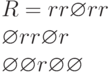
Отношение, задаваемое фразой "для каждого  " обозначается
" обозначается  и называется квантором общности, а отношение "существует
и называется квантором общности, а отношение "существует  " имеет обозначение
" имеет обозначение  и называется квантором существования. Факт того, что элементы
и называется квантором существования. Факт того, что элементы  связаны, выделены некоторым отношением r, обозначают как Х={х: r} или Х={х|r}.
связаны, выделены некоторым отношением r, обозначают как Х={х: r} или Х={х|r}.
Композиция (произведение) r=r1 o r2. отношений r1 и r2, заданных над одним и тем же множеством Х, - это третье отношение r, определяемое правилом:
Отношение r называется отношением 1) тождества; 2) рефлексивным; 3) mpанзитивным; 4) симметричным; 5) обратным к отношению s, если, выполнены, соответственно, условия
Пример. Бинарное отношение равенства чисел "=" - рефлексивное (так как x=x ), симметричное (так как x=y => y=x ), транзитивное (так как x=>y, y=>z => x=>z ). Бинарное отношение "иметь общий делитель" - рефлексивное, симметричное, транзитивное (проверить). Бинарное отношение вложенности множеств "  " - рефлексивное, антисимметричное, транзитивное (проверить).
" - рефлексивное, антисимметричное, транзитивное (проверить).
Частично упорядоченной по отношению r системой Х называется система, для которой (т.е. для любых элементов которой) задано отношение r(Х), являющееся транзитивным, несимметричным, рефлексивным.







