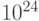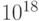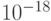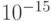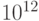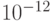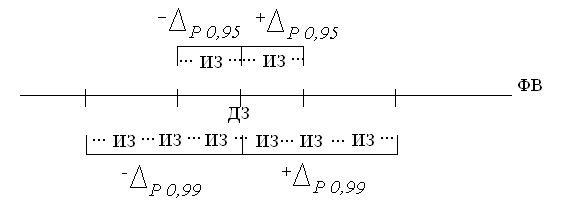|
Пришлите пожалуйста на почту мне pdf - версию сертификата. |
Основные сведения из метрологии
1.7. Система СИ
Международная система единиц, сокращенно СИ ( SI - начальные буквы французского наименования System International ).
В России система СИ принята на уровне стандарта в 1981 году. В 2002 году принята новая версия стандарта: ГОСТ 8.417-2002 "ГСИ. Единицы физических величин" [2]. Стандарт устанавливает единицы физических величин, наименования, обозначения, определения и правила применения этих единиц. Стандарт не устанавливает единицы величин, оцениваемых по условным шкалам, единицы количества продукции, а также обозначения единиц физических величин для печатающих устройств с ограниченным набором знаков (ГОСТ 8.430).
В качестве основных, согласно классификации СИ, приняты семь единиц: метр, килограмм, секунда, ампер, кельвин, моль, канделла. Им соответствуют следующие физические величины: длина, масса, время, сила электрического тока, термодинамическая температура, количество вещества, сила света.
Производная единица в системе СИ образуется из одной или нескольких основных единиц. Многим производным единицам присвоены собственные наименования (скорость, площадь). Семнадцати производным единицам присвоены собственные наименования по именам ученых.
Основные физические величины отображают наиболее естественные для современного человека свойства окружающего мира. Размеры единиц физических величин выбраны такими, чтобы они комфортно воспринимались органами чувств человека. Основные величины, согласно классификации СИ, приведены в табл. 1.1.
| Физическая Величина | Единица физической величины | ||||
|---|---|---|---|---|---|
| Наименование | Обозначение | Наименование | Обозначение | ||
| Размерность | Физическая величина | Рос. | Международное | ||
| Длина | L |  |
метр | м | m |
| Масса | М |  |
килограмм | кг | kg |
| Время | T |  |
секунда | с | s |
| Сила эл. тока | I |  |
ампер | А | А |
| Т/д-я температура |  |
 |
кельвин | К | К |
| Количество вещества | N |  |
моль | моль | mol |
| Сила света | J |  |
канделла | кд | cd |
Для образования кратных и дольных единиц предусмотрены множители и приставки. Таблица 1.2 содержит множители и приставки согласно классификации СИ.
ГОСТ8.417-2002 наряду с единицами физических величин определяет единицы количества информации:
- бит, байт, ( bit, byte ),
- килобит, килобайт, Кбит, КБ ( kbit, kB ).
Стандартом МЭК 60027-2 от 01.1999 [3] определены более полные характеристики единиц количества информации (двоичных, или бинарных единиц), с определением бинарных приставок и множителей. Бинарные приставки: килобинарибит, килобинарибайт ( Kibit, KiB ).
При работе с двоичными единицами удобнее принимать за один килобайт не 1000 байт, а 1024 байт. Однако при этом возникает разночтение приставок, принятых в СИ. Это препятствует единству измерений. Для исключения разночтения, приняты собственные приставки для двоичных единиц, созвучные приставкам, принятым в системе СИ, но дополненные приставкой "бинари".
Эти сведения не нашли отражения в системе СИ, определенной ГОСТ8.417-2002. Стандарт, аналогичный МЭК 60027-2 от 01.1999, пока не принят в российской системе стандартизации. Поэтому сведения о двоичных множителях и приставках приведены только в международном варианте (табл. 1.3). В таблице 1.4 сопоставляются множители и приставки двоичные и принятые по классификации СИ.
| Prefixes for binary multiples | ||||
|---|---|---|---|---|
| Factor | Name | Symbol | Origin | Derivation |
 |
kibi | Ki |  |
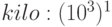 |
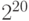 |
mebi | Mi | 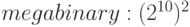 |
 |
 |
gibi | Gi |  |
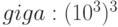 |
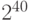 |
tebi | Ti | 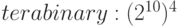 |
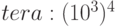 |
 |
pebi | Pi | 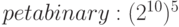 |
 |
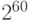 |
exbi | Ei | 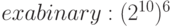 |
 |
| Examples and comparisons with SI prefixes | |
|---|---|
| one kibibit | 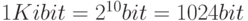 |
| one kilobit |  |
| one mebibyte |  |
| one megabyte | 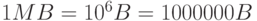 |
| one gibibyte |  |
1.8. Истинное и действительное значение физической величины, погрешность и вероятность
Физическая величина (кратко "величина") - свойство, в качественном отношении общее многим объектам, а в количественном отношении индивидуальное для каждого объекта.
Количественное содержание этого свойства в объекте является размером физической величины. Получение информации о размере величины является содержанием любого измерения. Величину, которой присвоено числовое значение, равное единице, называют единицей физической величины.
Истинное значение физической величины идеальным образом отражает соответствующее свойство объекта. Практически получено быть не может.
Действительное значение физической величины находится как результат измерения и приближается к истинному значению настолько, что для данной цели может применяться вместо него.
Изображенная на
рис.
1.1 диаграмма отображает взаимосвязь понятий истинное значение (ИЗ), действительное значение (ДЗ) физической величины (ФВ), погрешность (  ), вероятность
), вероятность 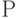 .
.
Очевидно, что истинное значение с заданной вероятностью оказывается удалено от найденного в процессе измерения действительного значения на интервал, не превышающий погрешности. При прочих равных условиях (в первую очередь - при одинаковом числе наблюдений), если требуется назначить большую вероятность, интервал погрешности также возрастает.
Размеры  и
и  взаимосвязаны: чем больше
взаимосвязаны: чем больше  , тем больше
, тем больше  , следовательно, назначая высокую степень уверенности, мы рассматриваем наихудший вариант контролируемых событий. И наоборот, делая более неопределенными контролируемые посредством измерений события, мы получаем большую уверенность в том, что они произойдут. Например, вероятность того, что ракета попадет в точку, оставленную карандашом, близка к нулю. Если постепенно увеличивать размеры точки до размеров земного шара, то вероятность попадания ракеты в эту точку будет постепенно приближаться к единице.
, следовательно, назначая высокую степень уверенности, мы рассматриваем наихудший вариант контролируемых событий. И наоборот, делая более неопределенными контролируемые посредством измерений события, мы получаем большую уверенность в том, что они произойдут. Например, вероятность того, что ракета попадет в точку, оставленную карандашом, близка к нулю. Если постепенно увеличивать размеры точки до размеров земного шара, то вероятность попадания ракеты в эту точку будет постепенно приближаться к единице.
Практически важным является требование одновременно увеличивать  и уменьшать
и уменьшать  . Такую возможность дает увеличение числа наблюдений. Увеличением числа наблюдений можно добиться, соответственно, роста
. Такую возможность дает увеличение числа наблюдений. Увеличением числа наблюдений можно добиться, соответственно, роста  при фиксированной
при фиксированной  , или же уменьшения
, или же уменьшения  при фиксированной
при фиксированной  .
.
Из этих рассуждений становится понятно, почему не следует стремиться к максимальной точности измерений или требовать чрезмерно высокую достоверность результатов. Это потребует дополнительных наблюдений, сделает измерения слишком дорогими.