Рекурсивные программы
Упрощение итеративной версии
Код, данный выше, в сравнении с исходным рекурсивным вариантом выглядит громоздким. Действительно, для серьезного рекурсивного алгоритма итеративная версия никогда не будет выглядеть столь же элегантной, как рекурсивная. Но мы попытаемся приблизиться к этому эталону, пересмотрев источники компиляции.
- Мы можем заменить goto конструкциями структурного программирования.
- Идентифицируя обратимые преобразования аргументов, можно ограничить объем хранимой информации в записи активации, которую нужно записывать и получать из стека.
- В некоторых случаях (хвостовая рекурсия) можно вообще обойтись без стека.
Последние два случая упрощений могут быть также важны для улучшения производительности, поскольку операции над стеком требуют и времени, и памяти.
В примере с Ханойской башней первым делом устраним торчащие как заноза операторы goto. Чтобы абстрагироваться от лишних деталей кода, запишем тело процедуры iterative_hanoi в виде:
INIT
start: if count > 0 then
SAVE_AND_ADAPT_1
goto start
after_1: MOVE
SAVE_AND_ADAPT_2
goto start
end
after_2: if not stack.is_empty then
RETRIEVE
if call = 2 then goto after_2 else goto after_1 end
end
Здесь SAVE_AND_ADAPT_1 представляет сохранение информации в стеке и изменение значений перед первым вызовом, SAVE_AND_ADAPT_2 – то же для второго вызова, RETRIEVE – получение информации из стека, включая значение call, MOVE – базисную операцию переноса, INIT – инициализацию локальных переменных значениями аргументов.
Ранее, при обсуждении вопроса избавления от goto подобный пример уже был рассмотрен. Еще раз проанализировав его, нетрудно понять, что наша программа может быть записана с циклами, но без goto:
from INIT until over loop
from until count <= 0 loop
SAVE_AND_ADAPT_1
end
from stop := stack.is_empty until stop loop
RETRIEVE
stop := (stack.is_empty or (call /= 2))
end
over := (stack.is_empty and (call = 2))
if not over then MOVE ; SAVE_AND_ADAPT_2 end
end
И этот вариант можно упростить, удалив, в частности, булевскую переменную stop:
from INIT until over loop
from until count = 0 loop SAVE_AND_ADAPT_1 end
from call := 2 until stack.is_empty or call = 1 loop RETRIEVE end
over := (stack.is_empty and (call = 0))
if not over then MOVE ; SAVE_AND_ADAPT_2 end
end
Упрощения являются результатом анализа возможных значений переменных.
- Так как count никогда не может стать отрицательной величиной из-за предусловия, требующего его положительности, и условия завершения вычислений, то вполне законно заменить тест count <= 0 на тест count = 0.
- Для избавления от stop заметим, что значение call может быть только 1 или 2, так что допустимо заменить тест call /= 2 на тест call = 1. После чего установим начальное значение call = 2, так что это условие будет учитываться для второй и последующих итераций, если таковые будут.
Хвостовая рекурсия
Стандартная техника, позволяющая уменьшить затраты на операции над стеком по вталкиванию и выталкиванию элементов, основана на том, что нет необходимости хранить контекстную информацию, а позже получать ее, если алгоритму эта информация больше не нужна. В частности, это происходит при рекурсивном вызове, который является последней операцией, выполняемой экземпляром рекурсивной программы.
Это упрощение применимо к примеру hanoi. Второй рекурсивный вызов является последним оператором, выполняемым при активации процедуры. Это означает, что нет необходимости в SAVE_AND_ADAPT_2, или, более точно, единственная информация, которую требуется сохранить, – это значение call, так как при возврате необходимо анализировать это значение.
Хороший компилятор может обнаружить хвостовую рекурсию и применить эту оптимизацию для улучшения производительности рекурсивного алгоритма.
В случае с hanoi устранение хвостовой рекурсии может и не проводиться, так как существует другая, более мощная оптимизация, почти полностью устраняющая необходимость в стеке, с которой мы вскоре познакомимся. Но все же следует освоить на практике оптимизацию, связанную с хвостовой рекурсией, удалив операции, в которых нет необходимости.
Преимущества обратимых функций
Использование стека для хранения значений перед вызовом и получение их после завершения вызова – это техника по умолчанию, которая работает во всех случаях; но мы уже видели ранее, что существует альтернатива данному подходу – обращение преобразования аргументов. В случае с hanoi обращение возможно для всех аргументов.
- Трансформация, применяемая при каждом вызове, count:= count - 1, имеет очевидное обращение: count:= count + 1.
- Для других аргументов, представляющих стержни, трансформация задается операцией взаимного обмена: swap23 – для первого вызова и swap12 – для второго, где swapij означает операцию обмена между стержнями с номерами i и j. Понятно, что эта трансформация обратима, более того, swapij является собственным обращением, поскольку двойной обмен восстанавливает исходное состояние.
Так что, фактически, нет необходимости хранить в стеке ни count, ни x, y, z. Достаточно при достижении RETRIEVE выполнять соответствующее обращение:

Стек остается необходимым, но только для записи и получения call. Упрощение становится еще существеннее, если вспомнить, что call имеет только два значения: 1 и 2. Но ничто не мешает нам изменить соглашение и рассматривать их как булевские значения 1 и 0. Тогда можно применить стек, содержащий булевское значение. Более того, если допустимо ограничить высоту стека, то вместо стека можно использовать единственную целочисленную переменную, скажем, s (в современных компьютерах целочисленные переменные могут иметь длину в 64 бита). Тогда операции над стеком моделируются операциями над целым s, рассматриваемым как строка битов:
s = 1 — Пуст ли стек?
s := 1 — Инициализация пустого стека
s := 2*s — Втолкнуть 0 (сдвиг влево на один разряд строки битов)
s := 2*s + 1 — Втолкнуть 1 (сдвиг влево на один разряд строки битов с
— приписыванием 1)
b := s \\ 2 — Получить (в b) значение с вершины стека
— (\\ остаток от деления нацело)
s:= s // 2 — Удалить значение с вершины стека
— (// - деление нацело – сдвиг вправо)
Вот результат выполнения некоторой последовательности таких операций.
| Оператор | Цель | Результат | Бинарное представление s (часть нулей слева опущена) |
|---|---|---|---|
| s:= 1 | — Начать с пустого стека | s = 1 | 1 |
| s:= 2*s | — Втолкнуть 0 | s = 2 | 10 |
| s:= 2*s + 1 | — Втолкнуть 1 | s = 5 | 101 |
| s:= 2*s + 1 | — Втолкнуть 1 | s = 11 | 1011 |
| s:= 2*s | — Втолкнуть 0 | s = 22 | 10110 |
| s:= s // 2 | — Вытолкнуть | s = 11 | 1011 |
| b:= s \\ 2 | — Прочитать элемент вершины | b = 1 |
В последнем столбце показано бинарное представление целого. Если нумеровать разряды в этом представлении справа налево, начиная с 0, то единица в разряде  имеет значение
имеет значение 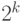 . Значение 0 в самом правом разряде означает, что число четное, 1 – нечетное. Когда такое представление задает стек булевских значений, вершиной стека является самый правый разряд. Пустой стек задается значением
. Значение 0 в самом правом разряде означает, что число четное, 1 – нечетное. Когда такое представление задает стек булевских значений, вершиной стека является самый правый разряд. Пустой стек задается значением  , равным 1.
, равным 1.
Техника использования единственного целого числа для задания стека булевских значений может безопасно использоваться, когда гарантируется, что размер стека не превосходит длины целого в битах. В примере с Hanoi проблемы не возникает, поскольку  или даже
или даже  – число, задающее количество ходов, столь велико, что компьютеру не справиться с вычислениями за разумное время.
– число, задающее количество ходов, столь велико, что компьютеру не справиться с вычислениями за разумное время.
В результате обсуждений приходим к более простой и эффективной форме алгоритма iterative_hanoi с аргументами n, source, target, other:
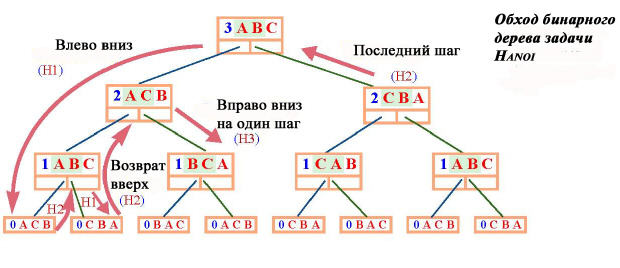
Хотя полученная программа является результатом систематических трансформаций, а не программой, которую вы бы написали с самого начала (рекурсия яснее и проще), интересно проследить за ее выполнением, сравнивая с оригинальной рекурсивной версией, а особенно – с бинарным деревом выполнения, представленным в начале этой лекции и показывающим выполнение как инфиксный обход дерева:
В алгоритме можно выделить три компонента.
| H1 | Самый левый в глубину – идти насколько возможно вниз, влево, пока не достигнешь листа. У листьев значение n = 0 (count в этой версии), хотя на предыдущих рисунках дерево заканчивалось на 1, поскольку на нулевом уровне ничего не происходит. |
| H2 | Возврат вверх. Если вы возвращаетесь из правого поддерева, то продолжаете идти вверх, поскольку это означает завершение второго рекурсивного вызова, а следовательно – и завершение работы текущего экземпляра процедуры. |
| H3 | Поднявшись вверх по левой ветви, выполняем посещение корня – перенос диска из x на y, а потом идем вниз по правой ветви. |
Все это повторяется, пока, придя справа (H2), не обнаружим, что стек пуст.
При спуске вниз (H1, H3) уменьшается count и выполняется обмен y и z, если идем слева (H1), и обмен x и z, если идем справа (H3). При возврате назад (H2) восстанавливаются исходные значения, увеличивая count и выполняя подходящий обмен в зависимости от того, справа или слева вы пришли. Анализ вершины стека, хранящей значение call, позволяет понять, откуда мы пришли в узел – слева (первый вызов) или справа (второй вызов).
9.5. Ключевые концепции, рассмотренные в этой лекции
- Часто удобно определять понятие рекурсивно. Это означает, что определение понятия использует один или несколько экземпляров самого понятия.
- Чтобы такое определение было полезным, любое вхождение понятия должно применяться к меньшей цели в сравнении с исходной. Необходимо также существование нерекурсивной ветви, что позволяет, в конечном счете, любое применение определения свести к конечной комбинации элементарных вариантов.
- Рекурсивные определения, в частности, могут быть полезными при определении программ, структур данных и грамматик.
- Любой цикл может быть записан в эквивалентной рекурсивной форме, используя простую трансформацию.
- Справедливо и обратное. Любой рекурсивный алгоритм имеет свободный от рекурсии эквивалент, но трансформация нужна более изощренная. Она требует изменения потока управления, сохранения локальной информации о каждом рекурсивном вызове, так же как и получение ее в процессе дальнейшей работы. Эта трансформация предполагает работу со стеком или использование обратимых трансформаций данных.
Новый словарь
9.6. Упражнения
9.6.1. Словарь
Дайте точные определения терминам словаря.
9.6.2. Не слишком ли много рекурсии?
Является ли определение "рекурсивного определения" рекурсивным?
9.6.3 Бинарные деревья поиска с повторениями
Для каждого приведенного в этой лекции метода поиска в бинарных деревьях перепишите объявление (если требуется), допуская возможность множественного вхождения элемента item в дерево.
9.6.4. Язык программирования без программных текстов
Напишите компилятор и интерпретатор элементарного языка программирования. Используйте приемы, обсуждаемые в предыдущих лекциях. Решение должно использовать рекурсию. Чтобы избежать проблем с конкретным синтаксисом, ваш инструментарий должен иметь дело непосредственно со структурами данных, а не с текстом программы.
Наш маленький язык, назовем его АСТ ("Абстрактный синтаксис только"), имеет следующие свойства.
- Единственный тип данных – integer.
- Все переменные принадлежат типу integer. Они не объявляются. Имя переменой – любая строка символов.
- Разрешается использовать целочисленные константы, например, 123.
- Выражения формируются из констант, переменных скобок и четырех операций – сложение, вычитание, умножение и деление нацело.
- В языке два вида операторов – присваивание и печать.
- Программа на АСТ состоит из последовательности присваиваний и последовательности операторов печати, каждая из которых может отсутствовать.
- Выполнение программы состоит из инициализации нулями переменных программы,выполнении последовательности присваиваний и последующей печати значений переменных.
Типичная программа на АСТ приведена здесь с учетом конкретного синтаксиса, хотя он и не является частью определения языка:
assign
x := 3
y := 5
x := 2*(x + (y // 3))
then
print x
print z
end
В результате выполнения этой программы должно быть напечатано одно значение – 8.
Синтаксис конкретной программы является одним из возможных выборов. Вполне возможно, например, вместо слова then использовать ключевое слово print. Печать переменных можно задавать списком без повторения print.
Напишите множество классов, включающее PROGRAM, ASSIGNMENT, PRINT, EXPRESSION. Методы этих классов, включающие процедуры создания, должны позволять построить абстрактное синтаксическое дерево, задающее АСТ-программу.
- Добавьте класс с процедурой, которая использует эти классы и их методы для создания абстрактного синтаксического дерева, представляющего программу нашего примера.
- Добавьте в класс PROGRAM процедуру write_out, которая выполняет текстуальное представление АСТ-программ в том виде, как оно дано в примере. Выполните программу из шага 2 и убедитесь в корректности полученного результата. Подсказка: вам необходима рекурсивная процедура обхода, подобная той, которая рассматривалась в данной лекции.
- Напишите АСТ-интерпретатор в форме процедуры interpret в классе PROGRAM, который выполняет программу и вырабатывает ожидаемый результат. Запустите ее на данном примере и проверьте результат выполнения.
- Напишите АСТ-Eiffel-компилятор в форме процедуры compile в классе PROGRAM, которая АСТ-программу преобразует в программу на Eiffel, сохраняя семантику АСТ-программ. Корневой класс с подходящей процедурой создания и другие классы необходимы для решения этой задачи. Используя Eiffel-студию, выполните наш пример и проверьте результат.
Терминологическое замечание. Результатом шага 5 является реанализатор – unparser, который создает текст программы по внутреннему представлению, такому как абстрактное синтаксическое дерево, выполняя операцию, обратную тому, что делает классический анализатор – parser.
9.6.5. Вставка без рекурсии
Напишите версию put для бинарного дерева поиска, используя цикл, а не рекурсию.
Подсказка: источником вдохновения может служить реализация метода has.
9.6.6. Рекурсивный реверс
Сохраняя предположения (список остановок известен своей первой ячейкой типа STOP, остальные остановки доступны через повторное применение next), перепишите функцию reversed, используя рекурсию вместо цикла (смотри также следующее упражнение).
9.6.7. Реверс списка. Функциональный стиль
Напишите рекурсивную функцию для обращения связного списка (аргумент и результат должны быть типа LINKED_LIST[G]). Сведите к минимуму манипуляции с указателями и приблизьтесь, насколько возможно, к стилю функции reversed, приведенному как пример программирования на Haskell. Проанализируйте временную и емкостную сложность вашего решения.
9.6.8. Сокращение перебора с возвратами
Адаптируйте общий алгоритм перебора с возвратами так, чтобы он сохранял историю ранее исследованных позиций и удалял любой путь, ведущий к такой позиции. Можете предположить, что PATH имеет запрос position, определяющий терминальную позицию пути.
9.6.9. Игнорирование циклов
Адаптируйте общий алгоритм перебора с возвратами так, чтобы он не исследовал пути длиннее, чем path_cutoff – заданное целое число.
9.6.10. Свойства графа функции
(Это упражнение не требует программирования, но предполагает проведение математического анализа)
Для последовательных аппроксимаций 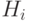 графа функции, связанной с Ханойской башней (параграф 5.7: "Башни снизу вверх"), определите:
графа функции, связанной с Ханойской башней (параграф 5.7: "Башни снизу вверх"), определите:
- Каково число пар в
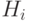 ?
? - Задайте математическую формулу для
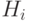 .
.
9.6.11. Программирование графа функции снизу вверх
- Спроектируйте класс, каждый экземпляр которого задает пару "аргумент-результат" в форме [(n, s, t, o),<…>] для графа функции, связанной с Ханойской башней.
- Основываясь на классе из пункта 1, спроектируйте класс, представляющий граф функции в целом.
- Из этих классов и правил (5.5) и (5.6) (параграф 5.7: "Башни снизу вверх"), определяющих граф функции в интерпретации рекурсии "снизу вверх", напишите программу, которая для любого i вычисляет i-ю аппроксимацию графа
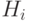 . Алгоритм может использовать циклы, но не может использовать рекурсию.
. Алгоритм может использовать циклы, но не может использовать рекурсию. - Используйте эту программу для печати последовательности ходов (с источником 'A' и целью 'B') для нескольких значений i. Убедитесь, что результаты соответствуют работе рекурсивной процедуры.
9.6.12. Алгоритмы бинарного дерева с точки зрения "снизу вверх"
Рассмотрим рекурсивный алгоритм обхода бинарного дерева: вы можете выбрать префиксный, инфиксный или постфиксный порядок обхода.
- Спроектируйте модель, которая интерпретирует обход как функцию, возвращающую последовательность узлов. Источником вдохновения может служить анализ "снизу вверх" для Ханойской башни.
- Напишите рекурсивное "определение" этой функции.
- Выразите это "определение" в виде уравнения неподвижной точки на графе функции, используя
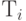 , как имя графа для бинарного дерева высоты i.
, как имя графа для бинарного дерева высоты i. - Используйте это определение для создания (либо вручную, либо написав небольшую программу)
 для примера бинарного дерева и результирующего порядка обхода.
для примера бинарного дерева и результирующего порядка обхода.
9.6.13. Рекурсия без оптимизации
(Это упражнение требует доступа к компилятору, например, С или С++, с поддержкой оператора goto)
Реализуйте и протестируйте прямую итеративную трансляцию процедуры hanoi в ее начальном варианте, используя goto и стек без оптимизации.
9.6.14. Сохранение стека сохранения
- Реализуйте и протестируйте итеративную, без goto, основанную на стеке версию Ханойской башни.
- Улучшьте решение, используя оптимизацию, основанную на хвостовой рекурсии, избегая во втором вызове ненужного сохранения данных.
- При условии, что выполнено предыдущее упражнение, примените ту же оптимизацию к версии с goto.
9.6.15. Обход без стека
Мы видели, что реализация рекурсии требует обращения преобразования аргументов рекурсивного вызова. Стек является одним из возможных путей решения этого требования. Используя подходящие приемы обращения, реализуйте обход бинарного дерева, например, в инфиксном порядке, без рекурсии и без стека, за исключением, возможно, стека булевских значений (или, эквивалентно, бита в каждом узле).
Подсказка: временно переопределите связи дерева, сохраняя информацию о том, откуда пришли в узел.
Контр-подсказка: решение можно найти, набрав при поиске в Интернете слова Deutsch, Shorr или Waite (имена авторов известного алгоритма, основанного на этой идее). Не делайте этого! Спроектируйте алгоритм самостоятельно, затем посмотрите ссылки, если пожелаете.
9.6.16. Транзитивное замыкание
(Это упражнение ссылается на последнюю лекцию)
Сформулируйте определение транзитивного замыкания как рекурсивное определение.
9.6.17. Матричная алгебра для продукций БНФ
(Это упражнение требует знания основ линейной алгебры)
Рассмотрим БНФ-продукции – небольшой пример из этой лекции или более расширенный из предыдущих лекций, включающий только продукции для конкатенации и выбора (без повторения, поскольку оно может быть заменено комбинацией двух других).
- Рассматривайте конкатенацию лексем как "умножение", а альтернативный выбор – как "сложение". Покажите, что в этом случае возможно выразить грамматику как матричное уравнение
 , где
, где  – это вектор нетерминалов,
– это вектор нетерминалов,  – матрица из терминалов и нетерминалов, и B является вектором.
– матрица из терминалов и нетерминалов, и B является вектором. - Обсудите пути решения такого уравнения, следуя модели, предложенной для уравнения неподвижной точки.