Списки
6.2. Связные списки
Мы уже познакомились с базисными свойствами и методами списков, независимо от того, как они реализованы. Займемся теперь вариантами, начав с важного частного случая связного списка, с класса LINKED_LIST.
Основы связных списков
При работе со станциями метро мы познакомились с приемами связывания элементов в последовательную структуру:
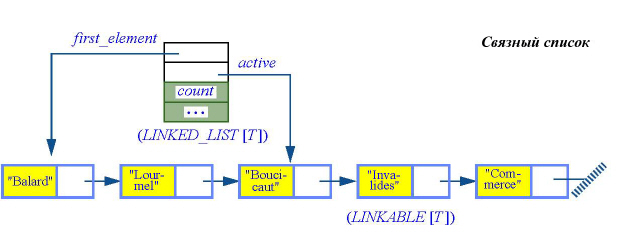
Теперь, благодаря механизму универсализации, возможно обобщение на произвольные структуры. Экземпляр LINKED_LIST[T] для некоторого типа T будет ссылаться на ноль или более связанных ячеек, принадлежащих классу LINKABLE[T]. Каждый экземпляр класса LINKABLE[T] содержит значение типа T и ссылку на другой экземпляр этого класса:
Как показано на рисунке, реализация включает два класса.
- Верхний объект является экземпляром LINKED_LIST[T]. Такой объект называют заголовком списка – он содержит общую информацию о списке и обеспечивает доступ к элементам списка, но сам он не представляет никакого элемента. Поле count задает число элементов. Оно реализовано атрибутом (но могло быть также и функцией). Другие поля являются ссылками на ячейки списка. Атрибут first_element задает ссылку, ведущую к первой ячейке, active – ведет к ячейке в позиции курсора.
- Другие объекты представляют ячейки списка; они являются экземплярами класса LINKABLE, также универсального, с тем же родовым параметром, задающим тип элементов списка – LINKABLE[T].
При нормальном использовании клиентскому приложению требуется только класс LINKED_LIST. Класс LINKABLE необходим для реализации, представляя очень простое понятие ячейки списка, которая может быть связана с другой подобной ячейкой: типичный экземпляр выглядит следующим образом:
Реализация методов класса LINKED_LIST основана на запросах класса LINKABLE и связанных сеттер-командах:
item: G
— Значение в ячейке.
right: LINKABLE [G ]
— Следующий элемент.
put (x): G
— Установить значение элемента равным x.
ensure
set: item = x
put_right (other: LINKABLE [G])
— Связывание с ячейкой other.
ensure
set: right = other
Вставка и удаление
Следующий рисунок показывает, как класс LINKED_LIST реализует команду put_right, которая должна добавлять элемент справа от курсора, не перемещая сам курсор. Для связного списка достаточно создать новую ячейку LINKABLE и обновить ссылки:
Реализация метода использует два вызова put_right из класса LINKABLE. Обратите внимание также на то, что требуется особый разбор случая, когда список пуст и before истинно:
put_right (v: G)
— Добавить v справа от позиции курсора, не меняя его положения.
require
not_after: not after
local
p: LINKABLE [G ] — Ячейка должна быть создана
do
create p.make (v)
if before then — Специальный случай before:
p.put_right ( first_element)
first_element:= p
active:= p
else — Общий случай:
p.put_right (active.right)
active.put_right ( p)
end
ensure
next_exists: active.right /= Void
inserted: (not old before) implies active.right.item = v
inserted_before: (old before) implies active.item = v
end
В данном примере мы манипулируем со ссылками. Он еще раз демонстрирует, как необходимо проявлять аккуратность при проведении этих операций. Даже здесь, когда выполняются простые операции, алгоритм требует особого внимания, чтобы убедиться, что он корректно работает во всех ситуациях. Трудности возрастают в следующих двух примерах – удаления элемента и обращения списка.
Процедура remove удаляет ячейку списка в позиции курсора. Спецификация, заданная ранее, устанавливает, что курсор передвигается в следующую позицию, непосредственно справа от той, где он находился, что показана на следующем далее рисунке. Реализация должна изменить две ссылки.
- Необходимо изменить ссылку right у ячейки, непосредственно предшествующей курсору (у элемента со значением "Lourmel"), чтобы обойти удаляемый элемент.
- Обновить в соответствии с требованиями позицию курсора, для чего следует изменить ссылку active объекта LINKED_LIST (здесь элемент "Invalides").
Для изучения текста процедуры следует обратиться к фактической реализации – процедуре remove из класса LINKED_LIST. Она более сложная, чем put_right, поскольку необходимо учитывать больше специальных случаев, в частности, когда курсор установлен на первом или последнем элементе. Целесообразно вначале разобрать текст более простой процедуры – remove_right.
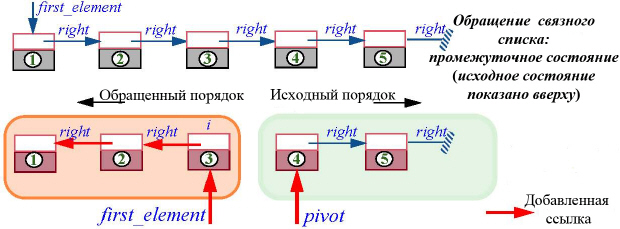
Обращение связного списка
В качестве заключительной иллюстрации алгоритмов, манипулирующих ссылками, рассмотрим метод, единственный в этой лекции, не включенный в момент написания этого текста в состав соответствующего класса LINKED_LIST библиотеки EiffelBase (нет никаких объективных причин, чтобы не сделать это теперь). Мы хотим создать процедуру, обращающую элементы списка. Основная идея ясна, поскольку мы уже писали функцию, решающую эту задачу. Теперь мы должны справиться с двумя дополнительными проблемами: обобщением на произвольные связные списки и необходимостью обращения существующего списка на том же месте, что делает нашу задачу более сложной.
Прежде всего заметим, как не следует решать задачу. Корректный, но неэффективный алгоритм может быть следующим. Вначале нужно перейти к последнему элементу, связать с ним first_element-ссылку, а сам элемент связать с его левым соседом. Затем повторять эти действия, проходя каждый раз с левого конца по ссылкам до достижения обращенной части списка. При этом понадобятся две локальные переменные, одна будет хранить старое значение first_element, чтобы можно было выполнить проход по списку, вторая будет хранить ссылку на левого соседа, необходимую для обращения текущего элемента.
Время программирования!
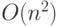
Превратите приведенное неформальное описание в процедуру и испытайте ее на некотором списке целых. Организуйте код так, чтобы подсчитывалось число итераций цикла.
class MY_INTEGER_LIST inherit LINKED_LIST [INTEGER] feature
reverse do … Разместите здесь Ваш код … end
end
Нет необходимости изменять другие свойства родительского класса.
Проблема такого подхода связана с его эффективностью: первый проход по списку потребует count итераций, второй count – 1, третий count – 2 и т.д., так что общее число итераций равно count (count + 1) / 2, что означает  . Мы же хотим иметь алгоритм со сложностью O(count). Начнем его проектировать. Он начинается так же, как и версия для функции с единственным циклом, но изменяет структуру цикла на месте, не создавая нового списка:
. Мы же хотим иметь алгоритм со сложностью O(count). Начнем его проектировать. Он начинается так же, как и версия для функции с единственным циклом, но изменяет структуру цикла на месте, не создавая нового списка:
В этом промежуточном состоянии:
- first_element присоединен к одному из элементов исходного списка (как на рисунке) или имеет значение void;
- мы полагаем, что first_element всегда представляет позицию i в исходном списке: позицию элемента или, если first_element является void, позицию слева от первого элемента при условии его существования (это также означает, что для пустого списка – помните о проверке граничных условий! – first_element является void);
- pivot присоединен к элементу, который был непосредственным правым соседом элемента i в исходном списке. Согласно правилам, pivot есть void, если и только если либо i был последним элементом исходного списка, либо список пуст;
- начиная с pivot и следуя right-ссылкам, представлен список, который составлен из всех элементов исходного списка, следующих за элементом i, если они есть в их исходном порядке;
- начиная с first_element и следуя right, представлен список, который составлен из всех элементов исходного списка, предшествующих, а также включая элемент i, если таковые есть в их обращенном порядке.
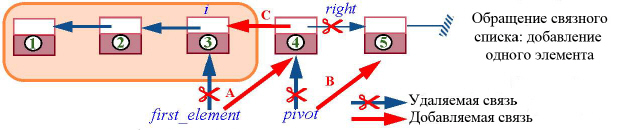
Здесь присутствуют все признаки хорошего инварианта итеративного процесса, где процесс может рассматриваться как последовательная аппроксимация. Достаточно тривиально обеспечить начальную истинность инварианта, установив pivot как исходный first_element и first_element – void. Инвариант вырабатывает желаемый результат по завершении, когда i является последней позицией исходного списка, first_element даст нам полностью обращенный список! Когда же инвариант выполняется в промежуточном состоянии, то несложно расширить его на следующий элемент списка, изменяя значение трех ссылок, как показано на следующем рисунке:
Код такой итерации цикла достаточно прост:
i:=first_element
first_element:= pivot — Операция, помеченная А на рисунке
pivot:= pivot.right — Операция В
first_element.put_right (i) — Операция С
Заметьте необходимость временной переменной i для записи исходного значения first_element, так, чтобы мы могли связать новый первый элемент в последней операции С.
Приведем полный алгоритм, соединяя все вместе. Для выражения варианта – следует заботиться о завершаемости цикла – добавим целочисленную переменную с, подсчитывающую итерации, или, что то же, записывающую позицию текущего first_element.
reverse
— Изменить связи элементов в обратном порядке.
— (Нет предусловия – будет работать и для пустого списка.)
— Не перемещает курсор.
local
pivot, i: LINKABLE [G ] ; c: INTEGER
do
from
pivot:= first_element ; first_element:= Void ; c:= 0
invariant
— с – индекс элемента first_element, если он есть в исходном списке;
— список, начинающийся с first_element, включает все элементы
— в обращенном порядке вплоть до позиции с в исходном списке;
— список, начинающийся с pivot, включает все элементы в исходном
—порядке, начиная с позиции с.
until
pivot = Void
loop
i:= first_element
first_element:= pivot
pivot:= pivot.right
first_element.put_right (i)
c:= c + 1
variant
count – c + 1
end
end
Убедитесь, что вы хорошо понимаете алгоритмы reverse и put_right, поскольку они демонстрируют основные идеи реализации операций над связными списками. Они также демонстрируют трудности, возникающие при работе со ссылками, и напоминают о принципе программирования ссылок – такие операции должны быть частью специальных, тщательно спроектированных кластеров или частью профессиональных библиотек общецелевого назначения, но не должны быть частью приложения, реализующего "бизнес-логику" программы.
Производительность операций над связным списком
Можно оценить стоимость операций над связным списком.
- Операции, для которых нужно выполнять действия в позиции курсора, – put_right и remove_right – имеют сложность O(1).
- Операции, которым необходим проход по списку, имеют сложность O(count). К таким операциям относятся независимо от реализации search и has. Процедура reverse, как мы видели, также имеет сложность O(count). Такую же сложность имеет и операция по перемещению курсора – go_i_th, а также finish, реализованная как go_i_th (count).
Интересный случай представляет операция extend, добавляющая элемент в конец списка. Как отмечалось, она может быть реализована через операцию finish, за которой следует операция put_right и go_i_th, если требуется восстановить позицию курсора. Поэтому суммарная сложность операции есть O(count). Часто при создании списка приходится поочередно добавлять новые элементы в конец списка. В этом случае позволительно оставлять курсор в конце списка, тогда для реализации extend нужно выполнить операции put_right и forth, что дает сложность O(1).
Некоторые операции, работающие в позиции курсора, более хитро устроены, чем put_right и remove_right: им может, например, понадобиться ссылка на элемент, стоящий слева от курсора. Таковой является операция remove, удаляющая элемент под курсором. Включение атрибута previous, указывающего на левого соседа, позволяет сохранить сложность O(1) для таких операций, но несколько снижает эффективность других операций, поскольку требует обновления атрибута при выполнении ряда действий.
Интерфейс LINKED_LIST и других списковых классов не делает очевидного различия между forth, передвигающим курсор на одну позицию вправо, и back, двигающим курсор в обратном направлении. Однако производительность этих операций кардинально отличается: forth – O(1), в то время как back имеет сложность O(count), будучи реализована как
start
go_i_th (index – 1)
При добавленном атрибуте previous сохраняется сложность O(1), но только при однократном выполнении back, так что в общем случае введение этого атрибута мало чем помогает в эффективности этой операции. Симметричные структуры, такие как двусвязные списки TWO_WAY_LIST, рассматриваемые ниже, устраняют эти трудности.
Дадим обзор сложности выполняемых операций. Вначале рассмотрим операции вставки удаления.
| Операции | Методы в классе LINKED_LIST | Сложность | Комментарий |
|---|---|---|---|
| Вставка в позицию курсора | put_right, put_left | O(1) | Для операции слева от курсора сложность О(1) требует атрибута previous |
| Удаление в позиции курсора | remove_right, remove | O(1) | remove_left имеет сложность O(count) |
| Вставка в конец, если курсор находится уже там | extend | O(1) |
Сложность операций по изменению позиции курсора:
| Операции | Методы в классе LINKED_LIST | Сложность | Комментарий |
|---|---|---|---|
| Передвинуть курсор к первому элементу | start | O(1) | |
| Передвинуть курсор к последнему элементу | finish | O(count) | |
| Передвинуть курсор на шаг вправо | forth | O(1) | |
| Передвинуть курсор на шаг влево | back | O(count) |
Глобальные операции могут требовать прохода по списку:

![Экземпляр LINKABLE[T]](/EDI/16_03_16_5/1458080524-15795/tutorial/1000/objects/6/files/04_16.jpg)