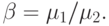|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Приложение А
Упражнение 14.2. Сеть очередей
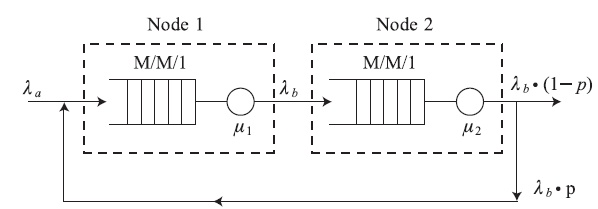
Мы рассматриваем следующую открытую сеть очередей:
Сеть очередей состоит из двух узлов, оба имеют дисциплину обслуживания типа 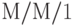 . Заявки от клиентов прибывают извне согласно Пуассоновскому процессу с интенсивностью
. Заявки от клиентов прибывают извне согласно Пуассоновскому процессу с интенсивностью  вызова в единицу времени и экспоненциально распределенным временем обслуживания со средней величиной
вызова в единицу времени и экспоненциально распределенным временем обслуживания со средней величиной 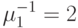 единицы времени, и соответственно
единицы времени, и соответственно 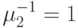 единицы времени. Вероятность
единицы времени. Вероятность  , с которой заявка от клиента, будучи обслужена во втором узле, вернется к первому узлу, равна
, с которой заявка от клиента, будучи обслужена во втором узле, вернется к первому узлу, равна 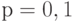 ,, и
,, и 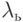 - полная интенсивность прибытия к каждому из этих двух узлов.
- полная интенсивность прибытия к каждому из этих двух узлов.
- Найти согласно предположению о статистическом равновесии (используя уравнения равновесия потока) предложенную нагрузку каждому из этих двух узлов.
-
Какой интервал является
 -ограниченным, если система находится в статистическом равновесии?
-ограниченным, если система находится в статистическом равновесии?Далее мы принимаем, что предложенная нагрузка к первому узлу и соответственно узлу два, является 0.8 Эрл и соответственно 0.4 Эрл.
- Принять статистическое равновесие и форму записи вероятности состояния, при который
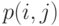 обозначает вероятность, что обслуживается
обозначает вероятность, что обслуживается  заявок от клиентов в первом узле и
заявок от клиентов в первом узле и  заявок от клиентов в втором узле. (Используйте решение мультипликативной формы
заявок от клиентов в втором узле. (Используйте решение мультипликативной формы 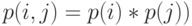 .
. - Рассмотрим теперь закрытую сеть очередей (например, предполагая, что
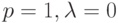 ). Мы рассматриваем случай
). Мы рассматриваем случай 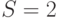 клиента. Вычислите использование этих двух узлов (обслуженная нагрузка), представляя эту систему как централизованную систему организации очереди обслуживающего прибора (используйте алгоритм свертывания).
клиента. Вычислите использование этих двух узлов (обслуженная нагрузка), представляя эту систему как централизованную систему организации очереди обслуживающего прибора (используйте алгоритм свертывания). - Фиксированное число клиентов
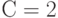 соответствует тому, что мы находимся на диагонали
соответствует тому, что мы находимся на диагонали 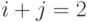 в вопросе 3. Показать, что при нормализации вероятностей состояний, при условии, что мы находимся на диагонали, использование будет такое же, как и в вопросе 4.
в вопросе 3. Показать, что при нормализации вероятностей состояний, при условии, что мы находимся на диагонали, использование будет такое же, как и в вопросе 4. -
Мы рассматриваем снова ту же самую открытую сеть организации очередей, как в вопросах 1-3. Создайте двухмерную диаграмму переходов состояний сети организации очереди, где мы имеем следующие переходы состояния:
- заявка от клиента прибывает извне,
- заявка от клиента передается от узла 1 к узлу 2,
- заявка от клиента передается от узла 2 к узлу 1,
- заявка от клиента поступает от системы. Действительно ли диаграмма переходов состояний обратима?
Упражнение 14.5. Закрытая сеть очередей
Рассмотрим закрытую сеть очередей с 2 узлами и одним обслуживающим прибором с дисциплиной типа 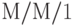 . После окончания обслуживания в узле заявку от клиента передают другому узлу. В сети организации очередей общее количество заявок от клиентов -
. После окончания обслуживания в узле заявку от клиента передают другому узлу. В сети организации очередей общее количество заявок от клиентов -  . Скорости обслуживания (интенсивность) в узле 1 и 2 -
. Скорости обслуживания (интенсивность) в узле 1 и 2 - 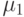 и
и 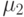 соответственно.
соответственно.
Предложим, что система находится в статистическом равновесии. Состояние системы,  определяется числом клиентов в узле 1 (тогда во втором узле будет
определяется числом клиентов в узле 1 (тогда во втором узле будет 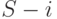 клиентов).
клиентов).
- Создать одномерную диаграмму переходов состояний системы.
- Найти вероятности состояния системы и среднее число клиентов в этих двух узлах.
- Найти из вероятностей состояния интенсивность
 , с которой клиенты циркулируют в системе, и использовать это, чтобы найти время цикла заявки клиента (принять дисциплину организации очереди FCFS ).
, с которой клиенты циркулируют в системе, и использовать это, чтобы найти время цикла заявки клиента (принять дисциплину организации очереди FCFS ). - Каковы отношения между средними временами пребывания (время пребывания = время ожидания + время обслуживания) в этих двух узлах? (Примените формулу Литтла).
- Далее надо принять, что
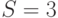 клиента,
клиента, 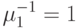 единице времени,
единице времени, 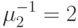 единицы времени.
единицы времени. - Применить алгоритм свертывания, чтобы найти вероятности состояния системы, и вычислить среднее число клиентов в этих двух узлах.
- Применить алгоритм MVA, чтобы найти среднее число клиентов в обоих узлах.
Упражнение 14.6. Модель восстановления машин как циклическая сеть очередей
Мы рассматриваем модель восстановления машин с 4 клиентами (источники, терминалы). Заявки от клиентов имеют экспоненциально распределенные времена раздумья клиентов с интенсивностью обслуживания 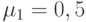 в единицу времени ( узел 1 ). Заявки обслуживаются последовательно единственным обслуживающим прибором. Заявка сначала обслуживается в узле 2, который является единственным обслуживающим прибором с экспоненциально распределенными временами обслуживания со средней величиной
в единицу времени ( узел 1 ). Заявки обслуживаются последовательно единственным обслуживающим прибором. Заявка сначала обслуживается в узле 2, который является единственным обслуживающим прибором с экспоненциально распределенными временами обслуживания со средней величиной 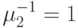 единицы времени. Затем заявка от клиента поступает к узлу 3, который является единственным обслуживающим прибором с экспоненциально распределенными временами обслуживания со средней величиной
единицы времени. Затем заявка от клиента поступает к узлу 3, который является единственным обслуживающим прибором с экспоненциально распределенными временами обслуживания со средней величиной 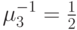 единицы времени. После окончания обслуживания в узле 3 заявка от клиента возвращаются к узлу 1, и запускается новое время раздумья.
единицы времени. После окончания обслуживания в узле 3 заявка от клиента возвращаются к узлу 1, и запускается новое время раздумья.
Эта система - единственная цепная циклическая сеть организации очереди с 3 узлами и 4 идентичными источниками. Узел 1 (терминалы) соответствует 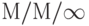 системе организации очереди тогда, как и узел 2, и узел 3 -
системе организации очереди тогда, как и узел 2, и узел 3 - 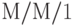 -системы с одним обслуживающим прибором. Заявки от клиентов циркулируют между узлами в циклической последовательности 1,2,3, 1,2,…….
-системы с одним обслуживающим прибором. Заявки от клиентов циркулируют между узлами в циклической последовательности 1,2,3, 1,2,…….
- Предположить, что нагрузка узла 3 равна единице, и найти относительные нагрузки узла 1 и узла 2.
- Найти вероятность относительного состояния каждого узла, отдельно.
- Применить алгоритм свертывания, чтобы найти абсолютные вероятности состояния каждого узла.
- Найти среднее число заявок от клиентов на каждом узле.
- Найти среднее время пребывания (ожидание + обслуживание) для заявки от клиента на каждом узле и среднего полного времени цикла.
- Найти среднюю длину очереди для заявки клиента на трех узлах, если мы увеличим число заявок от клиентов с 4 до 5.
Упражнение 14.7. Сеть очередей в соответствии с моделью Энгсета
Рассмотрим систему с потерями Энгсета с 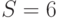 источниками и
источниками и 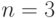 каналами. Интенсивность поступления вызовов от свободного источника
каналами. Интенсивность поступления вызовов от свободного источника 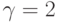 вызова в единицу времени и среднее время обслуживания
вызова в единицу времени и среднее время обслуживания 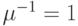 (выбрано как единица времени).
(выбрано как единица времени).
- Найти предложенную нагрузку.
-
Вычислить потери по времени
 , используя формулу, рекурсивную по
, используя формулу, рекурсивную по  . Показать каждый шаг в рекурсии.
. Показать каждый шаг в рекурсии.Рассмотрим закрытую сеть очередей с
 узлами и
узлами и 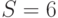 клиентами. Каждый узел имеет бесконечное число мест ожидания и скорость обслуживания
клиентами. Каждый узел имеет бесконечное число мест ожидания и скорость обслуживания 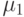 на один обслуживающий прибор.
на один обслуживающий прибор.Второй узел -
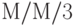 -система с потерями со скоростью обслуживания
-система с потерями со скоростью обслуживания 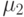 на один обслуживающий прибор, соответствует бесконечному обслуживающему прибору, усеченному в состоянии 3.
на один обслуживающий прибор, соответствует бесконечному обслуживающему прибору, усеченному в состоянии 3.Маршрутизация является циклической - такой, что клиент, обслуженный в первом узле, переходит во второй узел а клиент, обслуженный во втором узле, переходит на обслуживание в первый узел. Клиент, получивший отказ во втором узле, возвращается в первый узел (то есть остается). Предположим, что скорость циркуляции -
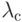 , и обозначим
, и обозначим 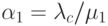 и
и 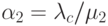 . Это сеть очередей с блокировкой, она имеет описание в форме произведения.
. Это сеть очередей с блокировкой, она имеет описание в форме произведения. - Найти вероятность относительного состояния каждого узла как независимой системы.
- Свернуть эти два узла в один согласно предположению, что общее число клиентов 6, и показать, что вероятности состояний
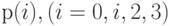 второго узла соответствуют системе с потерями Энгсета с
второго узла соответствуют системе с потерями Энгсета с 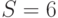 источниками,
источниками, 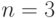 каналами и
каналами и