|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Приложение А
Упражнение 8.12. Энгсетовская модель с неоднородными источниками
Мы рассматриваем полную доступную Энгсетовская систему с потерями с 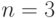 канала. На систему поступает предложенная нагрузка от
канала. На систему поступает предложенная нагрузка от 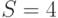 источников. Интенсивность поступления от свободного источника -
источников. Интенсивность поступления от свободного источника - 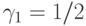 попыток вызова в единицу времени. Среднее время пребывания в системе выбрано как единица времени (
попыток вызова в единицу времени. Среднее время пребывания в системе выбрано как единица времени ( 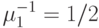 ). Все временные интервалы являются экспоненциально распределенными. Состояние системы определено как число занятых каналов, и каждый занятый источник занимает один канал.
). Все временные интервалы являются экспоненциально распределенными. Состояние системы определено как число занятых каналов, и каждый занятый источник занимает один канал.
- Найти предложенную нагрузку.
- Найти вероятности состояния системы при свертывании вероятности состояния 4 отдельных источников, при усечении до 3 каналов и при нормализации.
-
Найти потери по времени
 , потери по вызовам
, потери по вызовам  и потери по нагрузке
и потери по нагрузке  .
.Дополним источник, отличающийся от вышеупомянутого источника. Этот источник имеет интенсивность в свободное время, и интенсивность обслуживания в системе равные одной единице времени (
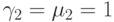 ). Источник, когда он занят, использует только один канал.
). Источник, когда он занят, использует только один канал. - Найти потери по времени для обоих источников их сверткой с вышеупомянутой системой типы вызовов.
- Найти потери по вызовам для обоих типов вызовов, применяя теорему прибытия.
- Найти потери по нагрузке для обоих типов источников, рассматривая отдельные элементы в течение свертывания (используя двухмерную диаграмму переходов состояний).
Упражнение 9.8. Система перегрузки, моделируемая прерванным пуассоновским процессом
Мы рассматриваем систему перегрузки, состоящую из первичной группы с одним каналом и группы перегрузки также с одним каналом ( Brockmeyer -система).
Прерывистый Пуассоновский процесс может описать процесс поступления вызовов к группе перегрузки.
-
Найти параметры для этого процесса перегрузки:
- интенсивность вызова
 );
); - интенсивность для ON периодов (
 );
); - интенсивность для OFF периодов (
 ).
).
- интенсивность вызова
- Создать диаграмму переходов состояний для группы перегрузки. Состояние системы перегрузки описано
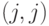 , где
, где  - число занятых каналов (
- число занятых каналов ( 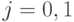 ) и
) и  - состояние прерванного Пуассоновского процесса
- состояние прерванного Пуассоновского процесса 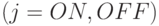 .
. -
Показать, что вероятности состояний дают:
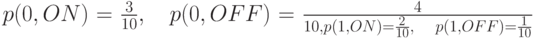 .
. -
Вычислить потери по времени и потери по вызовам для:
- только для системы перегрузки,
- всей системы.
Сравните последний результат с перегрузкой, полученной согласно В-формуле Эрланга.
- Найти потери по нагрузке для группы перегрузки
Упражнение 9.14. Система с потерями и потерями по нагрузке
Мы рассматриваем полнодоступную систему с потерями, имеющую 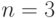 канала. На систему поступает нагрузка Паскаля, и в состоянии
канала. На систему поступает нагрузка Паскаля, и в состоянии  интенсивность поступления -
интенсивность поступления - 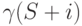 . Число источников -
. Число источников - 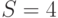 . Интенсивность поступления свободного источника -
. Интенсивность поступления свободного источника - 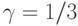 . Среднее время пребывания в системе выбрано как единица времени (
. Среднее время пребывания в системе выбрано как единица времени ( 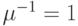 ).
).
Все временные интервалы являются экспоненциально распределенными. Состояние системы определяется как число занятых каналов.
Примечание: таблица В-формулы Эрланга для числа каналов от 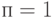 до 10 (с шагом = 1) и нагрузки А = 0 от 10 (с шагом = 0.25) приложена.
до 10 (с шагом = 1) и нагрузки А = 0 от 10 (с шагом = 0.25) приложена.
- Показать, что предложенная нагрузка - 2 [Эрл] и что пиковость - 1,5.
- Создать диаграмму переходов состояний и найти согласно предположению о статистическом равновесии вероятности состояние
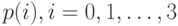 .
. - Найти потери по времени
 , потери по вызовам
, потери по вызовам  и потери по нагрузке
и потери по нагрузке  .
. - Вычислить перегрузку по нагрузке
 , используя метод Фредерикса-Хайварда (Frderiks-Hayward's).
, используя метод Фредерикса-Хайварда (Frderiks-Hayward's). - Вычислить потери по нагрузке
 , используя метод Сандера. Примите, что вышеупомянутая нагрузка - от системы с 4 каналами, которым предлагается 5 Эрл.
, используя метод Сандера. Примите, что вышеупомянутая нагрузка - от системы с 4 каналами, которым предлагается 5 Эрл. - Найти перегрузку по нагрузке
 , используя метод Вилкинсона-Бретшнайдера (Wilkinson-Bretschneider's) и метод ERT. Примите, что вышеупомянутая нагрузка - от системы с 4 каналами, которым предлагается 5 Эрл.
, используя метод Вилкинсона-Бретшнайдера (Wilkinson-Bretschneider's) и метод ERT. Примите, что вышеупомянутая нагрузка - от системы с 4 каналами, которым предлагается 5 Эрл.
Упражнение 10.1. Система с потерями с множественной доступностью
Мы рассматриваем систему с потерями с 3 идентичными серверами, обслуживающими два различных типа клиентов, заявки от которых прибывают согласно Пуассоновским процессам с интенсивностью:
тип 1: 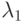 [заявок/единица времени],
[заявок/единица времени],
тип 2: 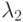 [заявок/единица времени].
[заявок/единица времени].
Оба типа заявок от клиентов имеют одинаковое экспоненциально распределенное распределение времени обслуживания со средней величиной 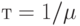 [единицы времени].
[единицы времени].
Клиенты типа 1 имеют полную доступность к трем обслуживающим приборам (серверам). Клиенты типа 2 блокированы, если во время прибытия заявок занят более чем один обслуживающий прибор.
Состояние системы определяется как общее количество обслуживаемых клиентов.
- Создать одномерную диаграмму переходов состояний для этой системы.
- Найти согласно предположению о статистическом равновесии вероятности состояний системы.
-
Найти выраженные с помощью вероятностей состояний потери по вызовам для клиентов типа 1 и типа 2.
Определим состояние системы как
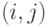 , где
, где  - число обслуживаемых заявок от клиентов типа 1 и
- число обслуживаемых заявок от клиентов типа 1 и  - число обслуживаемых заявок от клиентов типа 2.
- число обслуживаемых заявок от клиентов типа 2. - Создать двухмерную диаграмму переходов состояний для этой системы.
- Принять, что вероятности состояний известны, и найти нагрузку, которую обслуживают клиенты типа 2, когда обслуживается общее количество клиентов
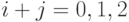 или
или  .
.
Упражнение 10.4. Системы с потерями со взаимной перегрузкой
Мы рассматриваем систему с потерями с двумя обслуживающими приборами. Вызовы прибывают согласно Пуассоновскому процессу с интенсивностью 20 вызовов в час. Время пребывания в системе экспоненциально распределенное, со средней величиной 180 секунд. Дать числовые ответы.
- Найти предложенную нагрузку.
-
Вычислить, используя рекурсивную формулу для В-формулы Эрланга, характеристики перегрузки системы (потери по времени равняется потерям по вызовам и потерям по нагрузке). Покажите отдельные шаги рекурсии.
Назовем вышеупомянутую систему подсистемой. Предположим теперь, что система состоит из двух подсистем вышеупомянутого типа (полная интенсивность поступления вызовов равняется 40 вызовам в час, имеется всего 4 полностью доступных обслуживающих прибора).
-
Создать одномерную диаграмму переходов состояний для полной системы и вычислить согласно предположению о статистическом равновесии вероятности состояния
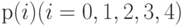 .
.Система работает следующим образом.
Для каждого вызова находят обслуживающий прибор в своей собственной подсистеме. Если оба обслуживающих прибора также заняты в этой системе, она блокируется. Состояние системы обозначается
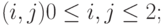
где
 и соответственно
и соответственно  обозначают число занятых обслуживающих приборов в подсистеме 1, соответственно в подсистеме 2.
обозначают число занятых обслуживающих приборов в подсистеме 1, соответственно в подсистеме 2. -
Создать двухмерную диаграмму переходов состояний для этой системы, используя следующие состояния.
Вычислить вероятности состояний двухмерной диаграммы переходов состояний, учитывая симметрию и используя объединенные вероятности состояний, рассчитанные в вопросе 3. (Все состояния в вопросе 5 с несколькими занятыми обслуживающими приборами, полученные в вопросе 3, объединены в единственное состояние).
Упражнение 10.7. Многомерная система с потерями
Мы рассматриваем полностью доступную систему с потерями с 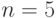 каналами, на которую поступают два потока нагрузки. Все процессы поступления вызовов и времена обслуживания имеют тип М. (Пуассоновский экспоненциальный) Все параметры приведены ниже в единицах времени:
каналами, на которую поступают два потока нагрузки. Все процессы поступления вызовов и времена обслуживания имеют тип М. (Пуассоновский экспоненциальный) Все параметры приведены ниже в единицах времени:
| Поток нагрузки 1: | Интенсивность поступления  , , |
Среднее время обслуживания 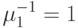 , , |
|
Каждый вызов требует 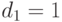 , сервера. , сервера. |
|
| Поток нагрузки 2: | Интенсивность прибытия 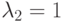 , , |
Среднее время обслуживания 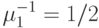 , , |
|
Каждый вызов требует 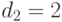 сервера. сервера. |
Если попытки вызова не могут быть обслужены при заданной пропускной способности во время их поступления, то это они теряются (Явные потери вызовов).
- Найти предложенную нагрузку для обоих потоков нагрузки, измеренную в числе каналов.
- Создать двухмерную диаграмму переходов состояний системы, где состояние
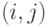 обозначает, что,
обозначает, что,  каналов, заняты вызовами, составляющими нагрузку типа 1 (
каналов, заняты вызовами, составляющими нагрузку типа 1 ( 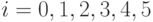 ), и у каналы заняты вызовами типа 2 (
), и у каналы заняты вызовами типа 2 ( 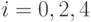 ), где мы имеем
), где мы имеем 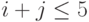 .
. -
Показать, что диаграмма переходов состояний обратима, и найти все вероятности состояний
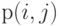 , выраженных через
, выраженных через  . Найдите потери по времени, потери по вызовам и потери по нагрузке для обоих потоков нагрузки.
. Найдите потери по времени, потери по вызовам и потери по нагрузке для обоих потоков нагрузки.Пусть
 , обозначают суммирование всего состояния, где общее количество занятых серверов:
, обозначают суммирование всего состояния, где общее количество занятых серверов: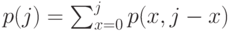
-
Показать, что следующая рекурсивная формула справедлива для системы, которую рассматривают:
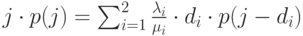 .
.
Упражнение 10.8. Система мобильной коммуникации с двумя типами нагрузки
Мобильная система связи с 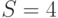 абонентами имеет доступ к
абонентами имеет доступ к 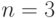 каналам. Все принятые вызовы занимают один канал в течение экспоненциально распределенного временного интервала со средней величиной
каналам. Все принятые вызовы занимают один канал в течение экспоненциально распределенного временного интервала со средней величиной 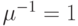 единицы времени. Система используется как система с потерями. Есть два процесса поступления вызовов:
единицы времени. Система используется как система с потерями. Есть два процесса поступления вызовов:
- исходящие вызовы, сгенерированные
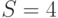 абонентами (нагрузка РСТ-П ). Свободный источник генерирует
абонентами (нагрузка РСТ-П ). Свободный источник генерирует 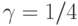 попыток вызова в единицу времени;
попыток вызова в единицу времени; - входящие вызовы, прибывающие согласно Пуассоновскому процессу с интенсивностью поступления
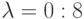 попыток вызова в единицу времени (нагрузка PCT-I ). Входящий вызов, который принят, занимает свободный канал и один из свободных источников, который таким образом становится занятым и не делает больше попыток вызова. Число занятых источников всегда равняется числу занятых каналов.
попыток вызова в единицу времени (нагрузка PCT-I ). Входящий вызов, который принят, занимает свободный канал и один из свободных источников, который таким образом становится занятым и не делает больше попыток вызова. Число занятых источников всегда равняется числу занятых каналов.
- Найти входящую предложенную нагрузку
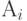 , исходящую
, исходящую  (предположите, что поток нагрузки, который рассматривают, является единственным).
(предположите, что поток нагрузки, который рассматривают, является единственным). - Создать одномерную диаграмму переходов состояний для системы, когда состояние системы определено как число занятых каналов. Найти вероятности состояния согласно предположению о статистическом равновесии.
- Найти потери по времени
 , потери по вызовам
, потери по вызовам  и потери по нагрузке
и потери по нагрузке  для обоих потоков нагрузки. (Потери по нагрузке для вызовов выхода получаются из полных потерь по нагрузке и известных потерь по нагрузке для входящих вызовов).
для обоих потоков нагрузки. (Потери по нагрузке для вызовов выхода получаются из полных потерь по нагрузке и известных потерь по нагрузке для входящих вызовов). - Показать, что диаграмма переходов состояний может интерпретироваться как диаграмма переходов состояний для единственного РСТ-II потока нагрузки, и найти эквивалентное число источников (не используя интеграл) и интенсивность поступления вызовов на один свободный источник.
- Пусть имеются различия между двумя типами нагрузки. Создайте двумерную диаграмму переходов состояний, где состояние системы
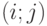 обозначает, что есть
обозначает, что есть  входящие вызов и
входящие вызов и  исходящих вызовов. Действительно ли диаграмма переходов состояний обратима?
исходящих вызовов. Действительно ли диаграмма переходов состояний обратима? - Найти потери по времени
 , потери по вызовам
, потери по вызовам  и потери по нагрузке
и потери по нагрузке  для обеих нагрузок потока, когда мы знаем вероятности состояния двухмерной диаграммы перехода состояний.
для обеих нагрузок потока, когда мы знаем вероятности состояния двухмерной диаграммы перехода состояний.
Упражнение 10.9. VoIP = Речь через интернет-протокол
Пояснения для ориентировки
Вокодеры (шифровальщики речи) выполняют алгоритм обработки речи. Для уменьшения необходимой пропускной способности используется датчик речевой активности, который указывает на перерывы речи и активные речевые периоды (всплеск пакетов). Постоянная скорость передачи информации в битах в течение периодов активности речи -  . Для некоторых известных шифровальщиков (как G.723 и G.729) применяется передача информации с постоянной скоростью
. Для некоторых известных шифровальщиков (как G.723 и G.729) применяется передача информации с постоянной скоростью  бит в течение периодов молчания, в период активности применяется скорость немного выше, чем
бит в течение периодов молчания, в период активности применяется скорость немного выше, чем 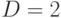 , для того, чтобы отобразить уровень фоновых шумов и другие параметры. Коэффициент активности речи - процент времени, когда вызов (абонент) находится в активном речевом состоянии. Это значение обычно приблизительно составляет 40 %. Для простоты мы выбираем следующие значения
, для того, чтобы отобразить уровень фоновых шумов и другие параметры. Коэффициент активности речи - процент времени, когда вызов (абонент) находится в активном речевом состоянии. Это значение обычно приблизительно составляет 40 %. Для простоты мы выбираем следующие значения 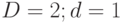 и коэффициент речевой активности = 0,5. Качество речи ухудшается больше чем на несколько процентов, если потеряны несколько всплесков.
и коэффициент речевой активности = 0,5. Качество речи ухудшается больше чем на несколько процентов, если потеряны несколько всплесков.
Задача
Мы рассматриваем систему с потерями с 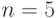 каналов. Попытки вызова поступают согласно Пуассоновскому процессу с интенсивностью
каналов. Попытки вызова поступают согласно Пуассоновскому процессу с интенсивностью 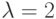 вызова в единицу времени. Предполагаем, что допустимо не более 4 одновременных вызовов в системе. Принятый вызов находится в одном из двух состояний: или состояние молчания, где задействован один канал, или активное состояние речи (всплеск разговора), где используется два канала (если это возможно). Принимаем, что вызов поступает в состоянии молчания (при прибытии нуждается в одном канале) и может закончиться только переходом в состояние тишины, то есть скорость обслуживания - 0 в активном речевом состоянии и
вызова в единицу времени. Предполагаем, что допустимо не более 4 одновременных вызовов в системе. Принятый вызов находится в одном из двух состояний: или состояние молчания, где задействован один канал, или активное состояние речи (всплеск разговора), где используется два канала (если это возможно). Принимаем, что вызов поступает в состоянии молчания (при прибытии нуждается в одном канале) и может закончиться только переходом в состояние тишины, то есть скорость обслуживания - 0 в активном речевом состоянии и  в состоянии молчания. (Все временные интервалы являются экспоненциально распределенными.) Каждое изменение вызова от молчания до активности речи (то есть начало всплеска разговора) происходит с той же скоростью 8, что и скорость изменения от активности речи до молчания (конец всплеска разговора). Если нет ни одного свободного канала, всплеск разговора теряется и вызов прибывает в состоянии молчания (потерянный всплеск разговора - модель с потерями, сравните с Энгсетовской моделью). В этой задаче скорость
в состоянии молчания. (Все временные интервалы являются экспоненциально распределенными.) Каждое изменение вызова от молчания до активности речи (то есть начало всплеска разговора) происходит с той же скоростью 8, что и скорость изменения от активности речи до молчания (конец всплеска разговора). Если нет ни одного свободного канала, всплеск разговора теряется и вызов прибывает в состоянии молчания (потерянный всплеск разговора - модель с потерями, сравните с Энгсетовской моделью). В этой задаче скорость  может быть выбрана произвольно так, например, можно выбрать
может быть выбрана произвольно так, например, можно выбрать 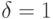 .
.
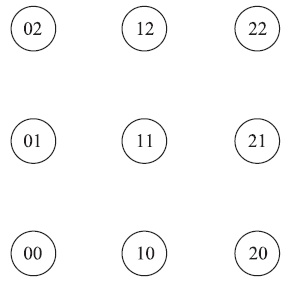
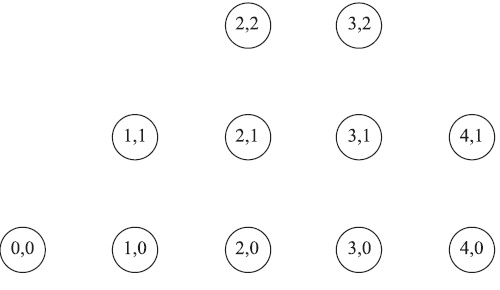
Мы определяем состояние системы как 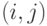 , где
, где 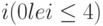 - число вызовов в системе, и
- число вызовов в системе, и 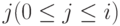 - число вызовов в состоянии "активная речь". Кроме того, мы имеем ограничение
- число вызовов в состоянии "активная речь". Кроме того, мы имеем ограничение 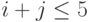 из-за общего количества каналов
из-за общего количества каналов 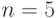 . Таким образом, получаем состояния, следующим образом используя рисунок, приведенный далее.
. Таким образом, получаем состояния, следующим образом используя рисунок, приведенный далее.
- Создать из данных состояний законченную диаграмму переходов состояний.
- Показать, что диаграмма переходов состояний обратима, и найти вероятности состояний согласно предположению о статистическом равновесии. Для проверки
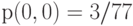 .
. - Составить уравнения равновесия узла для состояния (2,1). Найти (выраженные вероятностями состояний) потери по времени и потери по вызовам для новых попыток вызова.
-
Найти (выраженные вероятностями состояния) потери по времени и потери по вызовам для всплеска разговора.
Упражнение 12.16. Модель восстановления машин
Мы рассматриваем модель восстановления машин с 4 терминалами, имеющими экспоненциально распределенные времена раздумья с интенсивностью 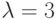 события в единицу времени. Два различных одиночных сервера обслуживают терминалы. С вероятностью Уз терминал нуждается в обслуживании от сервера 1, и с вероятностью 2/3 терминал нуждается в обслуживании от сервера 2. Сервер 1 имеет экспоненциально распределенное время обслуживания со средней величиной
события в единицу времени. Два различных одиночных сервера обслуживают терминалы. С вероятностью Уз терминал нуждается в обслуживании от сервера 1, и с вероятностью 2/3 терминал нуждается в обслуживании от сервера 2. Сервер 1 имеет экспоненциально распределенное время обслуживания со средней величиной 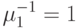 единица времени, и сервер 2 имеет экспоненциально распределенное время обслуживания со средней величиной
единица времени, и сервер 2 имеет экспоненциально распределенное время обслуживания со средней величиной 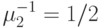 единицы времени. Терминал, обслуживаемый одним сервером, начинает новое время раздумья.
единицы времени. Терминал, обслуживаемый одним сервером, начинает новое время раздумья.
В модели восстановления машин есть два типа ошибок, каждая из которых нуждается в специализированном сервере.
- Найти для одного размышляющего терминала интенсивность поступления заявок на сервер 1 и сервер 2 соответственно.
- Создать диаграмму переходов состояний системы, когда мы определяем состояние системы
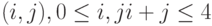 , где
, где  и, соответственно
и, соответственно  , число терминалов в сервере 1, соответственно в сервере 2.
, число терминалов в сервере 1, соответственно в сервере 2. - Показать, что диаграмма переходов состояний обратима.
- Найти вероятности состояния системы, когда система находится в статистическом равновесии.
- Найти использование (обслуженную нагрузку) двух одиночных серверов.
- Найти среднее время ожидания для терминала, который хочет обслуживаться в сервере 1.
Упражнение 12.17. Система с ограниченной очередью
Мы рассматриваем классическую систему организации очереди 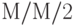 , которая имеет 2 обслуживающих прибора и 4 места ожидания так, чтобы самое большее в системе могли быть размещены заявки от 6 клиентов. Заявки от клиентов прибывают согласно Пуассоновскому процессу с интенсивностью
, которая имеет 2 обслуживающих прибора и 4 места ожидания так, чтобы самое большее в системе могли быть размещены заявки от 6 клиентов. Заявки от клиентов прибывают согласно Пуассоновскому процессу с интенсивностью  в единицу времени клиента, а времена пребывания в системе являются экспоненциально распределенными со средней величиной
в единицу времени клиента, а времена пребывания в системе являются экспоненциально распределенными со средней величиной 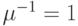 единице времени.
единице времени.
- Найти предложенную нагрузку.
-
Создать диаграмму переходов состояний для системы, где мы определяем состояние
 как общее количество клиентов в системе (либо находится на обслуживании, либо ожидает в очереди) (
как общее количество клиентов в системе (либо находится на обслуживании, либо ожидает в очереди) ( 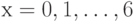 ). Найти вероятность того, что заявка: (а) будет обслужена немедленно, (b) будет обслужена после задержки, или (с) будет блокирована.
). Найти вероятность того, что заявка: (а) будет обслужена немедленно, (b) будет обслужена после задержки, или (с) будет блокирована.Разобьем систему на две идентичных подсистемы так, чтобы каждая подсистема имела один обслуживающий прибор и два места ожидания. Во время прибытия для заявки от клиента выбирается одна из этих двух систем с вероятностью, которая пропорциональна числу свободных позиций (обслуживающих приборов + места ожидания). Состояние системы определено как
 , где
, где  обозначает число заявок от клиентов в первой подсистеме и
обозначает число заявок от клиентов в первой подсистеме и  - число заявок от клиентов во второй подсистеме. Первая подсистема, таким образом, выбирается с вероятностью
- число заявок от клиентов во второй подсистеме. Первая подсистема, таким образом, выбирается с вероятностью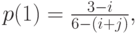
а вторая подсистема выбирается с вероятностью
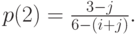
Когда для заявки клиента выбирают подсистему, он остается в этой подсистеме.
- Создать двухмерную диаграмму переходов состояний системы.
- Показать, что диаграмма переходов состояний обратима.
- Найти вероятности состояния.
- Найти вероятность, что заявка от клиента блокирована, и объяснить, почему она больше, чем вероятность, полученная в вопросе 2.