НОУ ИНТУИТ | Разработка телетрафика и планирование сетей. Лекция 5: Распределение моментов поступления вызовов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 20.04.2011 | Доступ: свободный | Студентов: 1059 / 208 | Оценка: 4.36 / 4.36 | Длительность: 22:21:00

Тема: Сетевые технологии

Специальности: Администратор коммуникационных систем, Архитектор программного обеспечения

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Крутые распределения

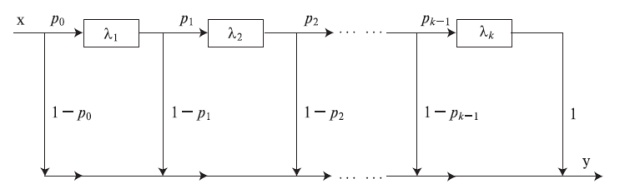
Крутые распределения также называют гиперэкспоненциальными распределениями или обобщенными распределениями Эрланга с коэффициентом формы в интервале $1 < \varepsilon \le 2$ . Эта обобщенная функция распределения получена свертыванием k экспоненциальных распределений (рис.4.2). Здесь мы рассматриваем только случай, где все k экспоненциальных распределений идентичны. Тогда мы получаем следующую плотность функция, которая называется k распределением Эрланга (распределение Эрланга k -го порядка):

$f(t)=\frac{(\lambda t)^{k-1}}{(k-1)!}*\lambda * e^{-\lambda t}, \lambda > 0, t \ge 0, k=1,2,\dots.$

( 4.8)

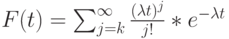$F(t)=\sum_{j=k}^{\infty} \frac{(\lambda t)^j}{j!}*e^{-\lambda t}$

( 4.9)

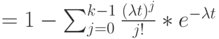$=1-\sum_{j=0}^{k-1} \frac{(\lambda t)^j}{j!}*e^{-\lambda t}$

( 4.10)

Следующие моменты могут быть найдены с использованием (3.31) и (3.32):

$m=\frac{k}{\lambda},$

( 4.11)

$\sigma^2=\frac{k}{\lambda^2},$

( 4.12)

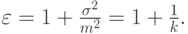$\varepsilon=1+\frac{\sigma^2}{m^2}=1+\frac 1k.$

( 4.13)

i -тый нецентральный момент:

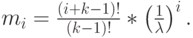$m_i=\frac{(i+k-1)!}{(k-1)!}*\left (\frac{1}{\lambda}\right )^i.$

( 4.14)

Функция плотности получена в секции 6.2.2. Средний остаток времени "жизни" 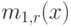$m_{1,r}(x)$ для $x \ge 0$ будет меньше, чем средняя величина:

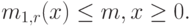
$m_{1,r}(x) \le m, x \ge 0.$

Рис. 4.3. k распределения Эрланга со средней величиной. Случай k = 1 соответствует экспоненциальному распределению (функции плотности)

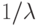С этим распределением мы имеем два параметра $(\lambda, k)$ , доступные для наблюдений. Средняя величина часто сохраняется фиксированной. Чтобы изучить влияние параметра k в функции распределения, мы нормализуем все k распределения Эрланга к одной и той же самой средней величине как 1, распределение Эрланга, то есть экспоненциальное распределение заменим средним значением $1/\lambda$ , a t -на k t или 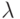$\lambda$ на $\lambda k$ :

$f(t)dt=\frac{(\lambda kt)^{k-1}}{(k-1)!}e^{-\lambda kt} k \lambda dt,$

( 4.15)

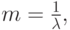$m=\frac{1}{\lambda},$

( 4.16)

$\sigma^2=\frac{1}{k \lambda^2},$

( 4.17)

$\varepsilon=1+\frac 1k.$

( 4.18)

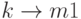Заметим, что коэффициент формы независим от времени. Функция (4.15) плотности проиллюстрирована на рис.4.3 для различных значений k с $\lambda =1$ . Возьмем случай, когда k = 1 соответствует экспоненциальному распределению. Если $k \to m1$ , мы получаем постоянный временной интервал ( 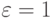$\varepsilon=1$ ). Решая f(t) = 0, находим максимальное значение:

$\lambda t=\frac{k-1}{k}$

( 4.19)

Так называемые крутые распределения носят такое имя, потому что увеличение функций распределения от 0 до 1 идет быстрее, чем в экспоненциальном распределении. В теории телетрафика мы иногда используем название - распределение Эрланга для усеченного Пуассоновского распределения (секция 7.3).

Плоские распределения

Общая функция распределения находится в этом случае с помощью взвешенной суммы экспоненциальных распределений (составное распределение) с коэффициентом формы $\varepsilon \ge 2$ :

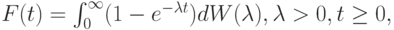$F(t)=\int_0^{\infty}(1-e^{-\lambda t})dW(\lambda), \lambda > 0, t \ge 0,$

( 4.20)

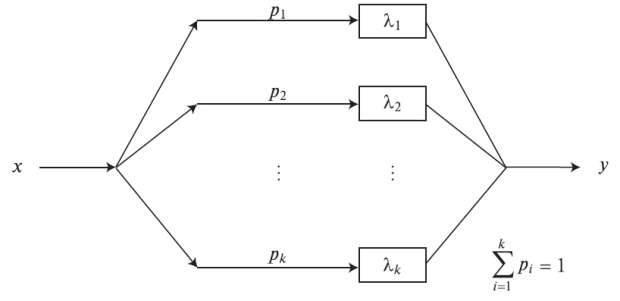
Функция веса может быть дискретна или непрерывна (интеграл Стилтьеса). Этот класс распределения соответствует параллельной комбинации экспоненциальных распределений (рис.4.4). Функция плотности называется полностью монотонной с чередующимися знаками (Пальма, 1957 [82]:

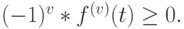$(-1)^v*f^{(v)}(t) \ge 0.$

( 4.21)

Среднее остаточное время "жизни" 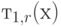$т_{1,r} (х)$ для всего $х \ge 0$ является большим, чем средняя величина:

$m_{1,r}(x) \ge 0, x \ge 0.$

( 4.22)

Рис. 4.4.

Комбинируя k экспоненциальных параллельных распределений и выбирая i - число ветви i с вероятностью 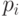p_i , мы получаем гиперэкспоненциальное распределение, которое является плоским распределением ( $\varepsilon \ge 2$ )

Гиперэкспоненциальное распределение

В этом случае $W(\lambda)$ - дискретно. Предположим, что нам даны следующие значения:

$\lambda_1, \lambda_2, \dots, \lambda_k,$

и что $W(\lambda)$ имеет положительные и увеличивающие значения:

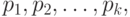
$p_1, p_2, \dots, p_k,$

где

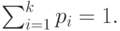$\sum_{i=1}^k p_i=1.$

( 4.23)

Для всех других значений $W(\lambda)$ является постоянным. В этом случае (4.20) становится:

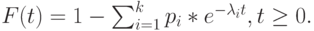$F(t)=1-\sum_{i=1}^k p_i*e^{-\lambda_it}, t \ge 0.$

( 4.24)

Средние величины и коэффициент формы могут быть найдены из (3.36)и(3.37)( $\sigma_i=m_{1,i}=1/\lambda$ ):

$m_1=\sum_{i=1}^k \frac{p_i}{\lambda_i},$

( 4.25)

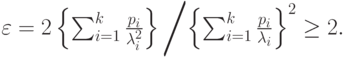$\varepsilon=2\left \{ \sum_{i=1}^k \frac{p_i}{\lambda_i^2}\right \} \left / \left \{ \sum_{i=1}^k \frac{p_i}{\lambda_i} \right \}^2 \ge 2.$

( 4.26)

Если k = 1 или все 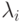$\lambda_i$ равны, мы получаем экспоненциальное распределение.

Распределения этого класса называются гиперэкспоненциальными распределениями, и могут быть получены комбинацией k параллельных экспоненциальных распределений, где вероятность выбора i -того распределения - 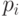p_i . Распределение называется плоским, потому что увеличения его функции распределения от 0 до 1 идет медленнее, чем при экспоненциальном распределении.

Практически, трудно оценить больше, чем один или два параметра. Самый важный случай - для n=2(p_1=p, p_2=1-p)

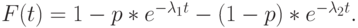$F(t)=1-p*e^{-\lambda_1 t}-(1-p)*e^{-\lambda_2 t}.$

( 4.27)

Статистические проблемы возникают, даже когда мы имеем дело с тремя параметрами. Так, для практических приложений, мы обычно выбираем 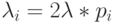$\lambda_i=2\lambda *p_i$ . и, таким образом, уменьшаем число параметров до двух.

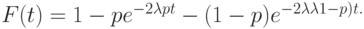$F(t)=1-pe^{-2\lambda pt}-(1-p)e^{-2\lambda \lambda 1-p)t.$

( 4.28)

Средняя величина и коэффициент формы получаются равными:

$m=\frac{1}{\lambda},\\ \varepsilon=\frac{1}{2p(1-p)}.$

( 4.29)

При таком выборе параметров две ветви имеют тот же самый вклад в среднюю величину. Pис.4.5 иллюстрирует пример.

Распределения Кокса

Комбинируя крутые и плоские распределения, мы получаем общий класс распределений (распределения фазового типа), которые может быть описаны с помощью экспоненциальной фазы в последовательном и параллельном случае (например, $k \times l$ матрицу). Чтобы проанализировать модель с таким видом распределений, мы можем применить теорию Марковских процессов, для которых имеются мощные инструментальные средства, такие, как метод диаграмм состояний (фазовый метод). В общем случае мы можем учесть обратную связь между состояниями (фазами).

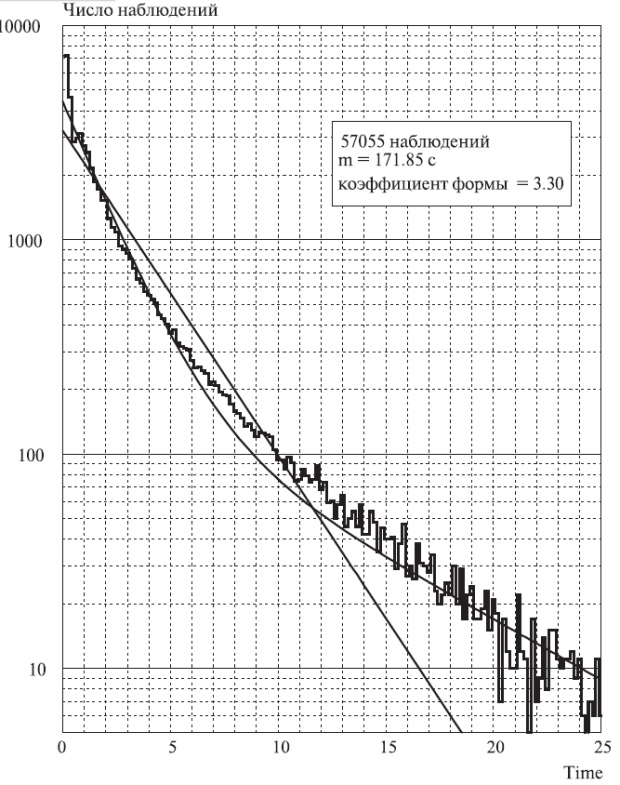
Рис. 4.5. Функция плотности (частотная) для времен пребывания в системе наблюдаемых линий на местной станции в течение часа наибольшей нагрузки.

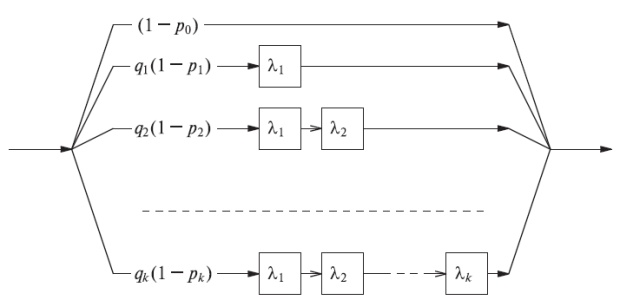
Рис. 4.6. Распределение Кокса - обобщенное распределение Эрланга, имеющее параллельные и последовательные экспоненциальные распределения.

Диаграмма состояния эквивалентна рис.4.7.

Рис. 4.7. Диаграмма состояний распределения Кокса (сравните с рис.4.6.)

Рассмотрим распределение Кокса, которое показано на рис.4.6 (Кокс, 1955 [17]). Оно также иногда называется распределением эрланговского разветвления (иначе, распределением Эрланга с ветвями).

Средняя величина и дисперсия этого распределения Кокса (рис.4.7) получаются из формулы в секции 3.2 для последовательных и параллельных случайных переменных, как это показано на рис.4.6:

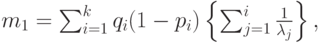$m_1=\sum_{i=1}^k q_i(1-p_i) \left \{ \sum_{j=1}^i \frac{1}{\lambda_j} \right \},$

( 4.30)

где

$q_i=p_0*p_1* \dots p_{i-1}.$

( 4.31)

Выражение q_i(1-p_i) - вероятность перехода процесса, когда он находится в i -том состоянии. Средняя величина может быть выражена простой формулой:

$m_1=\sum_{i=1}^k \frac{q_i}{\lambda_i}=\sum_{i=1}^k m_{1,i},$

( 4.32)

где $m_{1,i}=\frac{q_i}{\lambda_i}$ - средняя величина в i -том состоянии. Второй момент получается

$m_2=\sum_{i=1}^k\{q_i(1-p_i)*m_{2,i}\},\\ \quad=\sum_{i=1}^k\left\{ q_i(1-p_i)*\left \{\sum_{j=1}^i \frac{1}{\lambda_j^2}+\left ( \sum_{j=1}^i \frac{1}{\lambda_j}\right)^2 \right\} \right\},$

( 4.33)

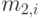где $m_{2,i}$ получен из (3.8): 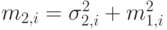$m_{2,i}=\sigma_{2,i}^2+m_{1,i}^2$ .; это можно записать как:

$m_2=2*\sum_{i=1}^k \left\{ \left(\sum_{j=1}^i \frac{1}{\lambda_j}\right)*\frac{q_i}{\lambda_i} \right \}.$

( 4.34)

После чего получаем дисперсию (3.8):

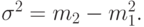
$\sigma^2=m_2-m_1^2.$

Сложение двух распределений Кокса для случайных переменных дает другое распределение Кокса для случайной переменной, то есть этот класс является замкнутым по отношению к сложению.

Функция распределения Кокса может быть записана как сумма экспоненциальных функций:

$1-F(t)=\sum_{i=1}^k c_i*e^{-\lambda_i t}.$

( 4.35)

где

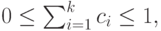
$0 \le \sum_{i=1}^k c_i \le 1,$

и

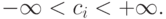
$- \infty < c_i < +\infty.$

Мультиноминальное распределение

Для более поздних приложений важны следующие свойства. Если мы полагаем, что точка выбрана наугад в пределах временного интервала, подчиняющегося распределению Кокса, то вероятность, что эта точка - в пределах фазы i, равна:

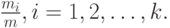$\frac{m_i}{m}, i=1,2,\dots, k.$

( 4.36)

Если мы повторяем этот эксперимент раз (независимо), то вероятность, что фаза наступала y_i раз, определяется с помощью мулътиноми-нальногораспределения (оно же - полиномиальное распределение):

$p\{y|y_1, y_2, \dots, y_k\}=\begin{pmatrix} y\\ y_1y_2 \dots y_k \end{pmatrix}*\left (\frac{m_{1,1}}{m}\right )^{y_1}*\left (\frac{m_{1,2}}{m} \right)^{y_2} \dots \left(\frac{m_{1,k}}{m} \right)^{y_k}.$

( 4.37)

где

$y=\sum_{i=1}^k y_i,$

и

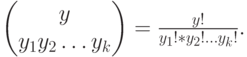$\begin{pmatrix} y\\ y_1y_2 \dots y_k \end{pmatrix}=\frac{y!}{y_1!* y_2! \dots y_k!}.$

( 4.38)

Элементы в (4.38) называются мультиноминальными коэффициентами. Благодаря свойству экспоненциальных распределений - отсутствию памяти, - мы имеем полную информацию об остаточном времени "жизни", если знаем номер текущей фазы.

Дальше >>

Авторизоваться

Разработка телетрафика и планирование сетей

Распределение моментов поступления вызовов

Крутые распределения

Плоские распределения

Гиперэкспоненциальное распределение

Распределения Кокса

Мультиноминальное распределение

Вопросы и ответы