|
Я завершила экзамен 90 баллов на 5. Сертификат не заказала. Сейчас пытаюсь найти как его заказать. у меня указано экзамен пройден баллы оценка видно, а чтоб заказать сертификат нигде не видно. |
Опубликован: 03.09.2010 | Доступ: свободный | Студентов: 3417 / 749 | Оценка: 4.11 / 3.69 | Длительность: 10:38:00
Тема: Программирование
Специальности: Программист, Архитектор программного обеспечения
Теги:
Лекция 5:
Работа с динамической памятью
Бинарные деревья
Бинарное дерево — это динамическая структура данных, состоящая из узлов, каждый из которых содержит кроме данных не более двух ссылок на различные бинарные деревья. На каждый узел имеется ровно одна ссылка. Начальный узел называется корнем дерева.
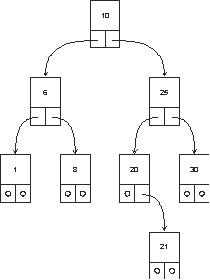
Пример бинарного дерева приведен на рис. 5.5 (корень обычно изображается сверху). Узел, не имеющий поддеревьев, называется листом. Исходящие узлы называются предками, входящие — потомками. Высота дерева определяется количеством уровней, на которых располагаются его узлы.
Если дерево организовано таким образом, что для каждого узла все ключи его левого поддерева меньше ключа этого узла, а все ключи его правого поддерева — больше, оно называется деревом поиска. Одинаковые ключи не допускаются. В дереве поиска можно найти элемент, двигаясь от корня и переходя на левое или правое поддерево в зависимости от значения ключа в каждом узле. Такой поиск гораздо эффективнее поиска по списку, поскольку время поиска определяется высотой дерева, а она пропорциональна двоичному логарифму количества узлов.
Дерево является рекурсивной структурой данных, поскольку каждое поддерево также является деревом. Действия с такими структурами изящнее всего описываются с помощью рекурсивных алгоритмов. Например, процедуру обхода всех узлов дерева можно в общем виде описать так:
procedure print_tree( дерево );
begin
print_tree( левое_поддерево )
посещение корня
print_tree( правое_поддерево )
end;Эта процедура позволяет получить последовательность ключей, отсортированную по возрастанию. Результат обхода дерева, изображенного на рис. 5.5:
1, 6, 8, 10, 20, 21, 25, 30
Если в функции обхода первое обращение идет к правому поддереву, результат обхода будет другим:
30, 25, 21, 20, 10, 8, 6, 1
Таким образом, деревья поиска можно применять для сортировки значений. При обходе дерева узлы не удаляются.
Для бинарных деревьев определены операции:
- включения узла в дерево;
- поиска по дереву;
- обхода дерева;
- удаления узла.
Для простоты будем рассматривать дерево, каждый элемент которого содержит только целочисленный ключ и два указателя.
type pnode = ^node;
node = record
data : word; { ключ }
left : pnode; { указатель на левое поддерево }
right : pnode { указатель на правое поддерево }
end;Доступ к дереву в программе осуществляется через указатель на его корень:
var root : pnode;
Рассмотрим сначала функцию поиска по дереву, так как она используется и при включении, и при удалении элемента ( пример 5.4).
function find(root : pnode; key : word; var p, parent : pnode) : boolean;
begin
p := root; { поиск начинается от корня }
while p <> nil do begin
if key = p^.data then { узел с таким ключом есть }
begin find := true; exit end;
parent := p; { запомнить указатель перед спуском }
if key < p^.data
then p := p^.left { спуститься влево }
else p := p^.right; { спуститься вправо }
end;
find := false;
end;
Листинг
5.4.
Функция поиска по бинарному дереву
Функция возвращает булевский признак успешности поиска. Ей передаются указатель на корень дерева, в котором выполняется поиск ( root ), и искомый ключ ( key ). Выходными параметрами функции являются указатели на найденный элемент ( p ) и его предка ( parent ).
Удаление элемента — более сложная задача, поскольку при этом необходимо сохранить свойства дерева поиска. Эта задача подробно описана в учебнике [ 10 ] .
В пример 5.5 приведен пример программы работы с бинарным деревом.
program bintree;
uses crt;
type pnode = ^node;
node = record
data : word; { ключ }
left : pnode; { указатель на левое поддерево }
right : pnode { указатель на правое поддерево }
end;
var root : pnode;
key : word;
option : word;
{ ------------------------------------ вывод дерева --------------------------- }
procedure print_tree(p : pnode; level : integer);
var i : integer;
begin
if p = nil then exit;
with p^ do begin
print_tree(right, level + 1);
for i := 1 to level do write(' ');
writeln(data);
print_tree(left, level + 1);
end
end;
{ ------------------------------- поиск по дереву – см. рис. 5.5----------- }
function find(root : pnode; key : word; var p, parent : pnode) : boolean;
{ ---------------------------- включение в дерево ----------------------------- }
procedure insert(var root : pnode; key : word);
var p, parent : pnode;
begin
if find(root, key, p, parent) then begin
writeln(' такой элемент уже есть'); exit; end;
new(p); { создание нового элемента }
p^.data := key;
p^.left := nil;
p^.right := nil;
if root = nil then root := p { первый элемент }
else { присоединение нового элемента к дереву}
if key < parent^.data
then parent^.left := p
else parent^.right := p;
end;
{ ------------------------------ удаление из дерева - см. учебник --------- }
procedure del(var root : pnode; key : word);
{ ------------------------------- главная программа --------------------------- }
begin
root := nil;
while true do begin
writeln('1 - вставка, 2 - удаление, 3 - вывод, 4 - выход');
readln(option);
case option of
1: begin { вставка }
writeln('Введите ключ для вставки: '); readln(key);
insert(root, key);
end;
2: begin { удаление }
writeln('Введите ключ для удаления: '); readln(key);
del(root, key);
end;
3: begin { вывод }
clrscr;
if root = nil then writeln ('дерево пустое')
else print_tree(root, 0);
end;
4: exit; { выход }
end;
writeln;
end
end.
Листинг
5.5.
Использование бинарного дерева
Рассмотрим функцию обхода дерева print_tree. Вторым параметром в нее передается целая переменная, определяющая, на каком уровне находится узел. Корень находится на уровне 0. Дерево печатается по горизонтали так, что корень находится слева. Для дерева, изображенного на рис. 5.5, вывод выглядит так:
30
25
21
20
10
8
6
1
София Шишова