Статистика нечисловых данных

Бинарные отношения. Пусть 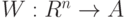- адекватный алгоритм в шкале наименований. Можно показать, что этот алгоритм задается некоторой функцией от матрицы 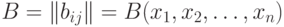где

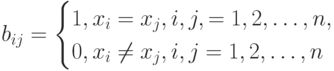
Если 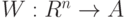- адекватный алгоритм в шкале порядка, то этот алгоритм задается некоторой функцией от матрицы 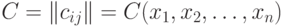порядка , где

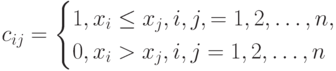
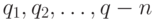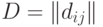Матрицы и можно проинтерпретировать в терминах бинарных отношений. Пусть некоторая характеристика измеряется у n объектов , причем - результат ее измерения у объекта Тогда матрицы и задают бинарные отношения на множестве объектов . Поскольку бинарное отношение можно рассматривать как подмножество декартова квадрата , то любой матрице порядка из 0 и 1 соответствует бинарное отношение 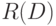, определяемое следующим образом: тогда и только тогда, когда .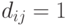

Бинарное отношение 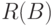- отношение эквивалентности, т.е. рефлексивное симметричное транзитивное отношение. Оно задает разбиение на классы эквивалентности. Два объекта и 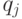входят в один класс эквивалентности тогда и только тогда, когда

Выше показано, как разбиения возникают в результате измерений в шкале наименований. Разбиения могут появляться и непосредственно. Так, при оценке качества промышленной продукции эксперты дают разбиение показателей качества на группы. Для изучения психологического состояния людей их просят разбить предъявленные рисунки на группы сходных между собой. Аналогичная методика применяется и в иных экспериментальных психологических исследованиях, необходимых для оптимизации управления персоналом.

Во многих эконометрических задачах разбиения получаются "на выходе" (например, в кластер - анализе) или же используются на промежуточных этапах анализа данных (например, сначала проводят классификацию с целью выделения однородных групп, а затем в каждой группе строят регрессионную зависимость).

Бинарное отношение 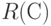задает разбиение на классы эквивалентности, между которыми введено отношение строгого порядка. Два объекта и 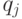входят в один класс тогда и только тогда, когда и 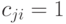, т.е. . Класс эквивалентности 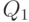предшествует классу эквивалентности 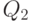тогда и только тогда, когда для любых 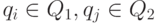имеем 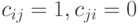, т.е. . Такое бинарное отношение в статистике часто называют ранжировкой со связями; связанными считаются объекты, входящие в один класс эквивалентности. В литературе встречаются и другие названия: линейный квазипорядок, упорядочение, квазисерия, ранжирование. Если каждый из классов эквивалентности состоит только из одного элемента, то имеем обычную ранжировку (другими словами, линейный порядок).

Как известно, ранжировки возникают в результате измерений в порядковой шкале. Так, при описанном выше опросе ответ выпускника школы - это ранжировка (со связями) профессий по привлекательности. Ранжировки часто возникают и непосредственно, без промежуточного этапа - приписывания объектам квазичисловых оценок - баллов. Многочисленные примеры тому даны М. Кендэлом [6]. При оценке качества промышленной продукции нормативные методические документы предусматривают использование ранжировок.

Для прикладных областей, кроме ранжировок и разбиений, представляют интерес толерантности, т.е. рефлексивные симметричные отношения. Толерантность - математическая модель для выражения представлений о сходстве (похожести, близости). Разбиения - частный вид толерантностей. Толерантность, обладающая свойством транзитивности - это разбиение. Однако в общем случае толерантность не обязана быть транзитивной. Толерантности появляются во многих постановках теории экспертных оценок, например, как результат парных сравнений (см. ниже).

Напомним, что любое бинарное отношение на конечном множестве может быть описано матрицей из 0 и 1.

Дихотомические (бинарные) данные. Это данные, которые могут принимать одно из двух значений (0 или 1), т.е. результаты измерений значений альтернативного признака. Как уже было показано, измерения в шкале наименований и порядковой шкале приводят к бинарным отношениям, а те могут быть выражены как результаты измерений по нескольким альтернативным признакам, соответствующим элементам матриц, описывающих отношения. Дихотомические данные возникают в прикладных исследованиях и многими иными путями.

В настоящее время в большинстве стандартов на конкретную продукцию предусмотрен контроль по альтернативному признаку. Это означает, что единица продукции относится к одной из двух категорий - "годных" или "дефектных", т.е. соответствующих или не соответствующих требованиям стандарта. Отечественными специалистами проведены обширные теоретические исследования проблем статистического приемочного контроля по альтернативному признаку. Основополагающими в этой области являются работы академика А.Н.Колмогорова. Подход советской вероятностно-статистической школы к проблемам контроля качества продукции отражен в монографиях [7], [8] (см. также "Эконометрические методы управления качеством и сертификации продукции" ).

Дихотомические данные - давний объект математической статистики. Особенно большое применение они имеют в экономических и социологических исследованиях, в которых большинство переменных, интересующих специалистов, измеряется по качественным шкалам. При этом дихотомические данные зачастую являются более адекватными, чем результаты измерений по методикам, использующим большее число градаций. В частности, психологические тесты типа MMPI используют только дихотомические данные. На них опираются и популярные в технико-экономическом анализе методы парных сравнений [9].

Элементарным актом в методе парных сравнений является предъявление эксперту для сравнения двух объектов (сравнение может проводиться также прибором). В одних постановках эксперт должен выбрать из двух объектов лучший по качеству, в других - ответить, похожи объекты или нет. В обоих случаях ответ эксперта можно выразить одной из двух цифр (меток)- 0 или 1. В первой постановке: 0, если лучшим объявлен первый объект; 1 - если второй. Во второй постановке: 0, если объекты похожи, схожи, близки; 1 - в противном случае.

Подводя итоги изложенному, можно сказать, что рассмотренные выше данные представимы в виде векторов из 0 и 1 (при этом матрицы, очевидно, могут быть записаны в виде векторов). Поскольку все результаты наблюдений имеют лишь несколько значащих цифр, то, используя двоичную систему счисления, любые виды анализируемых эконометрическими методами данных можно записать в виде векторов из 0 и 1. Представляется, что эта возможность имеет лишь академический интерес, но во всяком случае можно констатировать, что анализ дихотомических данных необходим во многих прикладных постановках.

Множества. Совокупность 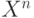векторов 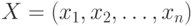из 0 и 1 размерности n находится во взаимно-однозначном соответствии с совокупностью всех подмножеств множества 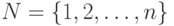. При этом вектору 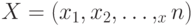соответствует подмножество 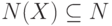, состоящее из тех и только из тех , для которых 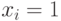. Это объясняет, почему изложение вероятностных и статистических результатов, относящихся к анализу данных, являющихся объектами нечисловой природы перечисленных выше видов, можно вести на языке конечных случайных множеств, как это было сделано в монографии [3].

Множества как исходные данные появляются и в иных постановках. Из геологических реалий исходил Ж. Матерон, из электротехнических - Н.Н. Ляшенко и др. Случайные множества применялись для описания процесса случайного распространения, например распространения информации, слухов, эпидемии или пожара, а также в математической экономике. В монографии [3] рассмотрены приложения случайных множеств в теории экспертных оценок и в теории управления запасами и ресурсами (логистике).

Отметим, что реальные объекты можно моделировать случайными множествами как из конечного числа элементов, так и из бесконечного, однако при расчетах на ЭВМ неизбежна дискретизация, т.е. переход к первой из названных возможностей.

Нечеткие множества. Пусть - некоторое множество. Подмножество множества характеризуется своей характеристической функцией

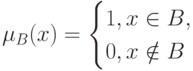( 1)

Что такое нечеткое множество? Обычно говорят, что нечеткое подмножество множества характеризуется своей функцией принадлежности Если функция принадлежности имеет вид (1) при некотором , то есть обычное (четкое) подмножество A.

Обычное подмножество можно было бы отождествить с его характеристической функцией. Этого математики не делают, поскольку для задания функции (в ныне принятом подходе) необходимо сначала задать множество. Нечеткое же подмножество с формальной точки зрения можно отождествить с его функцией принадлежности. Однако термин "нечеткое подмножество" предпочтительнее при построении математических моделей реальных явлений.

Начало современной теории нечеткости положено работой 1965 г. американского ученого азербайджанского происхождения Л.А.Заде. К настоящему времени по этой теории опубликованы тысячи книг и статей, издается несколько международных журналов, выполнено достаточно много как теоретических, так и прикладных работ.

Л.А. Заде рассматривал теорию нечетких множеств как аппарат анализа и моделирования гуманистических систем, т.е. систем, в которых участвует человек. Его подход опирается на предпосылку о том, что элементами мышления человека являются не числа, а элементы некоторых нечетких множеств или классов объектов, для которых переход от "принадлежности" к "непринадлежности" не скачкообразен, а непрерывен. В настоящее время методы теории нечеткости используются почти во всех прикладных областях, в том числе при управлении предприятием, качеством продукции и технологическими процессами.

Л.А. Заде использовал термин "fuzzy set" (нечеткое множество). На русский язык термин "fuzzy" переводили как нечеткий, размытый, расплывчатый, и даже как пушистый и туманный.

Аппарат теории нечеткости громоздок. В качестве примера дадим определения теоретико-множественных операций над нечеткими множествами. Пусть и - два нечетких подмножества с функциями принадлежности и 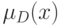соответственно. Пересечением 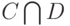, произведением 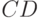, объединением 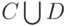, отрицанием 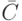, суммой 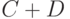называются нечеткие подмножества с функциями принадлежности

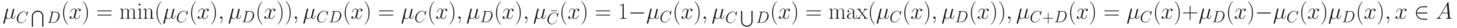
соответственно.

Теория нечетких множеств в определенном смысле сводится к теории вероятностей, а именно, к теории случайных множеств. Соответствующий цикл теорем приведен в книгах [3], [10]. Однако при решении прикладных задач вероятностно-статистические методы и методы теории нечеткости обычно рассматриваются как различные.

Объекты нечисловой природы как статистические данные. В эконометрике и прикладной математической статистике наиболее распространенный объект изучения - выборка , т.е. совокупность результатов наблюдений. В различных областях статистики результат наблюдения - это или число, или конечномерный вектор, или функция... Соответственно проводится деление прикладной математической статистики: одномерная статистика, многомерный статистический анализ, статистика временных рядов и случайных процессов... В статистике нечисловых данных в качестве результатов наблюдений рассматриваются объекты нечисловой природы, в частности, перечисленных выше видов - измерения в шкалах, отличных от абсолютной, бинарные отношения, вектора из 0 и 1, множества, нечеткие множества. Выборка может состоять из ранжировок или толерантностей, или множеств, или нечетких множеств и т.д.

Отметим необходимость развития методов статистической обработка "разнотипных данных", обусловленную большой ролью в прикладных исследованиях "признаков смешанной природы". Речь идет о том, что результат наблюдения состояния объекта зачастую представляет собой вектор, у которого часть координат измерена по шкале наименований, часть - по порядковой шкале, часть - по шкале интервалов и т.д. Статистические методы ориентированы обычно либо на абсолютную шкалу, либо на шкалу наименований (анализ таблиц сопряженности), а потому зачастую непригодны для обработки разнотипных данных. Есть и более сложные модели разнотипных данных, например, когда некоторые координаты вектора наблюдений описываются нечеткими множествами.

Для обозначения подобных неклассических результатов наблюдений в 1979 г. в монографии [3] предложен собирательный термин - объекты нечисловой природы. Термин "нечисловой" означает, что структура пространства, в котором лежат результаты наблюдений, не является структурой действительных чисел, векторов или функций, она вообще не является структурой линейного (векторного) пространства. При расчетах объекты числовой природы, разумеется, изображаются с помощью чисел, но эти числа нельзя складывать и умножать.

С целью "стандартизации математических орудий" целесообразно разрабатывать методы статистического анализа данных, пригодные одновременно для всех перечисленных выше видов результатов наблюдений. Кроме того, в процессе развития прикладных исследований выявляется необходимость использования новых видов объектов нечисловой природы, отличных от рассмотренных выше, например, в связи с развитием статистических методов обработки текстовой информации. Поэтому целесообразно ввести еще один вид объектов нечисловой природы - объекты произвольной природы, т.е. элементы множества, на которые не наложено никаких условий (кроме "условий регулярности", необходимых для справедливости доказываемых теорем). Другими словами, в этом случае предполагается, что результаты наблюдений (элементы выборки) лежат в произвольном пространстве X. Для получения теорем необходимо потребовать, чтобы X удовлетворяло некоторым условиям, например, было так называемым топологическим пространством. Как известно, ряд результатов классической математической статистики получен именно в такой постановке. Так, при изучении оценок максимального правдоподобия элементы выборки могут лежать в пространстве произвольной природы. Это не влияет на рассуждения, поскольку в них рассматривается лишь зависимость плотности вероятности от параметра. Методы классификации, использующие лишь расстояние между классифицируемыми объектами, могут применяться к совокупностям объектов произвольной природы, лишь бы в пространстве, где они лежат, была задана метрика. Цель статистики нечисловых данных (в некоторых литературных источниках используется термин "статистика объектов нечисловой природы") состоит в том, чтобы систематически рассматривать методы статистической обработки данных как произвольной природы, так и относящихся к указанным выше конкретным видам объектов нечисловой природы, т.е. методы описания данных, оценивания и проверки гипотез. Взгляд с общей точки зрения позволяет получить новые результаты и в других областях эконометрики.

Использование объектов нечисловой природы при формировании математической модели реального явления. Использование объектов нечисловой природы часто порождено желанием обрабатывать более объективную, более освобожденную от погрешностей информацию. Как показали многочисленные опыты, человек более правильно (и с меньшими затруднениями) отвечает на вопросы качественного например, сравнительного, характера, чем количественного. Так, ему легче сказать, какая из двух гирь тяжелее, чем указать их примерный вес в граммах. Другими словами, использование объектов нечисловой природы - средство повысить устойчивость эконометрических и экономико-математических моделей реальных явлений. Сначала конкретные области статистики объектов нечисловой природы (а именно, прикладная теория измерений, нечеткие и случайные множества) были рассмотрены в монографии [3] как частные постановки проблемы устойчивости математических моделей социально-экономических явлений и процессов к допустимым отклонениям исходных данных и предпосылок модели, а затем была понята необходимость проведения работ по развитию статистики объектов нечисловой природы как самостоятельного научного направления.

Начнем со шкал измерения. Науку о единстве мер и точности измерений называют метрологией. Таким образом, репрезентативная теория измерений - часть метрологии. Методы обработки данных должны быть адекватны относительно допустимых преобразований шкал измерения в смысле репрезентативной теории измерений. Однако установление типа шкалы, т.е. задание группы преобразований - дело специалиста соответствующей прикладной области. Так, оценки привлекательности профессий мы считали измеренными в порядковой шкале. Однако отдельные социологи не соглашались с этим, считая, что выпускники школ пользуются шкалой с более узкой группой допустимых преобразований, например, интервальной шкалой. Очевидно, эта проблема относится не к математике, а к наукам о человеке. Для ее решения может быть поставлен достаточно трудоемкий эксперимент. Пока же он не поставлен, целесообразно принимать порядковую шкалу, так как это гарантирует от возможных ошибок.

Порядковые шкалы широко распространены не только в социально-экономических исследованиях. Они применяются в медицине - шкала стадий гипертонической болезни по Мясникову, шкала степеней сердечной недостаточности по Стражеско-Василенко-Лангу, шкала степени выраженности коронарной недостаточности по Фогельсону; в минералогии - шкала Мооса (тальк - 1, гипс - 2, кальций - 3, флюорит - 4, апатит - 5, ортоклаз - 6, кварц - 7, топаз - 8, корунд - 9, алмаз - 10), по которому минералы классифицируются согласно критерию твердости; в географии - бофортова шкала ветров ("штиль", "слабый ветер", "умеренный ветер" и др.) и т.д. Напомним, что по шкале интервалов измеряют величину потенциальной энергии или координату точки на прямой, на которой не отмечены ни начало, ни единица измерения; по шкале отношений - большинство физических единиц: массу тела, длину, заряд, а также цены в экономике. Время измеряется по шкале разностей, если год принимаем естественной единицей измерения, и по шкале интервалов в общем случае. В процессе развития соответствующей области знания тип шкалы может меняться. Так, сначала температура измерялась по порядковой шкале (холоднее - теплее), затем - по интервальной (шкалы Цельсия, Фаренгейта, Реомюра) и, наконец, после открытия абсолютного нуля температур - по шкале отношений (шкала Кельвина). Следует отметить, что среди специалистов иногда имеются разногласия по поводу того, по каким шкалам следует считать измеренными те или иные реальные величины.

Отметим, что термин "репрезентативная" использовался, чтобы отличить рассматриваемый подход к теории измерений от классической метрологии, а также от работ А.Н.Колмогорова и А. Лебега, связанных с измерением геометрических величин, от "алгоритмической теории измерения" и др.

Необходимость использования в математических моделях реальных явлений таких объектов нечисловой природы, как бинарные отношения, множества, нечеткие множества, кратко была показана выше. Здесь же обратим внимание, что используемые в классической статистике результаты наблюдений также "не совсем числа". А именно, любая величина X измеряется всегда с некоторой погрешностью и результатом наблюдения является

Как уже отмечалось, погрешностями измерений занимается метрология. Отметим справедливость следующих фактов:

• для большинства реальных измерений невозможно полностью исключить систематическую ошибку, т.е.
• распределение 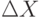в подавляющем большинстве случаев не является нормальным (см. "Статистический анализ числовых величин (непараметрическая статистика)" );
• измеряемую величину и погрешность ее измерения 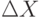обычно нельзя считать независимыми случайными величинами;
• распределение погрешностей оценивается по результатам специальных наблюдений, следовательно, полностью известным считать его нельзя; зачастую исследователь располагает лишь границами для систематической погрешности и оценками таких характеристик для случайной погрешности, как дисперсия или размах.

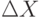Приведенные факты показывают ограниченность области применимости распространенной модели погрешностей, в которой и рассматриваются как независимые случайные величины, причем 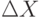имеет нормальное распределение с нулевым математическим ожиданием.

Строго говоря, результаты наблюдения всегда имеют дискретное распределение, поскольку описываются числами с небольшими (1 - 5) числом значащих цифр. Возникает дилемма: либо признать, что непрерывные распределения - фикция, и прекратить ими пользоваться, либо считать, что непрерывные распределения имеют "реальные" величины , которые мы наблюдаем с принципиально неустранимой погрешностью 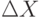. Первый выход в настоящее время нецелесообразен, так как потребует отказаться от большей части разработанного математического аппарата. Из второго следует необходимость изучения влияния неустранимых погрешностей на статистические выводы.

Погрешности 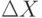можно учитывать либо с помощью вероятностной модели ( 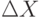- случайная величина, имеющая функцию распределения, вообще говоря, зависящую от ), либо с помощью нечетких множеств. Во втором случае приходим к теории нечетких чисел и к ее частному случаю - статистике интервальных данных (см. "Статистика интервальных данных" ).

Другой источник появления погрешности 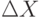связан с принятой в конструкторской и технологической документации системой допусков на контролируемые параметры изделий и деталей, с использованием шаблонов при проверке контроля качества продукции. В этих случаях характеристики 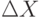определяются не свойствами средств измерения, а применяемой технологией проектирования и производства. В терминах математической статистики сказанному соответствует группировка данных, при которой мы знаем, какому из заданных интервалов принадлежит наблюдение, но не знаем точного значения результата наблюдения. Применение группировки может дать экономический эффект, поскольку зачастую легче (в среднем) установить, к какому интервалу относится результат наблюдения, чем точно измерить его.

Объекты нечисловой природы как результат статистической обработки данных. Объекты нечисловой природы появляются не только на "входе" статистической процедуры, но и в процессе обработки данных, и на "выходе" в качестве итога статистического анализа.

Рассмотрим простейшую прикладную постановку задачи регрессии (см. также "Многомерный статистический анализ" ). Исходные данные имеют вид 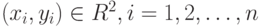. Цель состоит в том, чтобы с достаточной точностью описать y как полином от x, т.е. модель имеет вид

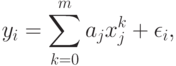( 2)

где - неизвестная степень полинома; 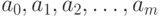- неизвестные коэффициенты многочлена; 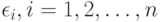, - погрешности, которые для простоты примем независимыми и имеющими одно и то же нормальное распределение. (Здесь наглядно проявляется одна из причин живучести модель на основе нормального распределения. Такие модели, хотя и неадекватны реальной ситуации, с математической точки зрения позволяет проникнуть глубже в суть изучаемого явления. Поэтому они пригодны для первоначального анализа ситуации, как и в рассматриваемом случае. Дальнейшие научные исследования должны быть направлены на снятие нереалистического предположения нормальности и перехода к непараметрическим моделям погрешности.) Распространенная процедура такова: сначала пытаются применить модель (2) для линейной функции 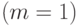, при неудаче (неадекватности модели) переходят к многочлену второго порядка 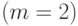, если снова неудача, то берут модель (2) с и т.д. (адекватность модели проверяют по -критерию Фишера).

Обсудим свойства этой процедуры в терминах математической статистики. Если степень полинома задана 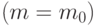, то его коэффициенты оценивают методом наименьших квадратов, свойства этих оценок хорошо известны (см., например, "Многомерный статистический анализ" или монографию [10, гл.26]). Однако в описанной выше реальной постановке m тоже является неизвестным параметром и подлежит оценке. Таким образом, требуется оценить объект 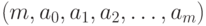, множество значений которого можно описать как 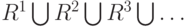Это - объект нечисловой природы, обычные методы оценивания для него неприменимы, так как m - дискретный параметр. В рассматриваемой постановке разработанные к настоящему времени методы оценивания степени полинома носят в основном эвристический характер (см., например, гл. 12 монографии [11]). Свойства описанной выше распространенной процедуры рассмотрены в "Многомерный статистический анализ" ; где показано, что при этом оценивается несостоятельно, и найдено предельное распределение оценки этого параметра, оказавшееся геометрическим.

В более общем случае линейной регрессии данные имеют вид где 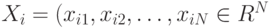- вектор предикторов (факторов, объясняющих переменных), а модель такова:

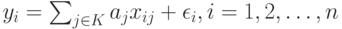( 3)

(здесь - некоторое подмножество множества 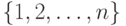; 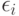- те же, что и в модели (2); 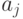- неизвестные коэффициенты при предикторах с номерами из K). Модель (2) сводится к модели (3), если

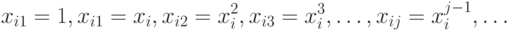
В модели (2) есть естественный порядок ввода предикторов в рассмотрение - в соответствии с возрастанием степени, а в модели (3) естественного порядка нет, поэтому здесь стоит произвольное подмножество множества предикторов. Есть только частичный порядок - чем мощность подмножества меньше, тем лучше. Модель (3) особенно актуальна в задачах управления качеством продукции и других технико-экономических исследованиях, в экономике, маркетинге и социологии, когда из большого числа факторов, предположительно влияющих на изучаемую переменную, надо отобрать по возможности наименьшее число значимых факторов и с их помощью сконструировать прогнозирующую формулу (3).

Задача оценивания модели (3) разбивается на две последовательные задачи: оценивание множества - подмножества множества всех предикторов, а затем - неизвестных параметров 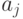. Методы решения второй задачи хорошо известны и подробно изучены. Гораздо хуже обстоит дело с оцениванием объекта нечисловой природы . Как уже отмечалось, существующие методы - в основном эвристические, они зачастую не являются даже состоятельными. Даже само понятие состоятельности в данном случае требует специального определения. Пусть - истинное подмножество предикторов, т.е. подмножество, для которого справедлива модель (3), а подмножество предикторов 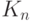- его оценка. Оценка 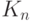называется состоятельной, если 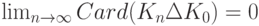где - символ симметрической разности множеств; означает число элементов в множестве , а предел понимается в смысле сходимости по вероятности.

Задача оценивания в моделях регрессии, таким образом, разбивается на две - оценивание структуры модели и оценивание параметров при заданной структуре. В модели (2) структура описывается неотрицательным целым числом , в модели (3) - множеством K. Структура - объект нечисловой природы. Задача ее оценивания сложна, в то время как задача оценивания численных параметров при заданной структуре хорошо изучена, разработаны эффективные (в смысле математической статистики) методы.

Такова же ситуация и в других методах многомерного статистического анализа - в факторном анализе (включая метод главных компонент) и в многомерном шкалировании. Ряд иных примеров можно найти в списке оптимизационных постановок основных проблем прикладного многомерного статистического анализа, приведенном в монографии [12].

Перейдем к объектам нечисловой природы на "выходе" статистической процедуры. Примеры многочисленны. Разбиения - итог работы многих алгоритмов классификации, в частности, алгоритмов кластер-анализа. Ранжировки - результат упорядочения профессий по привлекательности или автоматизированной обработки мнений экспертов - членов комиссии по подведению итогов конкурса научных работ. (В последнем случае используются ранжировки со связями; так, в одну группу, наиболее многочисленную, попадают работы, не получившие наград.) Из всех объектов нечисловой природы, видимо, наиболее часты на "выходе" дихотомические данные - принять или не принять гипотезу, в частности, принять или забраковать партию продукции. Результатом статистической обработка данных может быть множество, например зона наибольшего поражения при аварии, или последовательность множеств, например, "среднемерное" описание распространения пожара (см. "Статистический анализ числовых величин (непараметрическая статистика)" в монографии [3]). Нечетким множеством Э. Борель [13] еще в начале ХХ в. предлагал описывать представление людей о числе зерен, образующем "кучу". С помощью нечетких множеств формализуются значения лингвистических переменных, выступающих как итоговая оценка качества систем автоматизированного проектирования, сельскохозяйственных машин, бытовых газовых плит, надежности программного обеспечения или систем управления. Можно констатировать, что все виды объектов нечисловой природы могут появляться " на выходе"статистического исследования.