|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Эконометрический анализ инфляции
Определение индекса инфляции
Средняя цена и разброс цен. В конкретном акте купли-продажи цена товара или услуги полностью определена. Однако в современных условиях, когда в большинстве случаев продавец, а иногда и покупатель, могут влиять на цену товара или услуги, эта цена зачастую меняется от одного акта купли-продажи к другому.
Можно выделить несколько вариантов.
- Конкретный продавец меняет цену в зависимости от конкретного покупателя. Пример: индивидуальный продавец на базаре.
- В конкретном магазине цена фиксирована, но от магазина к магазину она меняется. Примеры: большинство товаров (продаваемых в магазинах и киосках), цены которых указаны для сведения покупателей.
- Единые цены в регионе, например, на услуги почтовой связи.
Пусть в определенный день (момент времени)  осуществлено
осуществлено  актов купли-продажи определенного товара, причем в акте с номером
актов купли-продажи определенного товара, причем в акте с номером  , где
, где 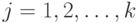 , куплено количество товара
, куплено количество товара 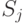 по цене
по цене 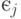 . Тогда экономическая ситуация описывается двумя векторами размерности
. Тогда экономическая ситуация описывается двумя векторами размерности  , а именно, вектором объемов продаж:
, а именно, вектором объемов продаж:
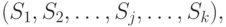
и вектором соответствующих цен:
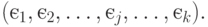
С целью проведения дальнейшего экономического анализа необходимо перейти к обобщенным характеристикам - к объему продаж-покупок:
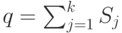
и средней цене за единицу товара:

Разумеется, при переходе от 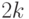 чисел к двум числам, т.е. при "сжатии информации", часть информации теряется. Подобный переход допустим, если все цены
чисел к двум числам, т.е. при "сжатии информации", часть информации теряется. Подобный переход допустим, если все цены 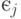 сравнительно мало отличаются от средней цены
сравнительно мало отличаются от средней цены  . В России 1993-1995 гг. с ежемесячным ростом цен не менее 5-10-20 % экономически значим именно общий рост цен. В ситуациях со стабильной средней ценой внимание экономистов привлекает разброс цен относительно средней
. В России 1993-1995 гг. с ежемесячным ростом цен не менее 5-10-20 % экономически значим именно общий рост цен. В ситуациях со стабильной средней ценой внимание экономистов привлекает разброс цен относительно средней  . Например, в современной Франции цены на определенный товар в фешенебельных центральных магазинах и в окраинных непрестижных супермаркетах могут отличаться в несколько раз. Это - одно из проявлений так называемой "ценовой диверсификации".
. Например, в современной Франции цены на определенный товар в фешенебельных центральных магазинах и в окраинных непрестижных супермаркетах могут отличаться в несколько раз. Это - одно из проявлений так называемой "ценовой диверсификации".
В Москве даже в период общей сильной инфляции также наблюдалось это явление, хотя и в гораздо меньших масштабах (табл.7.1).
| Наименование | Север - цена в руб. | Центр- цена в руб |
|---|---|---|
| Хлеб пшеничный | 370 | 390 |
| Огурцы | 1800 | 2000 |
| Яблоки | 2000 | 2500 |
| Молоко | 570 | 615 |
Измерения цен и объемов продаж относится к определенному моменту времени  , поэтому
, поэтому  и
и  являются функциями от
являются функциями от  , т.е.
, т.е. 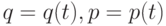 .
.
При этом время  принимает дискретные значения. Организации, ведущие экономический мониторинг, с 1991 г. измеряют цены с интервалом в неделю.
принимает дискретные значения. Организации, ведущие экономический мониторинг, с 1991 г. измеряют цены с интервалом в неделю.
Функция от дискретного (с постоянным шагом) временного параметра называется временным рядом. Анализом и прогнозированием временных рядов занимается специальный раздел эконометрики - статистика временных рядов (см. "Эконометрика временных рядов" ).
Потребительская корзина и доход. Рассмотрим конкретного покупателя, т.е. конкретного экономического субъекта: физическое лицо, домохозяйство или фирму. Он покупает не один товар, а много. Обозначим через  количество типов товаров или услуг (далее кратко - товаров), которые он хочет и может купить. Обозначим через
количество типов товаров или услуг (далее кратко - товаров), которые он хочет и может купить. Обозначим через

объемы покупок этих товаров по соответствующим ценам:
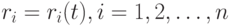
(имеется в виду цена за единицу измерения соответствующего товара - штуку или килограмм…).
Обратим внимание, что выше индекс  относится к различным актам купли-продажи, в которых участвуют различные продавцы и покупатели. В последних же рассмотрениях речь идет о покупках одного экономического субъекта, а потому используется иной индекс суммирования -
относится к различным актам купли-продажи, в которых участвуют различные продавцы и покупатели. В последних же рассмотрениях речь идет о покупках одного экономического субъекта, а потому используется иной индекс суммирования -  .
.
Расходы на покупки рассматриваемого экономического субъекта равны

Эту величину следует сопоставлять с доходом  рассматриваемого экономического субъекта. Если
рассматриваемого экономического субъекта. Если 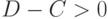 , то экономическое положение субъекта благоприятно, его доход больше расходов. Если же
, то экономическое положение субъекта благоприятно, его доход больше расходов. Если же 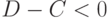 , то его положение неблагоприятно, доход меньше расходов. Это означает, что он расходует ранее накопленные средства, делает долги (в частности, берет кредиты) и т.д.
, то его положение неблагоприятно, доход меньше расходов. Это означает, что он расходует ранее накопленные средства, делает долги (в частности, берет кредиты) и т.д.
Из сказанного вытекает, что величина расходов 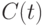 регулируется экономическим субъектом в соответствии с его доходом. Изменение (рост) цен
регулируется экономическим субъектом в соответствии с его доходом. Изменение (рост) цен 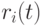 с течением времени
с течением времени  делает невозможным сохранение прежней структуры потребления
делает невозможным сохранение прежней структуры потребления 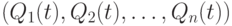 , если рост дохода отстает от роста цен. Структура потребления изменяется, сокращается потребление относительно дорогих товаров и услуг, в порядке компенсации увеличивается потребление относительно дешевых. Например, уменьшается потребление мяса и увеличивается - хлеба и картофеля. При быстром росте цен возможен и другой эффект - "бегство от рубля". В связи с обесцениванием сбережений экономические субъекты направляют доход на текущее потребление, ценой отказа от накопления средств на приобретение дорогостоящих товаров длительного пользования.
, если рост дохода отстает от роста цен. Структура потребления изменяется, сокращается потребление относительно дорогих товаров и услуг, в порядке компенсации увеличивается потребление относительно дешевых. Например, уменьшается потребление мяса и увеличивается - хлеба и картофеля. При быстром росте цен возможен и другой эффект - "бегство от рубля". В связи с обесцениванием сбережений экономические субъекты направляют доход на текущее потребление, ценой отказа от накопления средств на приобретение дорогостоящих товаров длительного пользования.
Проблемы усреднения темпов роста цен. Обсудим проблемы измерения роста цен на товары и услуги. Рассмотрим сначала конкретного экономического субъекта. Ясно, что цены на различные товары меняются по-разному. Для конкретного товара рост цены описывается величиной (индексом)
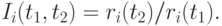
Эти индексы различны для различных товаров.
Одна из основных проблем в современной экономике - проблема агрегирования с целью сжатия информации (см., например, монографию [1]). Как свести к одной величине индексы цен для различных товаров и услуг?
Уровень цен выражается в виде индекса. Он является измерителем соотношения между совокупной ценой определенного набора товаров, называемого "рыночной корзиной" (или "потребительской корзиной"), для данного (текущего) момента времени, и совокупной ценой идентичной либо сходной группы товаров в базовый момент времени.
Первое, что приходит в голову - усреднить индексы для отдельных товаров и услуг. Но какое среднее взять? Среднее арифметическое? Среднее геометрическое? Среднее гармоническое? Среднее квадратическое? В экономике используется много различных видов средних (см., например, "Основы теории измерений" выше).
На первый взгляд, представляется естественным использовать взвешенное среднее арифметическое индексов роста цен на отдельные товары и услуги, а в качестве весов использовать относительные объемы потребления этих товаров и услуг. А именно, средним (или индексом) роста цен за интервал времени ![[t_1,t_2]](/sites/default/files/tex_cache/1de82f152537ed8c13fa0a0bbb3538a2.png) представляется естественным назвать величину
представляется естественным назвать величину
 |
( 1) |
где 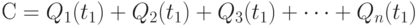
Обратите внимание на то, что индекс роста цен зависит от базовых значений цен и объемов потребления, определяемых в момент начала измерения 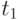 , и от текущих цен, измеренных в момент
, и от текущих цен, измеренных в момент 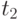 .
.
Очевидно, при реальных расчетах в качестве базового момента целесообразно брать тот, в котором соотношение различных товаров и услуг в потреблении является типичным для рассматриваемого экономического субъекта, т.е. базовый момент должен отражать стабильное потребление. Например, нельзя в качестве базового момента брать январь 1992 г., когда были отпущены цены на основные продукты и товары народного потребления. В январе 1992 г. структура потребления была сильно искажена, поскольку существенная часть населения, испытывая недостаток наличных денег, резко сократила закупки дорогостоящих товаров и услуг, в частности, используя накопленные запасы продуктов.
Пример 1. Пусть
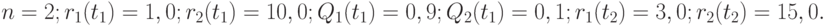
Тогда индекс роста цен согласно формуле (1) равен
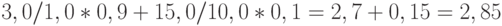
Введенный индекс роста цен меняется от одного экономического субъекта к другому. Он зависит как от структуры потребления конкретного субъекта, так и от цен, по которым тот покупает товары и услуги.
Например, резкий рост цен на сигареты отразится на индексе курящих, но не на индексе остальных физических лиц.
Цены могут зависеть от региона, а также от категории физических или юридических лиц. Так, в городе Иваново в июле 1993 г. сахарный песок отпускался по карточкам по цене 330 руб. за 1 кг. при рыночной цене 600 руб., а поллитровая бутылка водки - по цене 480 руб. при рыночной цене 800 руб.
Стоимостные весовые коэффициенты В чем очевидный экономический недостаток приведенной выше формулы (1) для индекса цен? В ней используется величина  - сумма объемов потребления
- сумма объемов потребления 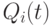 . При попытке ее расчета возникает необходимость складывать объемы потребления, выраженные в физических единицах измерения, например, килограммы картофеля складывать с буханками хлеба, бутылками молока, пачками сигарет и штуками холодильников. Тот читатель, кто этого не заметил, не справился с задачей, поставленной автором настоящей книги, на проверку соответствия экономико-математической модели здравому экономическому смыслу.
. При попытке ее расчета возникает необходимость складывать объемы потребления, выраженные в физических единицах измерения, например, килограммы картофеля складывать с буханками хлеба, бутылками молока, пачками сигарет и штуками холодильников. Тот читатель, кто этого не заметил, не справился с задачей, поставленной автором настоящей книги, на проверку соответствия экономико-математической модели здравому экономическому смыслу.
Ясно поэтому, что целесообразно измерять потребление не в физических единицах, а в стоимостных. Пусть

- доля потребления  -го продукта или услуги в общем потреблении
-го продукта или услуги в общем потреблении  (в стоимостном выражении).
(в стоимостном выражении).
Определение 1. Индексом инфляции называется

Пример 2. В условиях примера 1 объем потребления 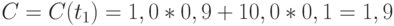 доля (в стоимостном выражении) первого продукта в потреблении равна
доля (в стоимостном выражении) первого продукта в потреблении равна  , доля второго (в стоимостном выражении) -
, доля второго (в стоимостном выражении) -  , индекс роста цен
, индекс роста цен
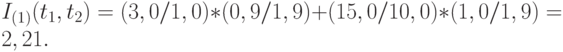
Результаты расчетов в примерах 1 и 2 различны. В этом нет ничего удивительного, поскольку используются разные весовые коэффициенты при вычислении взвешенного среднего. В этих примерах максимальный индекс роста цен для отдельных товаров есть 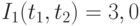 , минимальный
, минимальный 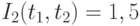 , а усредненные индексы
, а усредненные индексы 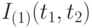 и
и 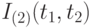 располагаются внутри интервала [1,5; 3,0]. Нетрудно показать, что любое число в этом интервале можно получить в качестве индекса роста цен, соответствующим образом подобрав объемы потребления.
располагаются внутри интервала [1,5; 3,0]. Нетрудно показать, что любое число в этом интервале можно получить в качестве индекса роста цен, соответствующим образом подобрав объемы потребления.
Сравнение стоимостей потребительских корзин. Другой подход к измерению роста цен основан на сравнении стоимостей потребительской корзины 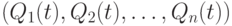 в старых
в старых  , и новых
, и новых 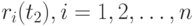 , ценах.
, ценах.
Определение 2. Индексом инфляции называется
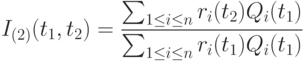
Пример 3. В условиях примера 1 стоимость потребительской корзины в старых ценах равна 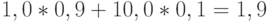 , в новых ценах ее стоимость равна
, в новых ценах ее стоимость равна 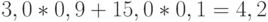 , и индекс роста цен (инфляции) равен
, и индекс роста цен (инфляции) равен
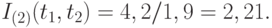
Эквивалентность двух подходов. В примерах 2 и 3 получился один и тот же результат. Случайно ли это? Оказывается, нет.
Теорема 1. Индексы инфляции, введенные согласно определениям 1 и 2, совпадают:

Доказательство дается следующей последовательностью преобразований:
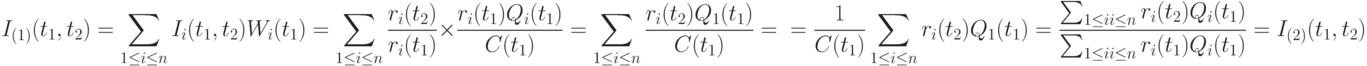
Обозначим
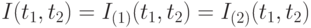
Эта величина называется индексом инфляции или индексом роста цен. При этом 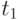 называется начальным, или базовым моментом времени, а
называется начальным, или базовым моментом времени, а 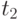 - текущим моментом времени.
- текущим моментом времени.
Теорема 1 допускает следующую полезную переформулировку (интерпретацию).
Теорема 2 (теорема сложения). Индекс инфляции 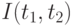 является средним арифметическим взвешенным индексов
является средним арифметическим взвешенным индексов 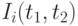 для отдельных товаров (услуг) или товарных групп:
для отдельных товаров (услуг) или товарных групп:
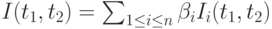
причем весовые коэффициенты 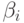 положительны и в сумме составляют 1. При этом
положительны и в сумме составляют 1. При этом 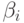 - это доля стоимости потребительской корзины, приходящаяся на соответствующий товар (услугу) в начальный (базовый) момент времени.
- это доля стоимости потребительской корзины, приходящаяся на соответствующий товар (услугу) в начальный (базовый) момент времени.
Для доказательства достаточно заметить, что