|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Принятие решений в стратегическом менеджменте
Проблема горизонта планирования в стратегическом менеджменте
Проблема горизонта планирования при управлении инвестициями. Во многих ситуациях продолжительность проекта не определена объективно (типичная ситуация для инноваций налоговой системы) либо горизонт планирования инвестора не охватывает всю продолжительность реализации проекта до этапа утилизации. Как уже отмечалось, в таких случаях важно изучить влияние горизонта планирования на принимаемые решения.
Рассмотрим условный пример. Предположим, гражданин Иванов получил в наследство свечной заводик в Самаре. Если его горизонт планирования - один месяц, то наибольший денежный доход он получит, немедленно продав предприятие. Если же он планирует на полгода - год, т.е. на интервал времени, больший, чем производственный цикл, то целесообразны инвестиции в оборотные средства предприятия. Сначала Иванов понесет затраты, закупив сырье, оплатив труд рабочих и осуществив иные необходимые выплаты, и только затем, продав продукцию, получит прибыль. Если Иванов планирует на достаточно продолжительный срок, скажем, на семь-десять лет, то для владельца экономически выгодны инвестиции в основные фонды предприятия. Он пойдет на крупные затраты, закупив лицензии и новое оборудование, с целью увеличения дохода в дальнейшие годы. При планировании на практически неограниченную перспективу - на двадцать-тридцать лет - имеет смысл вложить средства в создание и развитие собственного научно-исследовательского центра, и т.д.
Подчеркнем - реальные инвестиции (т.е. капиталовложения в основные фонды - в здания, оборудование, а также в конструкторские разработки и т.д.), которые окупятся в следующие годы, в текущем году ухудшат многие финансово-хозяйственные показатели работы предприятия, сократят его прибыль, уменьшат показатели рентабельности, в итоге акционеры получат - в данном году - меньше, чем получили бы при отсутствии инвестиций.
Из сказанного следует, что встречающееся иногда в литературе утверждение "фирма работает ради максимизации прибыли" не имеет точного смысла. За какой период максимизировать прибыль - за месяц, год, 10 или 30 лет? Как видно из примера, от горизонта планирования зависят принимаемые решения и соответствующие этим решениям экономические результаты. Например, при коротком периоде планирования целесообразны лишь инвестиции (капиталовложения) в оборотные фонды предприятия, и лишь при достаточно длительном периоде - в основные фонды.
Принимая во внимание зависимость оптимальных решений от горизонта планирования, ряд западных экономистов отказывается рассматривать фирмы как инструменты для извлечения прибыли. Они предпочитают рассматривать организации (предприятия) как структуры, аналогичные живым существам. Живые существа не стремятся к прибыли, у них другие цели. Прежде всего они стараются обеспечить свое нынешнее и будущее существование и развитие. Так и фирмы - они стремятся продолжить свое существование и расширить ареал обитания (в экономике - долю рынка). Речь идет об известной на Западе гипотезе Гэлбрейта - Баумола - Марриса ( Galbraith - Baumol - Marris ), в соответствии с которой в основе поведения корпораций лежит стремление к "максимальному росту", а не к "максимальной прибыли". Соответственно с этим стратегический менеджмент исходит из понятий "миссия фирмы", "стратегические цели" (например, стратегическая цель может иметь вид: "повысить долю рынка, контролируемую фирмой"), которые невозможно непосредственно выразить в денежных единицах.
Прежде чем обсуждать методы принятия решений в стратегическом менеджменте и непосредственно влияние горизонта планирования на решения менеджера, рассмотрим используемые при принятии решений оптимизационные модели.
Характеризация моделей с дисконтированием. Пусть для простоты изложения время принимает дискретные значения. Тогда динамику развития рассматриваемой экономической системы можно описать последовательностью 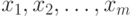 , где переменные
, где переменные  лежат в некотором пространстве Х, возможно, достаточно сложной природы. Надо отметить также, что положение экономической системы в следующий момент не может быть произвольным, оно связано с положением в предыдущий момент. Проще всего принять, что существует некоторое множество К такое, что
лежат в некотором пространстве Х, возможно, достаточно сложной природы. Надо отметить также, что положение экономической системы в следующий момент не может быть произвольным, оно связано с положением в предыдущий момент. Проще всего принять, что существует некоторое множество К такое, что  Результат экономической деятельности за j-й период описывается величиной
Результат экономической деятельности за j-й период описывается величиной 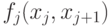 Зависимость не только от начального и конечного положения, но и от номера периода объясняется тем, что через номер периода осуществляется связь с общей (внешней) экономической ситуацией. Желая максимизировать суммарные результаты экономической деятельности, приходим к постановке стандартной задачи динамического программирования:
Зависимость не только от начального и конечного положения, но и от номера периода объясняется тем, что через номер периода осуществляется связь с общей (внешней) экономической ситуацией. Желая максимизировать суммарные результаты экономической деятельности, приходим к постановке стандартной задачи динамического программирования:
 |
( 1.1) |
Таким образом, необходимо выбрать план  удовлетворяющий приведенным ограничениям, на котором достигает максимума функционал
удовлетворяющий приведенным ограничениям, на котором достигает максимума функционал  . Естественно, предполагается, что множество возможных переходов К таково, что область определения функционала
. Естественно, предполагается, что множество возможных переходов К таково, что область определения функционала  не пуста. При обычных математических предположениях максимум достигается.
не пуста. При обычных математических предположениях максимум достигается.
Как известно, задача (1.1) часто возникает во многих прикладных экономических и эконометрических областях, в макроэкономике, в логистике (управлении запасами).
Широко предлагаются, исследуются и применяются модели, приводящие к следующему частному случаю задачи (1.1):
 |
( 1.2) |
Это - модели с дисконтированием (как известно,  - дисконт-фактор). Естественно попытаться выяснить, какими "внутренними" свойствами выделяются задачи типа (1.2) из всех задач типа (1.1). В частности, почему такой большой популярностью пользуется характеристика инвестиционного проекта NPV (Net Present Value - чистая текущая стоимость), относящаяся к характеристикам дисконтированного типа и подробно рассматриваемая ниже (в следующей главе).
- дисконт-фактор). Естественно попытаться выяснить, какими "внутренними" свойствами выделяются задачи типа (1.2) из всех задач типа (1.1). В частности, почему такой большой популярностью пользуется характеристика инвестиционного проекта NPV (Net Present Value - чистая текущая стоимость), относящаяся к характеристикам дисконтированного типа и подробно рассматриваемая ниже (в следующей главе).
Представляет интерес изучение и сравнение между собой планов возможного экономического поведения на k шагов  и
и  . (Естественно, предполагаем, что все пары соседних элементов входят в множество К.) Естественно сравнение проводить с помощью описывающих результаты экономической деятельности функций, участвующих в задачах (1.1) и (1.2). Именно, будем говорить, что план
. (Естественно, предполагаем, что все пары соседних элементов входят в множество К.) Естественно сравнение проводить с помощью описывающих результаты экономической деятельности функций, участвующих в задачах (1.1) и (1.2). Именно, будем говорить, что план 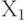 лучше плана
лучше плана 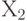 при реализации с момента i, если
при реализации с момента i, если
 |
( 1.3) |
Будем писать  , если выполнено неравенство (1.3), где R(i) - бинарное отношение на множестве планов, задающее упорядочение планов отношением "лучше при реализации с момента i".
, если выполнено неравенство (1.3), где R(i) - бинарное отношение на множестве планов, задающее упорядочение планов отношением "лучше при реализации с момента i".
Ясно, что упорядоченность планов на k шагов, определяемая с помощью бинарного отношения R(i), может зависеть от i, т.е. "хорошесть" плана зависит от того, с какого момента i он начинает осуществляться. С точки зрения реальной экономики это вполне понятно. Например, планы действий, вполне рациональные для периода стабильного развития, никуда не годятся в период гиперинфляции. И наоборот, приемлемые в период гиперинфляции операции не принесут эффекта в стабильной обстановке.
Однако, как легко видеть, в моделях с дисконтированием (1.2) все упорядочения R(i) совпадают, 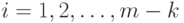 . Оказывается - это и есть основной результат настоящего подпункта - верно и обратное: если упорядочения совпадают, то мы имеем дело с задачей (1.2) - с задачей с дисконтированием, причем достаточно совпадения только при k = 1,2. Сформулируем более подробно предположения об устойчивости упорядочения планов.
. Оказывается - это и есть основной результат настоящего подпункта - верно и обратное: если упорядочения совпадают, то мы имеем дело с задачей (1.2) - с задачей с дисконтированием, причем достаточно совпадения только при k = 1,2. Сформулируем более подробно предположения об устойчивости упорядочения планов.
(I). Пусть  Верно одно из двух: либо
Верно одно из двух: либо

для всех  либо
либо

для всех 
(II). Пусть  Верно одно из двух: либо
Верно одно из двух: либо 
для всех  либо
либо

для всех 
Как впервые подробно показано в работе [3.4], при некоторых внутриматематических условиях регулярности из условий устойчивости упорядоченности планов (I) и (II) следует существование констант 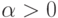 и
и  таких, что
таких, что

Поскольку прибавление константы не меняет точки, в которой функция достигает максимума, то последнее соотношение означает, что условия устойчивости упорядоченности планов (I) и (II) характеризуют (другими словами, однозначно выделяют) модели с дисконтированием среди всех моделей динамического программирования.
Математические условия, при которых доказывалась теорема о характеризации моделей с дисконтированием, постепенно ослаблялись на протяжении 1970-х годов , однако на экономическую сторону дела эти внутриматематические усовершенствования не влияли.
Асимптотически оптимальные планы. Рассмотрим модель (1.2) с 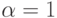 , т.е. модель без дисконтирования
, т.е. модель без дисконтирования

При естественных математических предположениях, на которых не будем останавливаться, при каждом m существует оптимальный план 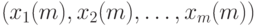 при котором достигает максимума оптимизируемая функция. Поскольку выбор горизонта планирования, как правило, нельзя рационально обосновать, хотелось бы построить план действий, близкий к оптимальному плану при различных горизонтах планирования. Это значит, что целью является построение бесконечной последовательности
при котором достигает максимума оптимизируемая функция. Поскольку выбор горизонта планирования, как правило, нельзя рационально обосновать, хотелось бы построить план действий, близкий к оптимальному плану при различных горизонтах планирования. Это значит, что целью является построение бесконечной последовательности 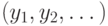 такой, что ее начальный отрезок длины m, т.е.
такой, что ее начальный отрезок длины m, т.е. 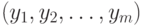 , дает примерно такое же значение оптимизируемого функционала, как и значение для оптимального плана
, дает примерно такое же значение оптимизируемого функционала, как и значение для оптимального плана 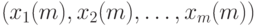 Бесконечную последовательность
Бесконечную последовательность 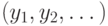 с указанным свойством назовем асимптотически оптимальным планом.
с указанным свойством назовем асимптотически оптимальным планом.
Выясним, можно ли использовать для построения асимптотически оптимального плана непосредственно оптимальный план. Зафиксируем k и рассмотрим последовательность , m = 1, 2, ... Нетрудно построить примеры, показывающие, что, во-первых, элементы в этой последовательности будут меняться; во-вторых, они могут не иметь пределов. Следовательно, оптимальные планы могут вести себя крайне нерегулярно, а потому в таких случаях их нельзя использовать для построения асимптотически оптимальных планов.
Тем не менее, можно доказать, что асимптотически оптимальные планы существуют, т.е. можно указать такие бесконечные последовательности 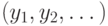 , что
, что

С помощью такого подхода решается проблема горизонта планирования - надо использовать асимптотически оптимальные планы, не зависящие от горизонта планирования.
Интересно, что оптимальная траектория движения состоит из трех участков - начального, конечного и основного, а основной участок - это движение по магистрали. Полная аналогия с движением автотранспорта: чтобы попасть куда-либо, нужно сначала выехать на магистраль (шоссе), подъехать по хорошей дороге возможно ближе к цели, потом преодолеть заключительный участок.
