|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Методы повышения экономической эффективности ПКС на основе моделирования и оптимизации внутрикорпоративных потоков
Величину кредиторской задолженности следует рассчитывать аналогично тому, как это сделано для активов, т. е. как результат притоков и оттоков. Следствием записи интегральных соотношений, аналогичных (5.1) и (5.2), будет необходимость описывать кредиторскую задолженность неположительными числами.
![K(t) = K(0) + \int\limits_{0}^{t}{[f_{opl}(t) - f_{pos}(t)]dt},](/sites/default/files/tex_cache/42337b0c059ede5bfbbf5694d39b5e5b.png) |
( 5.6) |
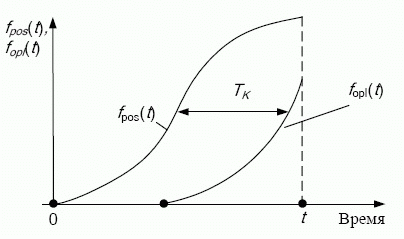
Определенные интегралы - это суммарные притоки и оттоки по входящему и исходящему потоку соответственно, за период от момента времени  до
до  . Притокоплата отстает во времени от оттокапоставок. Поэтому остаток - кредиторская задолженность - будет отрицательным, учитывая, что в начальный момент существования предприятия кредиторская задолженность
. Притокоплата отстает во времени от оттокапоставок. Поэтому остаток - кредиторская задолженность - будет отрицательным, учитывая, что в начальный момент существования предприятия кредиторская задолженность  была нулевая.
была нулевая.
Данное обстоятельство можно пояснить, изображая график оплаты, сдвинутый вправо по отношению к графику поставок (
рис. 5.4). Третье, отрицательное слагаемое в выражении (5.6), отток, численно равно площади под кривой поставок; второе, положительное слагаемое в (5.6), приток, изображается площадью под кривой оплаты. Кривая оплаты получена в результате сдвига вправо на период  . Поэтому площадь под ней всегда меньше. Следовательно, отрицательное слагаемое в (5.6) по абсолютной величине всегда больше положительного, что означает, учитывая
. Поэтому площадь под ней всегда меньше. Следовательно, отрицательное слагаемое в (5.6) по абсолютной величине всегда больше положительного, что означает, учитывая 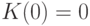 , отрицательность кредиторской задолженности.
, отрицательность кредиторской задолженности.
Более удобная форма записи (5.6) получается после дифференцирования по времени:
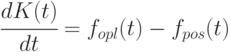 |
( 5.7) |
Рассмотренные зависимости между интенсивностями потоков, активами и источниками средств, существо которых состоит в балансе притоков и оттоков по отношению к некоторым накопителям, наглядно иллюстрируются в правой части рис. 5.3. Величины активов представлены в виде накопителей - "емкостей" с содержимым, изображаемым положительными значениями переменных величин. Величина кредиторской задолженности показана как изъятие из накопителя, отрицательное по отношению к нулевому уровню.
В начальный момент существования любого предприятия средства вносятся в уставный фонд, как правило, в денежной форме. Таким образом, сумма уставного фонда рассматриваемого простейшего предприятия равна сумме денежных средств 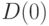 в момент
в момент  . Так как нет нераспределенной прибыли, присоединяемой к собственным средствам, то сумма последних всегда равна уставному фонду, следовательно, денежным средствам
. Так как нет нераспределенной прибыли, присоединяемой к собственным средствам, то сумма последних всегда равна уставному фонду, следовательно, денежным средствам 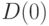 в момент
в момент  . Аналогично случаю кредиторской задолженности, в математической модели собственные средства изображаются накопителем с отрицательным содержимым:
. Аналогично случаю кредиторской задолженности, в математической модели собственные средства изображаются накопителем с отрицательным содержимым:
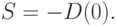 |
( 5.8) |
Это позволяет записать уравнение баланса активов и источников средств. Уравнение получается путем почленного сложения выражений (5.1), (5.2) и (5.6):
 |
( 5.9) |
Учитывая, что  и
и 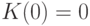 , т. е. в момент начала существования предприятия запаса товаров и задолженности нет; учитывая (5.8), получается уравнение баланса:
, т. е. в момент начала существования предприятия запаса товаров и задолженности нет; учитывая (5.8), получается уравнение баланса:
 |
( t) = - ) |
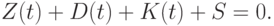 |
( 5.10) |
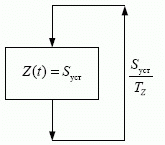
Выше обоснована взаимозависимость текущей интенсивности потока продаж и текущего запаса (см. рис. 5.1). Применительно к простейшему предприятию можно сказать, что продажи не могут быть больше того, что позволяет наличный запас товаров. С другой стороны, при данной интенсивности потока продаж запас товаров не может быть ниже некоторого уровня.
Простейшее предприятие здесь рассматривается в условиях, когда фактор ограниченности пропускной способности не проявляется, т. е. пропускная способность имеется "с запасом" и интенсивность продаж находится в пределах линейного участка графика ( рис. 5.1). Тогда взаимозависимость можно представить в виде неравенства
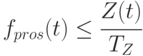 |
( 5.11) |
где 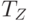 - норма оборачиваемости запаса товаров в ед. времени, показатель оборачиваемости.
- норма оборачиваемости запаса товаров в ед. времени, показатель оборачиваемости.
Это неравенство означает, что на рис. 5.1 точка, изображающая текущее состояние предприятия, не может находиться выше линии графика. Точка находится ниже линии графика, если при данном запасе продажи меньше того, что позволяет запас, т. е. предприятие искусственно уменьшает продажи по сравнению с рыночными, товар "придерживается". Можно также сказать, что изображающая точка находится правее линии графика, если при данных продажах имеется запас товаров, избыточный по отношению к необходимому для текущих рыночных продаж. Если же деятельность предприятия осуществляется без искусственного "придерживания" товара и без избыточного запаса, то изображающая точка находится на линии графика, а выражение (5.11) следует рассматривать только в виде строгого равенства.
Простейшее предприятие функционирует в изменяющейся рыночной среде, что представляется с помощью переменной величины 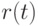 , зависящей от времени и обозначающей максимальное значение интенсивности потока продаж, достижимое предприятием исходя из текущего рыночного спроса:
, зависящей от времени и обозначающей максимальное значение интенсивности потока продаж, достижимое предприятием исходя из текущего рыночного спроса:
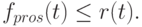 |
( 5.12) |
Математическая модель дополняется формальными ограничениями на неотрицательность переменных величин:
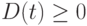 |
( 5.13) |
 |
( 5.14) |
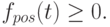 |
( 5.15) |
Выражение (5.13) означает, что отток денежных средств не должен приводить к их дефициту, выражения (5.14) и (5.15) фиксируют однонаправленность соответствующих потоков, что можно понимать как запрет возврата товаров покупателями и поставщикам.
Для удобства дальнейшего анализа выявленные количественные соотношения желательно расположить компактно в одном месте текста. Итак, рассматриваемая математическая модель функционирования предприятия записывается в виде следующей системы уравнений и неравенств:
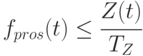 |
( 5.16) |
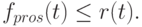 |
( 5.17) |
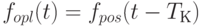 |
( 5.18) |
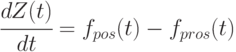 |
( 5.19) |
 |
( 5.20) |
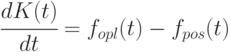 |
( 5.21) |
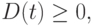 |
( 5.22) |
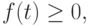 |
( 5.23) |
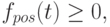 |
( 5.24) |
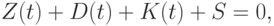 |
( 5.25) |
в которой параметрами являются  ,
,  и
и  .
.
Математическая модель однозначно определяет протекающие процессы при отсутствии "придерживания" товаров и избыточного запаса, т. е. когда соотношение (5.16) рассматривается только в случае равенства: имеется шесть переменных величин (три интенсивности потоков и три переменных содержимого накопителей) и шесть равенств (5.16, 5.18, 5.19, 5.20, 5.21 и 5.25). Неравенства (5.17, 5.22, 5.23 и 5.24) выступают в качестве ограничений, накладываемых на протекающие процессы.
Известно (см., например, [
7]), что период оборачиваемости запаса товаров, как правило, больше периода отсрочки оплаты поставок. Поэтому задача планирования рассматривается в условиях 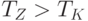 .
.
Задача планирования и исследование функционирования простейшей модели предприятия в условиях известных ограничений рыночных продаж.В самом общем виде задача планирования состоит в формировании плана функционирования при условии, что известны начальное состояние предприятия и максимальные интенсивности потока продаж в каждый момент периода планирования, обусловленные спросом, - прогноз спроса. Таким образом, изменение рыночной среды считается известным, поскольку изменения связываются с предсказуемым фактором сезонности. Так как деятельность простейшего предприятия рассматривается в краткосрочной перспективе, период планирования меньше или равен году, а наиболее общим критерием оптимальности планов следует считать рентабельность собственных средств. Такой критерий, как известно, - отношение годовой прибыли к величине собственных средств.
В простейшем предприятии из-за полного изъятия прибыли собственные средства постоянны, и поэтому, а также по причине принимаемого предположения о неизменности цен, рентабельность прямо пропорциональна годовому объему продаж, который и рассматривается здесь в качестве критерия оптимальности.
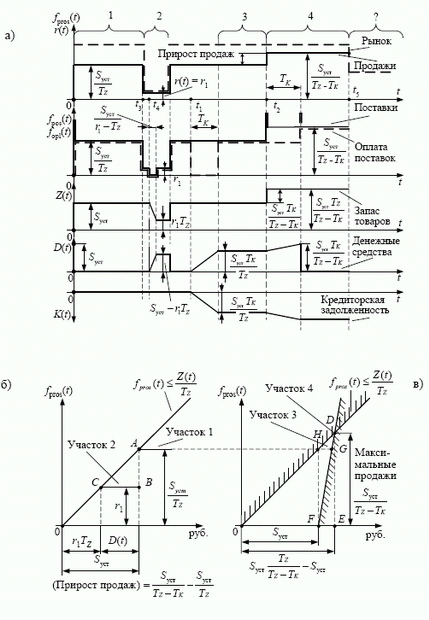
С целью уточнения постановки задачи выполняется исследование функционирования простейшего предприятия в условиях различных, но известных рыночных ограничений продаж ( рис. 5.5), что позволяет выяснить некоторые вопросы получения оптимальных решений.
а ) - процессы изменения переменных величин, б ) - анализ функционирования до получения товарного кредита, в ) - анализ функционирования в условиях товарного кредита поставщиков
Деятельность предприятия рассматривается с момента его образования  , последовательно на отрезках времени (участках) 1, 2, 3 и 4, обозначенных в верхней части
рис. 5.5. Для лучшего уяснения особенностей управления потоками при использовании товарного кредита предприятие рассматривается сначала в случае, когда поставщик не предоставляет отсрочку оплаты.
, последовательно на отрезках времени (участках) 1, 2, 3 и 4, обозначенных в верхней части
рис. 5.5. Для лучшего уяснения особенностей управления потоками при использовании товарного кредита предприятие рассматривается сначала в случае, когда поставщик не предоставляет отсрочку оплаты.
Рыночные ограничения максимальной интенсивности потока продаж  , изображенные в верхней части рисунка, изменяются, принимая значения двух уровней: повышенного, когда максимально допускаемые рынком продажи достаточно велики и заведомо превышают возможности предприятия (участки 1, 3 и 4), и пониженного (участок 2 и период времени после окончания участка 4). При повышенном рынке ограничения как бы не существуют, тогда как при пониженном рынке они существенны для деятельности предприятия.
, изображенные в верхней части рисунка, изменяются, принимая значения двух уровней: повышенного, когда максимально допускаемые рынком продажи достаточно велики и заведомо превышают возможности предприятия (участки 1, 3 и 4), и пониженного (участок 2 и период времени после окончания участка 4). При повышенном рынке ограничения как бы не существуют, тогда как при пониженном рынке они существенны для деятельности предприятия.
При повышенном рынке можно не учитывать ограничение, записанное в математической модели в виде неравенства (5.17) и отражающее ограниченность продаж спросом. Поэтому на участке повышенного спроса 1 продажи в текущий момент ограничиваются величиной запаса товаров в соответствии с неравенством (5.16). Желая получить максимум продаж, необходимо иметь возможно больший запас товаров. Поэтому все средства предприятия необходимо держать в виде товаров. Именно такой режим функционирования показан на графиках рис. 5.5 для участка 1.
В начале участка показан процесс перехода предприятия в этот режим. В момент  , когда образовывалось предприятие, в уставный фонд внесена некоторая сумма средств
, когда образовывалось предприятие, в уставный фонд внесена некоторая сумма средств  в денежной форме, сформировавшая уставный фонд. На графике денежных средств это состояние средств показано точкой
в денежной форме, сформировавшая уставный фонд. На графике денежных средств это состояние средств показано точкой  . В соответствии с обоснованным выше способом математического моделирования источников средств с помощью неположительных чисел, в начальный момент деятельности
. В соответствии с обоснованным выше способом математического моделирования источников средств с помощью неположительных чисел, в начальный момент деятельности  собственные средства
собственные средства 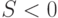 , их абсолютная величина равна сумме внесенных денежных средств:
, их абсолютная величина равна сумме внесенных денежных средств:

 |
( 5.26) |
(Можно считать, что денежные средства вносились в уставный фонд по самостоятельному потоку, входящему в блок  , см.
рис. 5.3, и исходящему из блока
, см.
рис. 5.3, и исходящему из блока  , в результате чего в последнем зафиксировано изъятие средств, представляемое отрицательным числом. С целью упростить рисунок на нем такой поток формирования уставного фонда не показан.)
, в результате чего в последнем зафиксировано изъятие средств, представляемое отрицательным числом. С целью упростить рисунок на нем такой поток формирования уставного фонда не показан.)
В начальный момент  уравнение баланса (5.25) записывается в виде:
уравнение баланса (5.25) записывается в виде:
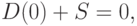 |
( 5.27) |
поскольку в этот момент запасы и кредиторская задолженность нулевые, и что соответствует выражению (5.26).
Очевидно, максимум продаж требует быстрейшей конвертации всех имеющихся денежных средств 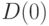 в запас товаров, что можно сделать, приобретая партию товаров на имеющуюся сумму. На графике денежных средств такое приобретение показано их скачкообразным уменьшением до нулевого уровня, на графике интенсивности потока продаж приобретение партии условно изображено в виде импульса, площадь которого подразумевается равной
в запас товаров, что можно сделать, приобретая партию товаров на имеющуюся сумму. На графике денежных средств такое приобретение показано их скачкообразным уменьшением до нулевого уровня, на графике интенсивности потока продаж приобретение партии условно изображено в виде импульса, площадь которого подразумевается равной 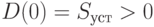 . Отметим, что приобретение партии считается мгновенным. Поэтому высота импульса на графике и соответствующая интенсивности потока бесконечно велики. Однако его площадь, соответствующую определенным интегралам в (5.1) и (5.2), следует считать равной величине партии.
. Отметим, что приобретение партии считается мгновенным. Поэтому высота импульса на графике и соответствующая интенсивности потока бесконечно велики. Однако его площадь, соответствующую определенным интегралам в (5.1) и (5.2), следует считать равной величине партии.
После поставки партии запас товаров становится равным  , продажи максимальны и равны максимально допустимым при данной величине запаса, их интенсивность находится по выражению (5.16), где положено
, продажи максимальны и равны максимально допустимым при данной величине запаса, их интенсивность находится по выражению (5.16), где положено 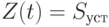 и взят случай равенства. Таким образом, на участке 1:
и взят случай равенства. Таким образом, на участке 1:
 |
( 5.28) |
Тот факт, что выражение (5.16), представляющее собой неравенство, использовано для расчета интенсивности сбыта в случае строгого равенства, означает, что возможности продаж используются "по максимуму", без какоголибо искусственного их ограничения и намеренного "придерживания" товара. На графике слева внизу рис. 5.5 точка A соответствует выражению (5.28).
Продажи приводят к расходу товаров. Поэтому их запас пополняется потоком поставок такой же интенсивности, что означает немедленное расходование денежных средств по получении выручки на оплату поставок и нулевой запас денежных средств. Поставки и их оплата синхронны, средства движутся через блок дебиторской задолженности "транзитом", и этот блок как бы не существует. Данный режим функционирования, поддерживаемый на участке 1, показан на рисунке, и очевидно, что он обеспечивает максимум продаж. В структурной схеме потоков для функционирования на участке 1 (рис. 5.6) три потока - продаж, поставок и их оплаты - представляют собой один поток.
На участке 2 в момент  рынок уменьшился до величины
рынок уменьшился до величины  , меньшей, чем продажи на участке 1:
, меньшей, чем продажи на участке 1:
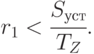 |
( 5.29) |
Из двух неравенств математической модели (5.16) и (5.17), ограничивающих продажи, актуальным становится (5.17), и максимальная интенсивность, достижимая на участке 2 из условия рыночного спроса, равна 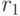 (см.
рис. 5.5, б, линия CB ). Для этой интенсивности продаж запас
(см.
рис. 5.5, б, линия CB ). Для этой интенсивности продаж запас  , сохранявшийся на предыдущем участке 1, становится избыточным, неравенство (5.16) выполняется "с запасом". В этих условиях существует две возможности:
, сохранявшийся на предыдущем участке 1, становится избыточным, неравенство (5.16) выполняется "с запасом". В этих условиях существует две возможности:
- всю выручку немедленно направлять на пополнение запаса, как это было на участке 1;
- учитывая избыточность запаса, временно прекратить поставки, уменьшив таким образом запас.
При реализации первой возможности запас остается на прежнем уровне  , так как имеется равенство притока и оттока. При этом интенсивность потока продаж и, следовательно, оплаты поставок следует поддерживать максимально возможной и равной
, так как имеется равенство притока и оттока. При этом интенсивность потока продаж и, следовательно, оплаты поставок следует поддерживать максимально возможной и равной 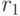 . Такое функционирование предприятия показано на начальном отрезке
. Такое функционирование предприятия показано на начальном отрезке ![[t_{3}, t_{4}]](/sites/default/files/tex_cache/c8a2c62e5a17c12cc182793b8f459a39.png) участка 2 и изображается точкой B на диаграмме слева внизу.
участка 2 и изображается точкой B на диаграмме слева внизу.
Вторая возможность реализуется после момента 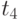 , когда поставки и синхронная с ними оплата были временно прекращены, в то время как продажи сохранялись максимально возможными и равными
, когда поставки и синхронная с ними оплата были временно прекращены, в то время как продажи сохранялись максимально возможными и равными 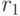 . В результате запас товаров уменьшался со скоростью продаж
. В результате запас товаров уменьшался со скоростью продаж 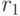 , а денежные средства наращивались от нулевой величины с этой же скоростью. Уменьшение запаса может продолжаться лишь до величины, соответствующей точке C (
рис. 5.5, внизу), и равной, исходя из (5.16)
, а денежные средства наращивались от нулевой величины с этой же скоростью. Уменьшение запаса может продолжаться лишь до величины, соответствующей точке C (
рис. 5.5, внизу), и равной, исходя из (5.16) 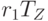 , так как в противном случае станет сказываться ограниченность продаж спросом и продажи нельзя будет поддерживать на максимальном
уровне
, так как в противном случае станет сказываться ограниченность продаж спросом и продажи нельзя будет поддерживать на максимальном
уровне 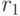 . Поэтому время, в течение которого поставки были прекращены (см.
рис. 5.5), рассчитывается как
. Поэтому время, в течение которого поставки были прекращены (см.
рис. 5.5), рассчитывается как
 |
( 5.30) |
где в числителе левой части записана величина избыточного запаса. За это время денежные средства возросли до уровня
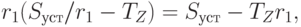 |
( 5.31) |
который находится как произведение скорости на время роста. Как видно, денежные средства возрастают на такую же сумму, что и уменьшение запаса, что можно показать также с помощью уравнения баланса (5.25), согласно которому, учитывая нулевую кредиторскую задолженность и постоянство собственных средств
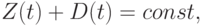 |
( 5.32) |
следовательно, равны и противоположны по знаку приращения  и
и  . На диаграмме периоду нулевых поставок соответствует движение от точки B к точке C, прирост денежных средств (5.31) может быть найден непосредственно по диаграмме.
. На диаграмме периоду нулевых поставок соответствует движение от точки B к точке C, прирост денежных средств (5.31) может быть найден непосредственно по диаграмме.
После возобновления поставок, чтобы поддерживать необходимый запас, их интенсивность должна равняться продажам 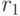 , что и показано на конечном отрезке участка 2. Обе возможности, с избыточным запасом и без такового, обеспечивают одинаковый объем продаж, и поэтому равноценны по отношению к рассматриваемой задаче.
, что и показано на конечном отрезке участка 2. Обе возможности, с избыточным запасом и без такового, обеспечивают одинаковый объем продаж, и поэтому равноценны по отношению к рассматриваемой задаче.
На графиках и диаграмме показаны крайние случаи без избыточного запаса товаров и без денежных средств. Из сказанного должно быть ясно, что возможны промежуточные случаи, с меньшим периодом нулевых поставок, что приведет к частичной конвертации избыточного запаса в денежные средства. При этом точка, изображающая состояние предприятия, будет находиться на отрезке CB внутри его.
В конце участка 2 рынок возвращается к прежнему повышенному уровню и поэтому до момента 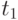 предприятие функционирует так же, как на участке 1.
предприятие функционирует так же, как на участке 1.
В момент 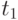 предприятие получает возможность пользования товарным кредитом. На отрезке времени от
предприятие получает возможность пользования товарным кредитом. На отрезке времени от 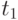 до
до 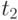 , то есть до конца участка 3, показано функционирование при условии, что сохраняются неизменными интенсивности потоков продаж и поставок, и, следовательно, величины запаса. В то же время предоставление отсрочки оплаты товаров на период
, то есть до конца участка 3, показано функционирование при условии, что сохраняются неизменными интенсивности потоков продаж и поставок, и, следовательно, величины запаса. В то же время предоставление отсрочки оплаты товаров на период 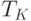 означает, что на отрезке
означает, что на отрезке ![[t_{1}, t_{1} + T_{K}]](/sites/default/files/tex_cache/5482a5e3e7bb03fdff2e081ce644c249.png) оплата поставок временно прекращается. Это приводит к росту денежных средств и возникновению кредиторской задолженности. В случае денежных средств постоянный приток равен продажам
оплата поставок временно прекращается. Это приводит к росту денежных средств и возникновению кредиторской задолженности. В случае денежных средств постоянный приток равен продажам 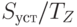 , отток в виде оплаты поставок отсутствует, следовательно, денежные средства линейно увеличиваются со скоростью притока и за время
, отток в виде оплаты поставок отсутствует, следовательно, денежные средства линейно увеличиваются со скоростью притока и за время 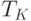 возрастают с нулевого уровня до
возрастают с нулевого уровня до 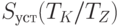 . Аналогично, абсолютная величина кредиторской задолженности за это время изменяется линейно и становится отрицательной (отток в отсутствие притока) и равной по абсолютной величине этому же значению.
. Аналогично, абсолютная величина кредиторской задолженности за это время изменяется линейно и становится отрицательной (отток в отсутствие притока) и равной по абсолютной величине этому же значению.
Таким образом, на участке 3 возникло новое состояние предприятия с увеличенными в результате товарного кредита источниками средств и соответствующим ростом активов на эту же сумму. Активы возросли за счет роста денежных средств при "старом" уровне запаса, продаж и поставок, поэтому существует возможность в соответствии с (5.16) увеличить продажи, конвертируя актив в виде денежных средств в запас товаров.
Так как желательно обеспечить максимум продаж, то такую конвертацию желательно сделать как можно быстрее. Очевидно, быстрее всего это можно сделать путем единовременной поставки партии товаров, что осуществляется в момент 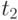 .
.