Совершенно секретные системы

Цель лекции: познакомиться с основными положениями теории информации, используемыми в криптографии и с принципами построения совершенно секретных систем.

Основные положения теории информации, используемые в криптографии, были сформулированы в середине ХХ века. Большой вклад в эти исследования внес американский ученый К. Шеннон. Для исследования принципов передачи информации по коммуникационным каналам Шеннон предложил вероятностный подход к оценке количества передаваемой информации. Кроме того, он показал, что в принципе возможны так называемые совершенно секретные криптографические системы, которые не могут быть "взломаны". Рассмотрим основные идеи теории Шеннона.

Основные подходы к измерению информации

Вопросы получения, обработки, передачи и защиты информации тесно связаны с проблемой ее количественного измерения. Выделяют несколько различных подходов к решению подобной проблемы, одним из которых является так называемый статистический (или алфавитный ) подход. Его суть заключается в том, что количественная оценка объема передаваемой информации осуществляется на основе анализа статистических характеристик источника информации. В этом способе учитывается способ представления информации с помощью какого-либо языка.

Очевидно, что информационная ценность некоторого сообщения связана с разнообразием вариантов генерируемых сообщений, или, другими словами, с разнообразием состояний источника информации. Ввиду этого можно считать, что объем информации, передаваемый отдельным сообщением, пропорционален общему числу N различных сообщений (или числу состояний источника информации). На практике, однако, в качестве меры информационной емкости принимается не само число N, а логарифм по основанию 2 от него:

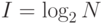
Данная формула позволяет получить результат в битах. Подобная мера получила название формально-логической логарифмической меры информации, или меры информации по Хартли.

Для однобуквенных сообщений N равно числу букв в алфавите информационного устройства. В частности, при числе букв равном двум количество информации

I = log 22 = 1 биту

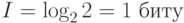
Например, рассмотрим источник, который генерирует сообщения, состоящие из одиночных букв русского языка, в алфавите которого 33 буквы. Определим, сколько информации несет отдельное сообщение, состоящее из одной буквы:

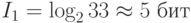
При таком подходе для определения количества информации в некотором сообщении надо количество символов в нем умножить на количество информации, содержащееся в одном символе, то есть на его информационный вес. Подсчитаем, какое количество информации несет сообщение, состоящее из четырех букв русского алфавита:

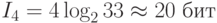
Таким образом, при алфавитном подходе объем информации в сообщении оценивается не по смыслу сообщения, а по статистическим характеристикам (количеству символов).

Мера Хартли не всегда является верной характеристикой сообщения, так как подразумевает равную вероятность любого из возможных сообщений. Так как ценность информации заключается в устранении имеющейся неопределенности, сообщения, имеющие высокую вероятность, менее ценны. Их можно в какой-то степени предвидеть заранее. И наоборот, маловероятные сообщения представляют большую ценность. Поэтому иногда используют другой способ количественной оценки информации, учитывающий вероятности генерации конкретных сообщений, – меру информации по Шеннону. Этот метод измерения информации называют также содержательным подходом.

Согласно этому методу состояние источника информации до получения сообщения потребителем характеризуется некоторой неопределенностью. При этом получение информации снимает эту неопределенность (полностью или частично):

I = H нач - Н кон

где H _нач – неопределенность, характеризующая источник сообщений до получения сообщения, а Н _кон – неопределенность после получения сообщения.

Неопределенность состояния источника информации оценивается по формуле

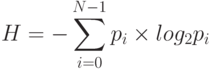
где p _i – вероятность i-го состояния источника. Знак "минус" перед суммой введен потому, что величины вероятностей являются правильными дробями и имеют отрицательные логарифмы, а оценку неопределенности нужно получить со знаком "плюс".

Рассмотрим пример. При вынимании шаров из урны, где находится один черный и один белый шар, неопределенность составляет

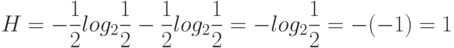
Неопределенность оказалась равной одному биту.

Рассмотрим другой пример. В урне находятся семь черных шаров и один белый. На этот раз неопределенность составит

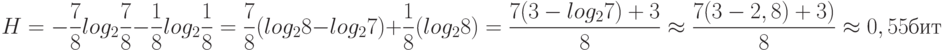
Мера неопределенности уменьшилась почти вдвое по сравнению с первым примером.

Неопределенность достигает максимального значения при равенстве вероятностей каждого из состояний друг другу и уменьшается с увеличением разброса этих вероятностей. Также следует заметить, что при равенстве вероятностей между собой , мера информации по Шеннону совпадает с мерой информации по Хартли.

Во многих случаях алфавитный подход к измерению информации оказывается предпочтительнее. Именно мера информации по Хартли используется, если мы говорим, что некоторый файл содержит 1,5 мегабайта информации или что на одной странице некоторой книги умещается 17 килобайт информации.

Основной единицей количества информации является бит. Однако для практического применения это слишком мелкая единица. Более удобной единицей является байт (byte), равный восьми битам. Прибавляя к слову "байт" децимальные приставки "кило", "мега" и так далее, можно получать более крупные единицы измерения. Нужно только помнить об условности таких обозначений, так как их связывает множитель, равный не 1000, а 1024 =2 ¹⁰.