Язык ПРОЛОГ: основные конструкции
Общая характеристика языка Пролог
Математическая логика дает нам ясный и точный язык для явного выражения знаний, гипотез и целей. Возможность машинного доказательства теорем, основанного на специальном выводе, названном принципом резолюций, впервые была получена Дж. Робинсон в 1965 году. Это привело к желанию построить язык программирования, который позволил бы реализовать одну из интеллектуальных сторон деятельности человека - проведение рассуждений в виде программ.
В начале 70-х годов прошлого века группой под руководством А. Колмероэ в Марселе на Фортране была написана программа для доказательства теорем, названная Прологом (от Programmation en Logique). Это привело в конце десятилетия к разработке языка Пролог и в дальнейшем развитию этого языка и в целом направления, которое получило название логического программирования.
Язык Пролог близок к модели Маркова: также основой является поиск подходящей подстановки - интерпретация переменных . Но подстановки ищутся в правилах языка (аналог рефал-предложений), и целью является именно поиск подстановки.
Программа на Прологе состоит из правил, которые представляют собой продукции с предикатами (относительно объектов) в левой и правой части. Тем самым программа Пролога выражает некоторые знания о внешнем мире (задаче или группе задач), необходимые для решения задач. Правила, не содержащие посылки в продукции, называются фактами , а вся система правил программы образует базу знаний .
Вопрос задачи, называемый запросом, - это также некоторый предикат, истинностью которого мы интересуемся. Если запрос не содержит переменных, то вычисление его значения дает ответ "Да" при его истинности либо ответ "Нет" при его ложности. Если же в предикате запроса есть переменные, то ищутся их значения ( интерпретация ), при которых этот предикат и все предикаты программы становятся истинными. В этом и состоят вычисления программы на Прологе.
Так как каждый предикат - это функция, то Пролог является языком функционального программирования.
Итак, в языке Пролог рассматриваются объекты и 3 вида утверждений относительно объектов: факты, правила и запросы. Единственной структурой данных является терм.
Объекты и термы Пролога
Объектами Пролога являются
- имена (начинаются со строчной буквы), строки символов (заключаются в апострофы) и числа - константные объекты или константы; например, автомобиль, дом, иван, 'a+b', 'X', 123;
- переменные - могут принимать значения других объектов, и мы их будем писать прописными латинскими буквами: например, X, A, W ;
- списки - их элементами являются любые объекты; списки мы заключаем в квадратные скобки, разделяя элементы запятыми; например, [] - пустой список (он является константой, мы его будем обозначать также nil и любой список завершать этим элементом, чтобы показать конец списка), [a, b, c, nil] - список, состоящий из трех констант a, b и c ; [X, [b, Y, 'X', nil], nil] - список, состоящий из двух элементов, первый из которых - переменная X, а второй - список из трех элементов: имени b, переменной Y и строки 'X'.
Завершающий список элемент nil можно при записи опускать, подразумевая его в необходимых случаях. Для конкатенации (соединения) списков и элементов в один список используется точка как бинарная операция соединения левой части (головы списка) и правой части (хвоста списка). В случае операции конкатенации квадратные скобки на нулевом уровне можно опускать. Например, a.X.Y.a при X=b, Y=c есть список [a, b, c, a], также при X=[b], Y=[c] есть тот же список, а при X=[b, [d, e]] и Y=[[c]] есть список [a, b, [d, e], [c], a].
Теперь индуктивно введем понятие терма. Термами являются объекты Пролога. Кроме того, термами являются составные термы. Составной терм образуется из имени функции и списка аргументов (термов Пролога) в круглых скобках. Синтаксически составной терм имеет вид
f(t1,..., tn),
где f - имя n -арного функтора, а  - аргументы.
- аргументы.
Примерами составных термов являются: холодный (вода), отец (иван, петр), list(d, list(b, nil)) и bintree(bintree(nil, 7, nil), L, 12).
В первом примере составным термом является высказывание с именем булевой функции 1 аргумента-константы, которое имеет логическое значение истина или ложь.
Во втором примере отношение "иван является отцом петра" задается как булева функция с 2 аргументами-константами.
В третьем примере бинарная функция с именем list и двумя аргументами имеет в качестве первого аргумента константный объект d , а в качестве второго аргумента - составной терм с именем той же функции и возвращает, по-видимому, список.
В четвертом примере функция с именем bintree и тремя аргументами возвращает в виде списков бинарное дерево с корнем 7, правым сыном 12 и левым сыном, который определяется переменной L.
Термы, в которые не входят переменные, назовем основными , а термы, содержащие переменные, - неосновными . Так, три первых примера выше являются основными термами, а четвертый пример - неосновным термом.
В логическом программировании основной структурой является предикатная функция, описываемая составным термом, которая имеет истинностное значение (истина или ложь), возможно зависящее от значений аргументов. Такой предикат называется атомарным, или атомом .
Факты
Факты - это простейшие утверждения относительно объектов программы, которые считаются истинными, т. е. имеют смысл аксиом программы. Каждый факт оформляется в виде атомарного предиката и стрелки влево, которая находится справа от него. Так, в следующем примере
мужчина (иван)<- мужчина (петр)<- отец (иван, петр)<- произведение (2, 2, 4)<-
задается, что объекты иван и петр являются мужчинами, что иван является отцом петра и что дважды два - четыре.
Почему ставится стрелка? Общий вид записи продукции "если A, то B ", где A и B - предикаты, выражается на Прологе следующим образом:
B <- A.
Факт не имеет посылки и читается "то B ", т. е. утверждение B рассматривается как истинный факт.
Множество фактов образуют простейшую программу Пролога. Но атомарный предикат факта может содержать переменные в качестве аргументов или неосновные термы. В этом случае по умолчанию считается, что добавлен квантор всеобщности 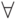 с переменными предиката. Такие факты называются универсальными: они истинны для любых значений переменных. Например,
с переменными предиката. Такие факты называются универсальными: они истинны для любых значений переменных. Например,
любит (X, яблоко)<-
означает, что любой объект программы "любит яблоко". Универсальные факты сокращают запись программы.
