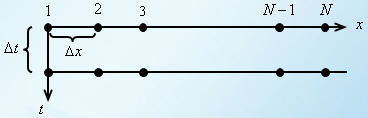
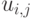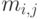НОУ ИНТУИТ | Программирование больших вычислительных задач на современном Фортране с использованием компиляторов Intel. Лекция 4: Математические библиотеки*

Опубликован: 18.12.2012 | Доступ: свободный | Студентов: 272 / 55 | Длительность: 03:25:00

Темы: Программирование, Суперкомпьютерные технологии

Специальности: Программист, Системный архитектор

Аннотация: Рассказывается о преимуществах использования библиотек поставляемых в среде Intel Parallel Studio. Рассматриваются основные разделы библиотеки Intel Math Kernel Library и её использование в Fortran-программах. (* www.intuit.ru Оптимизация приложений с использованием библиотеки Intel Math Kernel Library.)

Ключевые слова: векторные, операции, массив, входной

Презентацию к лекции Вы можете скачать здесь.

Обзор

Intel ® Math Kernel Library Основная математическая библиотека

Производительность (для больших задач)!

Параллельное выполнение!

Оптимизирована под процессоры Intel®!

IMSL International Mathematical and Statistical Library Международная математическая библиотека подпрограмм.

Компоненты IMSL

Процедуры линейной алгебры;
Решение систем линейных уравнений;
Преобразования Фурье и Лапласа;
Решение нелинейных уравнений;
Задачи оптимизации;
Сортировка и поиск данных;
Интерполяция и аппроксимация;
Интегрирование и дифференцирование;
Решение ОДУ;
Решение ДУЧП.

Компоненты MKL

BLAS	- базовые подпрограммы линейной алгебры;
Sparse BLAS	- BLAS для разреженных матриц;
LAPACK	- решатели задач линейной алгебры;
ScaLAPACK	- параллельное расширение LAPACK;
DFT	– дискретные преобразования Фурье;
Cluster DFT	– кластерные DFT;
Sparse Solvers	- решатели систем линейных уравнений с невырожденной разреженной матрицей;
VML (Vector Math Library)	– математические функции над векторами;
VSL (Vector Statistical Library)	– библиотека статистики;
PDEs (Partial Differential Equations)	– решатели уравнений в частных производных;
Optimization Solvers	– подпрограммы нелинейной оптимизации.

Настройка MS Visual Studio 2010

Расположение модулей (*.mod файлы)	C:\Program Files\Intel\ComposerXE-2011\mkl\include\ia32
Библиотеки	mkl_intel_c.lib mkl_intel_thread.lib libiomp5md.lib + mkl_blas95.lib mkl_lapack95.lib и др.
Расположение библиотек (*.lib файлы)	C:\Program Files\Intel\ComposerXE-2011\mkl\lib\ia32

Настройки проекта

Используем MKL Parallel

увеличить изображение

Библиотеки (в зависимости от процедур)

увеличить изображение

Документация и примеры

Документация пользователя (User guide)	C:\Program Files\Intel\ComposerXE-2011 \Documentation\en_US\mkl\mkl_userguide\ index.htm
Справочные страницы (Manual pages)	C:\Program Files\Intel\ComposerXE-2011\Documentation\en_US\mkl\mkl_manual\ index.htm
Примеры	C:\Program Files\Intel\ComposerXE- 2011\mkl\examples

Возможности на примере BLAS

Уровень 1 : Векторные операции

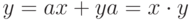
$y=ax+y\\a=x\cdot y$

Уровень 2 : Векторно-матричные операции

$y=aAx+by\\A=ax^T\cdot y+A$

Уровень 3 : Матричные операции

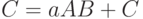
Хранение векторов

Элементы хранятся в одномерном массиве

n	- количество элементов;
incx	– шаг

incx > 0	- хранение по возрастанию;
incx < 0	- хранение по убыванию;
incx = 0	- все элементы равны значению x(1)

x = (1.0, 3.0, 5.0, 7.0, 9.0, 11.0, 13.0)

Если

incx = 2, n = 3 --> (1.0, 5.0, 9.0)

incx = -2,n = 4 --> (13.0, 9.0, 5.0, 1.0)

incx = 0, n = 5 --> (1.0, 1.0, 1.0, 1.0, 1.0)

Хранение матриц

Full Storage – элементы матрицы хранятся в двумерном массиве arr(i,j).

Для треугольных, симметричных или Эрмитовых матриц задание элементов массива определяется параметром uplo.

uplo = 'L'	- нижняя часть, с диагональю, i >= j
uplo = 'U'	- верхняя часть, с диагональю, i <= j

Остальные элементы необязательны.

character :: uplo = 'L'
real a(3,3)
  a(1,:) = (/1,0,0/)
  a(2,:) = (/2,5,0/)
  a(3,:) = (/3,0,9/)

Packed Storage – хранение симметричных, Эрмитовых или треугольных матриц : верхняя или нижняя треугольные части упаковываются по столбцам в одномерный массив.

uplo ='U', ---> arr(i+j*(j-1)/2), i <= j
uplo ='L', ---> arr(i+(2*n-j)*(j-1)/2), i >= j

Band Storage - ненулевые диагонали, матрицы размером (m x n), хранятся построчно в двумерном массиве arrB размером (kl+ku+1 x n), где

ku	– число диагоналей выше главной диагонали
kl	– число диагоналей ниже главной диагонали

При выполнении LU-факторизации над ленточными матрицами в массиве arrB следует добавить kl дополнительных строк.

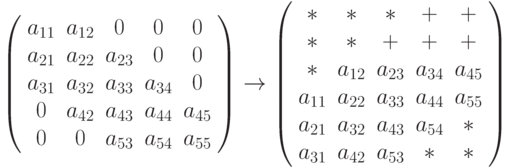
$\left(\begin{array}{cccсс}a_{11}&a_{12}&0&0&0\\ a_{21}&a_{22}&a_{23}&0&0\\ a_{31}&a_{32}&a_{33}&a_{34}&0\\ 0&a_{42}&a_{43}&a_{44}&a_{45}\\ 0&0&a_{53}&a_{54}&a_{55}\end{array}\right) \to \left(\begin{array}{cccсс}*&*&*&+&+\\ *&*&+&+&+\\ *&a_{12}&a_{23}&a_{34}&a_{45}\\ a_{11}&a_{22}&a_{33}&a_{44}&a_{55}\\ a_{21}&a_{32}&a_{43}&a_{54}&*\\ a_{31}&a_{42}&a_{53}&*&*\end{array}\right)$

*	- элементы не используемые в вычислениях
+	- используются для хранения результатов

После LU-факторизации входной массив arrB будет изменён следующим образом:

$u_{i,j}$	- элементы верхней треугольной матрицы;
$m_{i,j}$	- множители факторизации.

Пример. Подготовить матрицу для LU-факторизации.

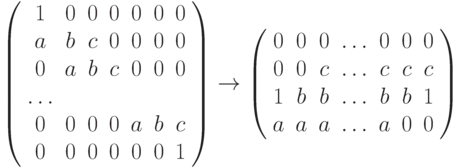
$\left(\begin{array}{ccccccc}1&0&0&0&0&0&0\\ a&b&c&0&0&0&0\\ 0&a&b&c&0&0&0\\ \ldots\\ 0&0&0&0&a&b&c\\ 0&0&0&0&0&0&1\end{array}\right) \to \left(\begin{array}{cccссcc}0&0&0&\ldots&0&0&0\\ 0&0&c&\ldots&c&c&c\\ 1&b&b&\ldots&b&b&1\\ a&a&a&\ldots&a&0&0\end{array}\right)$

ku = 1, kl = 1, m = 900, n=900.
arrB(2*kl+ku+1 x n) = (4 х 900).

integer, parameter :: m = 900
real :: arrB(4,m) = 0, a,b,c
arrB(2,3:m)   = c ! вторая, первую строку пропускаем
arrB(3,2:m-1) = b ! третья 
arrB(4,1:m-2) = a ! четвертая
arrB(3,1)=1; arrB(3,m)=1

Именование функций

Шаблон:

<character> <name> <mod> ( )
            <character>

s - real, single precision (вещественные данные одинарной точности)

c - complex, single precision (комплексные данные одинарной точности)

d - real, double precision (вещественные данные двойной точности)

z - complex, double precision (комплексные данные двойной точности)

Примеры

ddot <d> <dot>	- скалярное произведение двух векторов двойной точности
sgemv <s> <ge> <mv>	- матрично-векторное произведение, матрица обычная, одинарная точность
ztrmm <z> <tr> <mm>	- матрично-матричное произведение, треугольная матрица, комплексные числа двойной точности

Пример

Вычисление скалярного умножения

program prog
  use mkl95_blas
  integer, parameter :: n = 5    ! количество элементов
  real :: a(n) = (/1,2,3,4,5/),& ! векторы
          b(n) = (/2,4,6,8,9/)  
  real res
  res = dot(a,b) ! скалярное произведение
  write(*,*) "Scalar product = ", res
end

Результат вычислений

Scalar product =    105.0000
Для продолжения нажмите любую клавишу . . .

Пример

Решить одномерное уравнение теплопроводности методом конечных разностей.

Самостоятельно разобрать процедуры gbtrf, gbtrs.

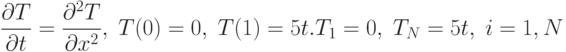
$\frac{\partial T}{\partial t}=\frac{\partial^2 T}{\partial x^2},\; T(0)=0,\; T(1)=5t.\\ \\ T_1=0,\; T_N=5t,\; i=1,N$

Пример

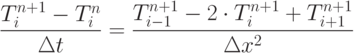
$\frac{T_i^{n+1}-T_i^n}{\Delta t}=\frac{T_{i-1}^{n+1}-2\cdot T_i^{n+1}+T_{i+1}^{n+1}}{\Delta x^2}$

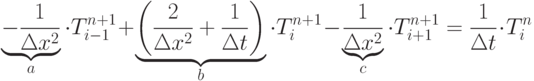
$\underbrace{-\frac 1{\Delta x^2}}_a \cdot T_{i-1}^{n+1} +\underbrace{\left(\frac 2{\Delta x^2}+\frac 1{\Delta t}\right)}_b \cdot T_i^{n+1} -\underbrace{\frac 1{\Delta x^2}}_c \cdot T_{i+1}^{n+1}=\frac 1{\Delta t}\cdot T_i^n$

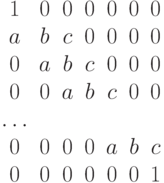
$\begin{array}{ccccccc}1&0&0&0&0&0&0\\ a&b&c&0&0&0&0\\ 0&a&b&c&0&0&0\\ 0&0&a&b&c&0&0\\ \ldots\\ 0&0&0&0&a&b&c\\ 0&0&0&0&0&0&1\end{array}\right)$

Вариант программы (1)

program teplo_1D
  use lapack95 
  use f95_precision
  
  integer, parameter :: N = 64
  integer k
 
  real DL(N-1), D(N), DU(N-1) ! DL - нижняя, D - основная, DU - верхняя
  real AB(4,N)
  real :: UN(N) = 0

  real :: dt = 0.01           ! --- шаг по времени
  real, parameter :: H = 1.0  ! --- длина области
  real :: dh = H/(N-1)        ! шаг по области   
  
  integer IPIV(N), INFO
  !======================================================================
  open(1,file = "res1.txt")
  open(3,file = "res2.txt")
  open(5,file = "res3.txt")
  
  !------ заполняем диагонали  
  !------ так как на границах Г.У. первого рода
  DL = -dt/dh**2;       DL(N-1) = 0          ! --- нижняя 
  D = 2*dt/dh**2+1;     D(1) = 1; D(N) = 1   ! --- основная
  DU = -dt/dh**2;       DU(1) = 0            ! --- верхняя

Вариант программы (2)

!----- формируем AB-матрицу
 AB(1,:) = 0      ! не заполняем, нужна для процедур
 AB(2,2:N) = DU
 AB(3,1:N) = D
 AB(4,1:N-1) = DL
 
 call gbtrf(AB, ipiv = IPIV)  ! ---- делаем факторизацию 
  do k = 1,500  
  UN(N) = 5*k*dt ! ----- правая часть
  call gbtrs(AB, UN, IPIV, info = INFO)  ! --- вызываем решатель
  if ((k == 100).OR.(k == 300).OR.(k == 500)) then
    do i = 1,N
      x = (i-1)*dh
      write(k/100,*) x, UN(i) 
     end do
     close(k/100) 
  end if 
 end do 
 close(1)
 close(3)
 close(5)
end

Дальше >>

Авторизоваться

Программирование больших вычислительных задач на современном Фортране с использованием компиляторов Intel

Математические библиотеки*

Обзор

Компоненты IMSL

Компоненты MKL

Настройка MS Visual Studio 2010

Настройки проекта

Документация и примеры

Возможности на примере BLAS

Хранение векторов

Хранение матриц

Именование функций

Пример

Пример

Пример

Вариант программы (1)

Вариант программы (2)

Вопросы и ответы