Технологии туннелирования
[+]
Московский государственный университет имени М.В.Ломоносова
Опубликован: 28.11.2014 | Доступ: свободный | Студентов: 0 / 0 | Длительность: 23:26:00
ISBN: 978-5-9556-0163-2
Темы: Сетевые технологии, Безопасность
Специальности: Администратор информационных систем, Специалист по безопасности, Администратор коммуникационных систем
Лекция 3:

Хэш-функции
A
|
версия для печати
< Лекция 2 || Лекция 3: 123456 || Лекция 4 >

Требования к криптографическим хэш-функциям

Хэш-функцией называется односторонняя функция, предназначенная для получения дайджеста или "отпечатков пальцев" файла, сообщения или некоторого блока данных.

Хэш-код создается функцией Н:

h = H (M)

гдеМ является сообщением произвольной длины и h является хэш-кодом фиксированной длины.

Рассмотрим требования, которым должна соответствовать хэш-функция для того, чтобы она могла использоваться в качестве аутентификатора сообщения.

Чтобы хэш-функция Н могла использоваться в качестве аутентификатора сообщения, она должна обладать следующими свойствами:

  1. Хэш-функция Н должна применяться к блоку данных любой длины.
  2. Хэш-функция Н должна создавать выход фиксированной длины.
  3. Н(М) относительно легко (за полиномиальное время) вычисляется для любого значения М.
  4. Для любого данного значения хэш-кода h вычислительно невозможно найти M такое, что Н(M)=h.
  5. Для любого данного М вычислительно невозможно найти М′ ≠ M такое, что H(M)=H(M′).
  6. Вычислительно невозможно найти произвольную пару (M,M′) такую, что H(M)=H(M′).

Первые три свойства требуют, чтобы хэш-функция создавала хэш-код для любого сообщения.

Четвертое свойство означает, что хэш-функция должна обладать свойством односторонности: легко создать хэш-код по данному сообщению, но невозможно восстановить сообщение по хэш-коду. Это свойство важно, если для аутентификации с помощью хэш-функции используется секретное значение. Само секретное значение может не посылаться, тем не менее, если хэш-функция не является односторонней, противник может легко раскрыть секретное значение следующим образом. Перехватив передаваемое сообщение, атакующий получает сообщение М и хэш-код h=Н(S||M). Если атакующий может инвертировать хэш-функцию, то он получает S||M=H–1(h). Так как атакующий теперь знает и М, и S||M, получить S совсем просто.

Пятое свойство гарантирует, что невозможно найти другое сообщение, чье значение хэш-функции совпадало бы со значением хэш-функции данного сообщения. Это предотвращает подделку сообщения, когда в качестве аутентификатора используется защищенный от изменения хэш-код. Предположим, что противник может прочитать сообщение и, следовательно, вычислить его хэш-код. Но так как противник не знает секретного ключа, он не имеет возможности изменить сообщение так, чтобы получатель этого не обнаружил. Если данное свойство не выполняется, атакующий может выполнить следующую последовательность действий: перехватить сооб-щение и его зашифрованный хэш-код, вычислить хэш-код сообщения, со-здать альтернативное сообщение с тем же самым хэш-кодом, заменить ис-ходное сообщение на поддельное. Поскольку хэш-коды этих сообщений совпадают, получатель не обнаружит подмены.

Хэш-функция, которая удовлетворяет первым пяти свойствам, называется простой или слабой хэш-функцией. Если кроме того выполняется шестое свойство, то такая функция называется сильной хэш-функцией. Шестое свойство защищает против класса атак, известных как атака "день рождения".

"Парадокс дня рождения"

Так называемый "парадокс дня рождения" состоит в следующем.

Первая задача. Каким должно быть число k, чтобы для данного значения X и значений Y1, …, Yk, каждое из которых принимает значения от 1 до n, вероятность того, что хотя бы для одного Yi выполнялось равенство X=Y

P (X = Y) ≥ 0.5

Для одного значения Y вероятность того, что X=Y, равна 1/n.

P (X = Y) = 1/n

Соответственно, вероятность того, что X ≠ Y, равна 1 – 1/n.

P (X ≠ Y) = 1 – 1/n

Если создать k значений, то вероятность того, что ни для одного из них не будет совпадений, равна произведению вероятностей, соответствующих одному значению, т.е. (1 – 1/n)k.

Следовательно, вероятность по крайней мере одного совпадения равна

P (X = Yi) = 1 – (1 – 1/n)k

По формуле бинома Ньютона

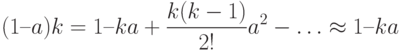
(1 – a)k = 1 – ka + \frac {k(k-1)} {2!} a^2 - … \approx 1 – ka
1 – (1 – k/n) = k/n = 0.5
k = n/2

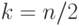
Таким образом, для хэш-кода длиной m бит достаточно выбрать 2m-1 сообщений, чтобы вероятность совпадения хэш-кодов была больше 0,5.

Теперь рассмотрим вторую задачу. Обозначим P(n,k) вероятность того, что в множестве из k элементов, каждый из которых может принимать n значений, есть хотя бы два с одинаковыми значениями. Чему должно быть равно k, чтобы P(n,k) была бы больше 0,5?

Число различных способов выбора элементов таким образом, чтобы при этом не было дублей, равно

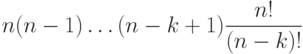
n (n-1) … (n-k+1) \frac {n!} {(n-k)!}

Всего возможных способов выбора элементов равно

n^k

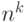
Вероятность того, что дублей нет, равна

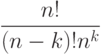
\frac {n!} {(n-k)! n^k}

Вероятность того, что есть дубли, соответственно равна

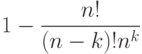
1 - \frac {n!} {(n-k)! n^k}
P (n, k) = 1 – n! / ((n-k)! \times n^k) = 1 – (n \times (n-1) \times … \times (n-k-1)) / n^k = 1 – [ (n-1)/n \times (n-2)/n \times … \times (n-k+1)/n] = 1 – [( 1- 1/n) \times (1 – 2/n) \times … \times (1 – (k-1)/n)]

Известно, что Если хэш-код имеет длину m бит, т.е. принимает 2m значений, то

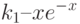
k_1 – x \leg e^-^x
P (n, k) > 1 – [e^-1^/^n \times e^-^2^/^n \times … \times e^-^k^/^n]
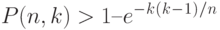
P (n, k) > 1 – e^-^k^(^k^-^1^)^/^n
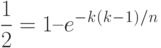
\frac 1 2 = 1 – e^-^k^(^k^-^1^)^/^n
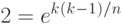
2 = e^k^(^k^-^1^)^/^n
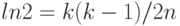
ln 2 = k (k-1) / 2n
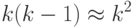
k (k-1) \approx k^2
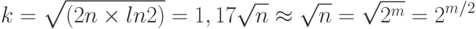
k = \sqrt {(2n \times ln 2)} = 1,17 \sqrt n \approx \sqrt n = \sqrt {2^m} = 2^m^/^2

Подобный результат называется "парадоксом дня рождения", потому что в соответствии с приведенными выше рассуждениями для того, чтобы вероятность совпадения дней рождения у двух человек была больше 0,5, в группе должно быть всего 23 человека. Этот результат кажется удивительным, возможно, потому, что для каждого отдельного человека вероятность того, что с его днем рождения совпадет день рождения у кого-то другого в группе, достаточно мала.

Вернемся к рассмотрению свойств хэш-функций. Предположим, что используется 64-битный хэш-код. Можно считать, что это вполне достаточная и, следовательно, безопасная длина для хэш-кода. Например, если защищенный хэш-код h передается с соответствующим незашифрованным сообщением М, то противнику необходимо будет найти М ′ такое, что

Н (М′) = Н (М)

для того, чтобы подменить сообщение и обмануть получателя. В среднем противник должен перебрать 263 сообщений для того, чтобы найти другое сообщение, у которого хэш-код равен перехваченному сообщению.

Тем не менее, возможны различного рода атаки, основанные на "парадоксе дня рождения". Возможна следующая стратегия:

  1. Противник создает 2m/2 вариантов сообщения, каждое из ко-торых имеет некоторый определенный смысл. Противник под-готавливает такое же количество сообщений, каждое из которых является поддельным и предназначено для замены насто-ящего сообщения.
  2. Два набора сообщений сравниваются в поисках пары сообщений, имеющих одинаковый хэш-код. Вероятность успеха в соответствии с "парадоксом дня рождения" больше, чем 0,5. Если соответствующая пара не найдена, то создаются дополни-тельные исходные и поддельные сообщения до тех пор, пока не будет найдена пара.
  3. Атакующий предлагает отправителю исходный вариант сообщения для подписи. Эта подпись может быть затем присоединена к поддельному варианту для передачи получателю. Так как оба варианта имеют один и тот же хэш-код, подпись будет соответствовать обоим сообщениям. Противник подписал поддельное сообщение, не зная при этом ключа, защищающего хэш-код.

Таким образом, если используется 64-битный хэш-код, то для подбора двух сообщений с одинаковым хэш-кодом в среднем необходимо перебрать 232 сообщений.

Вследствие этого длина хэш-кода должна быть достаточно большой. Длина, равная 64 битам, в настоящее время не считается безопасной. Пред-почтительнее, чтобы длина составляла не менее 100 битов.

Дальше >>
< Лекция 2 || Лекция 3: 123456 || Лекция 4 >

Вопросы и ответы

вопросов: 0