Определения, структура и развитие систем ИИ

Каждое из направлений ИИ имеет свои сильные и слабые стороны. Многогранность явления ИИ говорит о том, что не существует одного-единственного наилучшего способа для решения широкого спектра задач ИИ. Оптимальные решения могут быть достигнуты на базе комбинирования нескольких подходов. Например, разработки в области символьного ИИ лежат в истоках такого фундаментального направления в области ИИ как NLP (Natural Language Processing, обработка естественного языка), которое в последнее время активно развивается, опираясь на технологии глубокого обучения. Все чаще возникают проекты, в которых речь идет об интеграции символьных и субсимвольных подходов для обеспечения объяснимости ИИ-решений. Прежде чем привести примеры подобных решений, напомним читателю более подробно о сути коннекционистских подходов в создании ИИ.

Коннекционизм

Коннекционизм - от английского слова Connect (соединять) - это направление ИИ, которое исходит из предположения, что ментальные способности человека и, в частности, способность к обучению можно объяснить и имитировать на основе сложноорганизованной сети связанных между собой (соединенных определенным образом) одинаковых относительно простых элементов.

Одним из центральных направлений коннекционизма является моделирование интеллекта с помощью искусственных нейронных сетей, состоящих из нейронов и синапсов (связей между нейронами). Механизм работы искусственных нейронов заимствован из живой природы. Последние были созданы в результате наблюдения за процессами, происходящими в мозге живых организмов. Заметим, что сам термин "нейрон", используемый в понятии "искусственные нейронные сети" (ИНС), был заимствован из биологии. Представление о том, что развитие и обучение человека базируется на свойствах нейронов мозга устанавливать связи, не ново, согласно данным [39] данная идея была высказана еще в 1932 г. психологом из Колумбийского университета (Нью-Йорк) Эдвардом Торндайком.

Как известно из биологии, нервные клетки при определенном воздействии могут переходить в активированное состояние. Сигналы по нервным волокнам передаются в виде коротких импульсов от клетки к клетке, достигают нервных клеток в мышцах, что приводит к возбуждению мышечных волокон и, соответственно, к движению животного или человека.

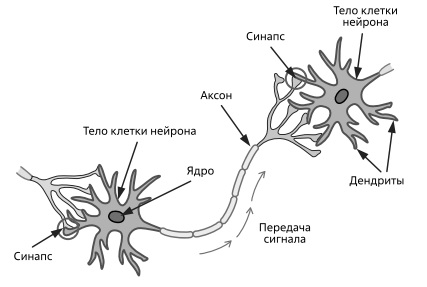
Каждая нервная клетка состоит из трех частей: из тела, нескольких ветвистых отростков (дендритов) и протяженного нервного волокна (аксона), длина которого может составлять от нескольких миллиметров до десятков сантиметров (рис. 1.23).

Рис. 1.23. Упрощенная схема передачи сигнала в биологических нейронах

Нервные клетки взаимодействуют между собой в местах стыка (синапсах), где встречаются аксон пресинаптического нейрона и дендрит постсинаптического нейрона. Дендриты являются входными каналами для нервных импульсов, поступающих через аксоны от других нейронов. Эти импульсы могут либо возбуждать (увеличивать), либо подавлять (уменьшать) мембранный потенциал тела нейрона, который со временем возвращается к своему нормальному значению. Если количество возбуждающих импульсов превышает пороговое значение, то нейрон сам генерирует импульс.

Взаимодействующие между собой посредством передачи возбуждений нейроны формируют нейронные сети.

Как будет показано далее, ИНС используют некоторую аналогию с работой живых нервных клеток.

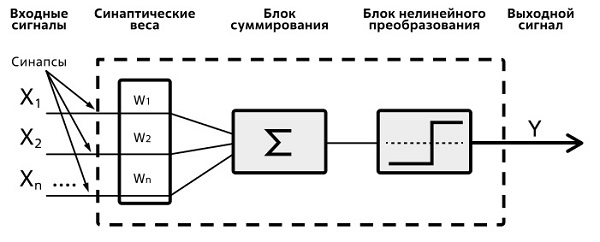
Основополагающей работой, заложившей фундамент для создания искусственных моделей нейронов и нейронных сетей, явилась работа Уоррена С. Мак-Каллока и Вальтера Питтса "Логическое исчисление идей, относящихся к нервной активности", опубликованная в 1943 г., в которой была предложена модель формального нейрона. Однако прошло более 10 лет, прежде чем появился нейрон Розенблатта, в котором использовалось суммирование входящих сигналов, умноженных на соответствующие числовые значения (синаптические веса) - рис. 1.24.

Рис. 1.24. Схема формального нейрона Розенблатта

Несложно проследить сходство схемы, показанной на рис. 1.24, и рисунка 1.24. Модель, прообразом которой является биологический нейрон, представляет собой устройство, имеющее несколько входов (синапсы) и один выход (аксон).

На вход подаются сигналы 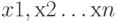. Каждому входу ставится в соответствие некоторый весовой коэффициент .

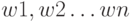Попадая в нейрон, сигналы умножаются на соответствующие веса и складываются между собой (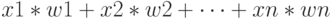 - линейное преобразование). Сложение сигналов, поступающих по синаптическим связям, осуществляется в сумматоре (рис. 1.24).

Известно, что последовательное применение нескольких линейных преобразований эквивалентно одному линейному преобразованию. Если бы модель нейрона ограничивалась одним сумматором, то объединение множества нейронов в сеть было бы эквивалентно одному нейрону. Для того чтобы нарушить это правило, в модель нейрона добавляется нелинейный преобразователь (который реализует нелинейную функцию, которая называется функцией активации).

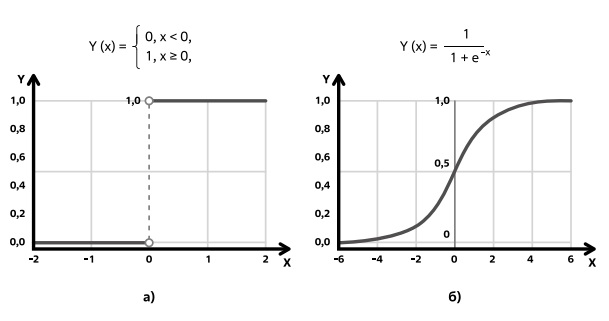
В рассмотренной модели использовалась пороговая функция активации (ступенчатая функция), которая показана на рис. 1.25 (а). Если суммарный сигнал превышает заданный порог активации, то нейрон возбуждается (активируется) и выдает на выходе 1, иначе выдается 0.

Определенным недостатком (ограниченной гибкостью) модели Уоррена Мак-Каллока являлся именно вид переходной функции (пороговый) - если значение вычисленного суммарного сигнала даже незначительно не достигает заданного порога, то выходной сигнал не формируется.

Такая функция подходит для бинарной классификации, но не подходит, когда для классификации требуется большее число нейронов (количество возможных классов больше двух). То есть если возникает задача, в которой возможно несколько ответов, или нам нужно вероятностное решение, например, с вероятностью 70% это один класс, а с вероятностью 30% - другой.

Впоследствии были реализованы модели нейрона с различными функциями активации. В частности, наиболее широкое использование получила сигмоида - гладкая монотонно возрастающая нелинейная функция, которая ограничена двумя горизонтальными асимптотами, что обеспечивает нормализацию выходного значения нейрона (рис. 1.25 б ) в диапазоне от 0 до 1.

По сути, нейрон представляет собой элементарный вычислитель, характеризующийся входным/ выходным состоянием и функцией активации.

Рис. 1.25. Ступенчатая функция (а) и сигмоидная (б)

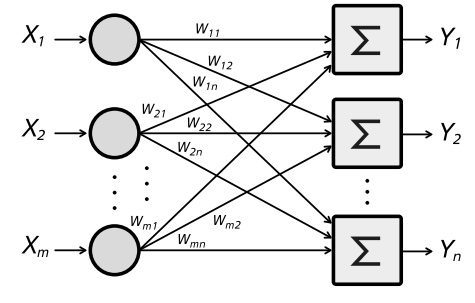
На основе элементарных вычислителей, каждый из которых получает сигналы и посылает другим вычислителям, составляются ИНС разной топологии. Самая простая однослойная сеть показана на рис. 1.26.

Рис. 1.26. Однослойная нейронная сеть

Здесь сигналы от входного слоя сразу подаются на выходной слой по связям, каждой из которых устанавливается свой весовой коэффициент.

С помощью подобной сети можно построить работу простейших автоматов. Например, на рис. 1.27 показан автомат (гусеничный робот с тремя датчиками света), реагирующий на положение источника света.