|
Мне нужно изучить математическую статистику с нуля для обработки данных на компьютере. Читаю уже вторую лекцию, но пока ничего даже отдалённо близкого к моей цели не нахожу. Есть ли математическая статистика в дальнейших лекциях? Или я зря теряю время на изучение этого курса? У меня крайне ограниченный временной срок - я не могу терять время на самостоятельную проверку моего вопроса посредством изучения данного курса. |
Средние величины в статистике
6.2. Средняя гармоническая
Средняя гармоническая величина является модифицированной формой средней арифметической. Она применяется в тех случаях, когда неизвестны значения частот у вариант ряда, зато имеются для каждого xi произведения этих вариант на соответствующие им частоты, т.д. ![[F_{i} = x_{i}' f_{i}]](/sites/default/files/tex_cache/fa45d1f5ada7f835183733109554cdb2.png) . Величиной Fi может быть, например, товарооборот по видам товаров при расчете их средней цены; фонд заработной платы по отдельным категориям работников при расчете средней заработной платы и т.д. Ситуаций, когда нам известны не частоты, а произведения частот на соответствующие им варианты при расчете средней величины, более чем достаточно.
. Величиной Fi может быть, например, товарооборот по видам товаров при расчете их средней цены; фонд заработной платы по отдельным категориям работников при расчете средней заработной платы и т.д. Ситуаций, когда нам известны не частоты, а произведения частот на соответствующие им варианты при расчете средней величины, более чем достаточно.
Формула средней гармонической взвешенной имеет следующий вид:
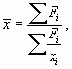
где Fi - произведения вариант на соответствующие им частоты;
xi - варианты.
Если мы для каждой варианты рассчитаем частоту как 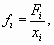 то формула средней гармонической взвешенной превратится в формулу для расчета средней арифметической взвешенной:
то формула средней гармонической взвешенной превратится в формулу для расчета средней арифметической взвешенной:
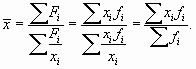
Пример 6.5. Вернемся к примеру 6.2, где рассчитывалась средняя заработная плата 20 работников малого предприятия. Предположим, что изначально были известны данные об уровне заработной платы для каждой группы работающих и начисленный им фонд заработной платы. Тогда для расчета средней заработной платы необходимо определить численность работающих в каждой группе. Для этого разделим фонд заработной платы каждой группы работающих на их уровень заработной платы (см. графу 3 в таблице). Тогда, разделив общий фонд заработной платы на общую численность работающих, получим их среднюю заработную плату.
| Исходные данные | Расчетный показатель | |
|---|---|---|
| заработная плата, руб. | фонд заработной платы, руб. | численность работающих, чел. |
| 1 | 2 | 3 |
| xi | Fi | Fi / xi |
| 5 950 | 35 760 | 6 |
| 6 790 | 54 320 | 8 |
| 7 000 | 42 000 | 6 |
| Итого | 132 080 | 20 |

Как видим, и в первом, и во втором случае расчет производился по одной и той же логической формуле

но использовались разные формулы для расчета, поскольку отличались исходные данные.
Если произведения вариант на соответствующие им частоты равны между собой, т.д. F1 = F2 = F3 = ... = Fn, то можно применять среднюю гармоническую простую, рассчитываемую по следующей формуле:

где п - число единиц в совокупности.
Пример 6.6. Предприятием были выделены одинаковые денежные суммы на приобретение акций двух видов, при этом цена акции вида "А" составляла 1000 руб., "В" - 1800 руб. Рассчитаем среднюю цену приобретения акций:

Поясним расчет. Мы знаем, что логическая формула для расчета средней цены приобретения одной акции такова:

Однако неизвестно, сколько было куплено акций каждого вида. Поэтому средняя арифметическая здесь не может быть использована.
Кроме того, мы знаем, что на покупку каждого вида акций была выделена одна и та же сумма. Обозначим ее через С. Тогда общая сумма, выделенная на покупку двух видов акций, будет равна 2С, а количество купленных акций каждого вида можно рассчитать следующим образом:
- для вида "А": C/1 000;
- для вида "В": С/1 800
Если подставить эти значения в логическую формулу, то неизвестная величина С (сумма, выделенная на приобретение каждого вида акций) сократится, и расчет действительно будет проведен по формуле средней гармонической простой:
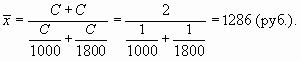
6.3. Средняя геометрическая
Для расчета среднего коэффициента или темпа роста статистического показателя используется формула средней геометрической.
Для несгруппированных данных (при отсутствии частот) или для сгруппированных данных с равными частотами применяется средняя геометрическая простая
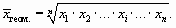
Для сгруппированных данных с неравными частотами применяется средняя геометрическая взвешенная
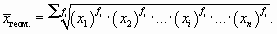
Примеры расчета средней геометрической будут рассмотрены в гл. 9.
6.4. Средняя квадратическая и другие степенные средние
Если подставить в формулу средней степенной m = 2, то получим среднюю квадратическую:
взвешенную (для сгруппированных данных):
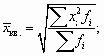
простую (для несгруппированных данных):

Средняя квадратическая величина широко применяется при оценке вариации признака, при изучении взаимосвязи явлений. Кроме того, прикладное значение имеет расчет степенных средних и более высоких порядков, например при изучении характеристик распределения случайных величин. Формулы для их вычисления получаются при подстановке в качестве m соответствующего показателя степени.
Правило мажорантности степенных средних состоит в том, что при расчете по одним и тем же данным между числовыми значениями средних, исчисленных по разным формулам, всегда сохраняется следующее неравенство:

