|
Добрый день! Подскажите пжл, не разобралась, обучение все платное? Мне сказали бесплатное есть... |
Совершенная конкуренция
7.2.2. Максимизация прибыли и правило MC = MR
Выбор принципиального варианта поведения (максимизация прибыли, минимизация убытков, временное прекращение производства) представляет собой лишь первый шаг фирмы в оптимизации своего положения на рынке. Следующий шаг состоит в точном установлении того объема производства, который максимизирует прибыль или (при менее благоприятных условиях) минимизирует убытки.
В принципе это может быть сделано путем прямого сравнения валового дохода и валовых издержек, как на графике 7.7. Маленькие фирмы, не имеющие мощных бухгалтерских подразделений, часто именно так и поступают. Они чисто опытным путем перебирают соотношения издержек и доходов при разных объемах производства и останавливаются на том из них, который обеспечивает наилучший финансовый результат.
Более точным способом определения оптимального размера производства является сравнение предельного дохода (MR) и предельных издержек (MC) - см. рис. 7.7.
Правило MR = MC
Увеличение выпуска продукции повышает прибыль только в том случае, если доход от продажи дополнительной единицы продукции превышает издержки производства данной единицы, т.е. если MR > MС. На рис. 7.7 этому условию соответствуют объемы выпуска А, В, С. Дополнительные прибыли, получаемые в результате выпуска этих единиц, выделены на нем жирными линиями.
Напротив, когда издержки, связанные с выпуском еще одной единицы продукции выше приносимого за счет ее реализации дохода (MR < MC), то, произведя соответствующую порцию товара фирма лишь сокращает свою прибыль или увеличивает убытки (см. точки D, E, F; жирно выделены дополнительные убытки).
Очевидно, что в этих условиях максимальная прибыль (или минимальные убытки) будет достигнута при том объеме производства (на рис. 7.7 точка О), где кривая предельных издержек в своем возрастании пересечет кривую предельного дохода, т.е. сравняется с ней (MR = MC). Действительно, пока MR > MC, увеличение производства, приближающее его к точке О, дает все большую прибыль. Когда же после пересечения кривых устанавливается соотношение MR < MC, к увеличению прибыли ведет, наоборот, сокращение производства. Другими словами, прибыль растет при приближении к точке равенства предельных издержек и дохода с любой стороны. А следовательно, максимум прибыли достигается в самой точке.
Эту закономерность в экономической науке принято называть правилом MR = MC. Согласно ему, максимизация прибыли (минимизация убытков) достигается при объеме производства, соответствующем точке равенства предельного дохода и предельных издержек. Правило MR = MC справедливо не только для условий совершенной конкуренции, но и для других типов рынка.
увеличить изображение
Рис. 7.8. Оптимизация объема производства в условиях максимизации прибыли (а), минимизации убытков (б), остановки производства (в)
Правило P = MC
В условиях совершенной конкуренции предельный доход равен цене товара. Поэтому правило MR = MC может быть представлено и в иной форме: P = MR = MC, или Р = МС.
То есть в условиях совершенной конкуренции максимизация прибыли (минимизация убытков) достигается при объеме производства, соответствующем точке равенства предельных издержек и цены.
На рис. 7.8 правило MR = MC применено к процессу выбора оптимального объема производства для всех трех важнейших рыночных ситуаций.
Выбор оптимального объема производства
Рис 7.8 а, в частности, показывает, как происходит выбор в условиях максимизации прибыли. Максимизирующая прибыль фирма устанавливает объем своего производства на уровне Q0, соответствующем точке пересечения кривых MR и MC (на графике точка О).
Обратим особое внимание на то, что объем производства Q0 в случае максимизации прибыли больше объема производства  , который соответствовал бы минимальному уровню средних общих издержек, т.е. технологическому оптимуму производства. Понятен и экономический смысл этого.
, который соответствовал бы минимальному уровню средних общих издержек, т.е. технологическому оптимуму производства. Понятен и экономический смысл этого.
В точке  достигается максимальная прибыль в расчете на единицу продукции. На графике хорошо видно, что именно здесь расстояние между кривыми АТС и Р наибольшее. Однако фирма максимизирует не удельную прибыль на единицу продукции, а валовый объем прибыли от всего производства. Поэтому ей нет смысла отказываться от выпуска единиц продукции, лежащих между
достигается максимальная прибыль в расчете на единицу продукции. На графике хорошо видно, что именно здесь расстояние между кривыми АТС и Р наибольшее. Однако фирма максимизирует не удельную прибыль на единицу продукции, а валовый объем прибыли от всего производства. Поэтому ей нет смысла отказываться от выпуска единиц продукции, лежащих между  и
и 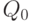 . Пусть в расчете на единицу продукции прибыли для них несколько ниже, но вклад в увеличение валовой прибыли внесут и они. Ведь здесь действует неравенство MR > MC, а значит, фирма выигрывает от выпуска каждой единицы дополнительной продукции.
. Пусть в расчете на единицу продукции прибыли для них несколько ниже, но вклад в увеличение валовой прибыли внесут и они. Ведь здесь действует неравенство MR > MC, а значит, фирма выигрывает от выпуска каждой единицы дополнительной продукции.
На
рис.
7.8 б показана ситуация минимизации убытков. Фирма и в данном случае ориентируется на правило MR = MC, избирая объем производства 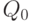 . Однако на сей раз он оказывается ниже технологически оптимального уровня
. Однако на сей раз он оказывается ниже технологически оптимального уровня  .
.
Другими словами, при пониженном уровне цен (точнее, когда они находятся ниже точки безубыточности) технологический оптимум становится экономически недостижимым. Эту закономерность в ходе затяжного кризиса в нашей стране испытали на себе многие отечественные предприятия: низкий уровень спроса заставляет их недоиспользовать свои производственные мощности.
Первое ограничение правила MR = MC
Одновременно на рис. 7.8 б удобно проследить закономерность, свойственную не только случаю минимизации убытков, но и другим вариантам поведения фирмы на рынке. Благодаря сравнительно низкому положению кривой Р на нем хорошо видно, что кривые MR и MC имеют не одну, а две точки пересечения.
Уточнение правила MR = MC состоит в том, что оно относится только ко второму пересечению кривых. Выбор производства на уровне первого пересечения MR и MC, напротив, не обеспечивает оптимизации производства. Дело в том, что первое пересечение находится на нисходящей ветви U-образной кривой МС. И по мере увеличения производства в районе этой точки оно становится все более выгодным: до объема выпуска 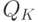 предельные издержки от выпуска очередной единицы выше предельного дохода, но сразу после превышения этого объема предельный доход начинает превышать издержки. А следовательно, как и во всех случаях, когда MR > MC, фирме надо наращивать объем производства.
предельные издержки от выпуска очередной единицы выше предельного дохода, но сразу после превышения этого объема предельный доход начинает превышать издержки. А следовательно, как и во всех случаях, когда MR > MC, фирме надо наращивать объем производства.
Второе ограничение правила MR = MC
Наконец, при третьем (см.
рис.
7.8 в) принципиальном варианте поведения, т.е. при остановке производства, правило MR = MC не применимо вообще. Прекращение производства в краткосрочном периоде целесообразно, если 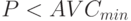 . Как было показано ранее (см.
рис.
7.6), в этом случае любой, кроме нулевого, объем производства вызывает убытки, превышающие величину постоянных издержек. Поэтому правильный выбор состоит в остановке производства, а не в выпуске продукции. Не оптимизируют финансовых результатов, в частности, и
. Как было показано ранее (см.
рис.
7.6), в этом случае любой, кроме нулевого, объем производства вызывает убытки, превышающие величину постоянных издержек. Поэтому правильный выбор состоит в остановке производства, а не в выпуске продукции. Не оптимизируют финансовых результатов, в частности, и 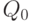 , соответствующее MR = MC.
, соответствующее MR = MC.
Положение части кривой MC ниже кривой MR в такой ситуации свидетельствует лишь о том, что несколько единиц продукции (скажем, с шестой по десятую деталь) можно произвести с издержками более низкими, чем уровень цены. Но вся изготовленная продукция при любом положительном объеме выпуска (будь то все шесть, все восемь или все десять деталей) производится со столь большими издержками, что они не могут быть покрыты не только полностью, но даже и в переменной своей части, за счет доходов от продажи.
Другими словами, второе ограничение правила MR = MC состоит в том, что оно не применимо при уровнях цен, лежащих ниже минимального значения средних переменных издержек.


