|
Курс Технология блокчейн и Биткоин Лекция 1. Раздел: Сравнение процедуры традиционной банковской онлайн транзакции и транзакции в сети Биткоин. Сравнение не убедительное. В приведенном примере оплаты за ритейл-услугу (покупка чашки кофе) получается, что подтверждения транзакции в сети Биткойн нужно ждать час, а при использовании традиционного POS-терминала подтверждение мгновенное (а при использовании банком системы мгновенных платежей, средства будут зачислены на счет продавца в другой банк почти мгновенно). При этом, покупатель при блок-чейне оплачивает комиссии сам, т.е. сумма на ценике и сумма перевода разные, а при использовании POS-терминала сколько на ценике, столько и списывается. Чем в приведенном примере для участников транзакции использование блок-чейн отличается от использования простых электронных кошельков? Не могу отделаться от ощущения, что блк-чейн - очередная "мода", позвляющая ИТшникам полчать финансирование.
|
Криптографические ключи, адреса, кошельки
Почему это важно?
Цель: Сформировать понимание важности криптографических алгоритмов для криптовалют.
Право владения токенами, в том числе, биткоинами устанавливается через криптографические (цифровые) ключи, Биткоин-адреса и цифровые подписи. Закрытые криптографические ключи не перемещаются по сети. Они генерируются и хранятся пользователями в специализированном клиенте (кошельке). Цифровые ключи в кошельке пользователя являются абсолютно независимыми от протокола Биткоин, генерируются и управляются с помощью программного обеспечения кошелька пользователя без обращений к блокчейну или к сети Интернет. Благодаря такой стратегии управления ключами становятся возможными многие из важнейших свойств сети Биткоин, в том числе децентрализованные консенсус и контроль, подтверждение владения, и модель безопасности, основанная на математическом (криптографическом) доказательстве.
Каждая транзакция в сети Биткоин должна быть подписана подлинной электронной подписью, которая может быть получена только при наличии валидных цифровых криптографических ключей. Следовательно, любой, получивший копии данных ключей, имеет точно такой же контроль над средствами, ассоциированными с этой учетной записью, как и ее истинный владелец.
Ассиметричная схема шифрования подразумевает наличие криптопары: частного (закрытого) и публичного (открытого) ключей. Публичный ключ можно сравнить с номером банковского счета, тогда приватный ключ выполняет функцию PIN-кода или подписи на банковском чеке, обеспечивая полный доступ к учетной записи. Эти цифровые ключи почти никогда не попадаются на глаза пользователям сети Биткоин. В основном, они хранятся в файлах бумажника, а манипуляции ключами выполняет программное обеспечение кошелька – разумеется по инициативе владельца.
Если рассматривать процедуру платежа, то в соответствующей транзакции фигурирует Биткоин-адрес получателя, являющийся фактически цифровым отпечатком открытого ключа. Сравним его с именем получателя денежных средств на банковском чеке.
В большинстве случаев биткоин-адрес формируется на основе публичного ключа. По крайней мере, это утверждение справедливо в отношении всех обладателей собственных аккаунтов. Забегая вперед скажем, что получателями средств могут быть сценарии. Их биткоин-адреса определяются по иной схеме.
Таким образом, в рамках сети Биткоин адреса обеспечивают анонимность пользователей. Не существует способа ассоциировать биткоин-адрес с конкретным физическим или юридическим лицом. Но эта анонимность поддерживается только в рамках сети Биткоин. Использование токенов на криптобиржах или магазинах, принимающих криптовалюту, в большинстве случае потребует стандартной идентификации владельца криптосредств. Из выше сказанного следует, что в отличие от стандартной схемы цифровой подписи даже публичный ключ не распространяется по сети и не передается другим пользователям. Вместо него для решения задач авторизации используются биткоин-адреса.
Криптография с открытым ключом
Цель: Определить "точки пересечения" ассиметричной криптографии и протокола Биткоин.
Криптография с открытым ключом была изобретена в 70-х годах прошлого века. Именно ассиметричные криптоалгоритмы традиционно стали использоваться в качестве математической основы при построении систем компьютерной и информационной безопасности. В процессе становления криптографии с открытым ключом было найдено несколько классов математических функций, получивших название односторонние. К ним, в частности, относятся возведение в степень простого числа, умножение эллиптических кривых и др. Необратимость означает, что прямые значения такого рода функций вычисляются достаточно просто, а вот обратные рассчитать практически невозможно. На основе односторонних функций разработано довольно много алгоритмов цифровых шифров и криптостойких электронных подписей.
В сети Биткоин для создания криптопары, контролирующей доступ к счету, используется умножение на эллиптических кривых. Так же, как и в других ассиметричных криптосистемах пара ключей состоит из закрытого ключа и производного от него, уникального открытого ключа. Публичный и приватный ключи однозначно связаны математическим соотношением. Такая связь обеспечивает возможность подписи сообщения приватным ключом с одной стороны, и последующую проверку правильности подписи при помощи публичного ключа, с другой. При этом приватный ключ не раскрывается. В платежных операциях открытый ключ используется для получения биткоинов (как основание для определения адреса), а с помощью закрытого ключа подписываются транзакции, предназначенные для траты имеющихся на балансе счета средств (на самом деле понятие баланса в привычном понимании в сети Биткойн не применяется). Фактически, любой пользователь, намереваясь потратить имеющиеся у него биткоины, должен опубликовать в сети свои открытый ключ и электронную подпись транзакции, полученную с помощью соответствующего закрытого ключа. После публикации этих данных любой участник сети (и, в первую очередь, майнеры) могут проверить правомочность совершаемых финансовых действий и признать транзакцию действительной. Сделка будет считаться совершенной после того как проверенная транзакция в составе очередного валидного блока будет включена в блокчейн.
Поскольку открытый ключ в любой момент может быть вычислен на основе закрытого ключа, некоторые кошельки хранят только приватные ключи.
Управление ключами в сети Биткоин
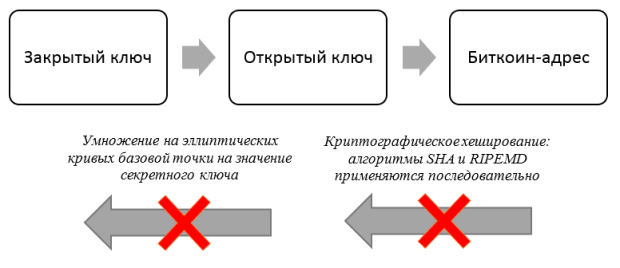
Цель: Сформировать понимания процессов преобразования цепочки криптографических преобразований: Закрытый ключ ? Открытый ключ ? Биткоин-адрес.
При создании биткоин-кошелька на компьютере создается специальный файл, содержащий в себе две записи: private key (закрытый ключ) и public key (открытый ключ). Обычно это что-то типа wallet.dat. И если закрытый ключ генерируется случайным образом, то открытый ключ создается путем криптографического преобразования закрытого ключа. Если быть точным в Биткойн-сети используется алгоритм эллиптической криптографии secp256k1 – вариация широкоизвестного Алгоритма Цифровой Подписи с Эллиптическими Кривыми (ECDSA).
Закрытый ключ - случайное число длиной в 256 бит, генерируемое для каждого счета пользователя. Чтобы доказать окружающим, что приватный ключ у пользователя имеется, и не раскрыть его при этом, вычисляется второе число —публичный ключ. Для этих целей как раз и используется криптосистема ECDSA. Преобразование это одностороннее, т.е. выполнение обратной операции - вычисление закрытого ключа по открытому – является практически невыполнимой задачей.
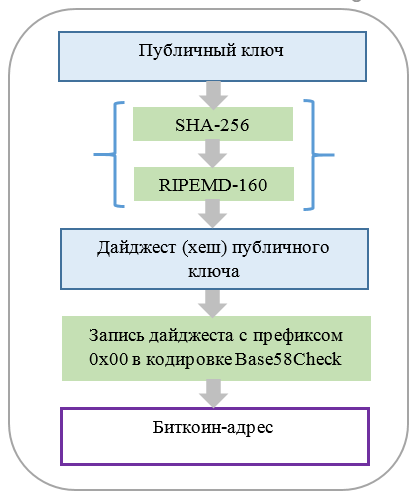
Наконец, есть еще и третье число: так называемый "адрес кошелька". Как и в любой другой системе адрес нужен для целей идентификации пользователей. Отправлять биткоины "на деревню, дедушке" конечно же в голову никому не придет. В принципе публичный ключ сам мог бы послужить адресом, более того, первый протокол платформы Bitcoin именно это и предполагал. Но достаточно быстро было принято решение перейти на другую схему вычисления адреса. Он стал короче по сравнению с ключами - всего 160 бит и, одновременно, безопасней. Адрес вычисляют на основе публичного ключа путем последовательного двукратного вычисления хеш-функций (сначала SHA-256, а затем RIPEMD-160).
Связь между криптопарой (закрытым и открытым ключами) и биткоин-адресом продемонстрирована на рисунке 2.1.
Рассмотрим эти вопросы подробнее.
Закрытые ключи
Цель: Сформировать четкое понимание процесса и развить практические навыки получения закрытых ключей в сети Биткоин.
Закрытый ключ — это просто число, взятое наугад. Только владелец закрытого ключа контролирует средства, связанные с определенным биткоин-адресом.
Секретный ключ используется для создания электронной подписи, необходимой в качестве неопровержимого доказательства права владения средствами в транзакции. Секретный ключ должен храниться в строжайшем секрете. Его несанкционированное копирование по сути означает передачу контроля над средствами в чужие руки.
Следует позаботиться о создании резервной копии секретного ключа. В случае его потери доступ к соответствующим средствам также будет утрачен. Они окажутся замороженными в блокчейне сети Биткоин навсегда. Не существует никакого легального способа ими воспользоваться. Ни у кого в целом мире, включая Сатоши Накомото.
Секретный ключ — это просто целое число. Можно сформировать валидный секретный ключ, прибегнув к дедовскому способу - подбрасыванию монеты. Правда подбрасывать ее придется 256 раз. Записав результаты этого эксперимента Вы получите двоичную запись случайного секретного ключа, который можно использовать в биткоин-кошельке. Разумеется, протокол платформы Биткоин предусматривает более современные способы генерации приватных ключей.
Задача осложняется тем, что большинство привычных инструментов генерации случайных чисел выдают, так называемые, псевдослучайные последовательности, не основанные на надежных источниках энтропии. Самый надежный способ состоит в использовании квантовых генераторов случайных бинарных последовательностей, примеры практической реализации которых уже известны. Основаны такие устройства на принципиально ином источнике случайности, чем большинство традиционных генераторов. А именно, квантовой неопределенности. Согласно фундаментальным законам квантовой механики, у электрона или другой частицы нет траектории, которую можно проследить. Есть лишь вероятность обнаружить частицу в той или иной области пространства. И подобную энтропию невозможно устранить даже теоретически. На самом деле такая неопределенность характерна не только для движения элементарных частиц, но и присуща, по сути, всем квантовым процессам. В обозримом будущем, наверняка, именно такие генераторы существенно снимут остроту проблемы. Но пока на практике прибегают к более предсказуемым, а потому ненадежным инструментам генерации случайных чисел.
Создание секретного ключа для платформы Биткоин, по сути, аналогично выбору числа в диапазоне от 1 до 2256 (на самом деле используется число, несколько меньшее чем 2256, верхняя граница диапазона задается числом n - 1, где n = 1,158 · 1077 - порядок эллиптической кривой, используемой в платформе Биткоин). Программное обеспечение сети Биткоин использует штатные генераторы случайных чисел, входящие в состав операционных систем. Как правило, генератор случайных чисел стандартной операционной системы инициализируется источником энтропии, исходящим непосредственно от пользователя. Обычно, это сводится к тому, что пользователю предлагается некоторое время шевелить мышкой. Далее к результату оцифровки сформированной траектории применяется хеш-функция SHA256, на выходе которой мы получаем 256-битное число. Остается только сравнить его с верхней границей n. Если полученное число меньше величины n - 1, тогда мы нашли подходящий закрытый ключ для вновь образуемого счета в сети Биткоин (сравнение нового значения с уже сформированными в сети закрытыми ключами не производится!).
Ниже приведен случайным образом сгенерированный секретный ключ (k) в шестнадцатеричном формате (64 шестнадцатеричных цифры):
1E88423A4ED27609A15A2616A2B0E8E52CED330AC530EDCC32C9FFC6A526AEDD
Отметим, что пространство возможных приватных ключей платформы Биткоин (от 1 до 2256) имеет колоссальные размеры. Если обратиться к более привычной для большинства людей десятичной системе счисления, то это примерно от 1 до 1077. По имеющимся оценкам видимая часть Вселенной состоит всего-то из 1080 атомов – вполне сравнимые объемы.
Отображение секретного ключа в виде числовой последовательности не всегда является удобным. Часто прибегают к более прогрессивному формату WIF (Wallet Import Format). Значение в таком формате получается довольно просто. Двоичную запись ключа предваряют специальным префиксом – числом 128 (0x80 в шестнадцатеричной системе счисления). Полученное значение записывают в формате Base58Check. О кодировке Base58Check чуть позже мы поговорим подробнее. Пока представим пример записи секретного ключа в формате WIF:
секретный ключ = 0a56184c7a383d8bcce0c78e6e7a4b4b161b2f80a126caa48bde823a4625521f секретный ключ в формате WIF = 5HtqcFguVHA22E3bcjJR2p4HHMEGnEXxVL5hnxmPQvRedSQSuT4.
Открытые ключи
Цель: Сформировать четкое понимание процесса получения открытых ключей в сети Биткоин.
Открытый ключ K получается из секретного путем одностороннего скалярного умножения на эллиптических кривых базовой точки на значение секретного ключа.
K = k · G,
где k — это приватный ключ, G — базовая точка,
Обратная операция вычисления k (нахождение дискретного логарифма) при известном K возможна только при помощи полного перебора k, т.е. весьма непродуктивной атаки типа "brute force". Прежде, чем мы перейдем к генерации публичных ключей немного поговорим о криптографии на эллиптических кривых.
Криптография на эллиптических кривых
Криптография на эллиптических кривых — это вид асимметричной криптографии или криптографии с открытым ключом, основанная на проблеме дискретного логарифмирования на эллиптических кривых.
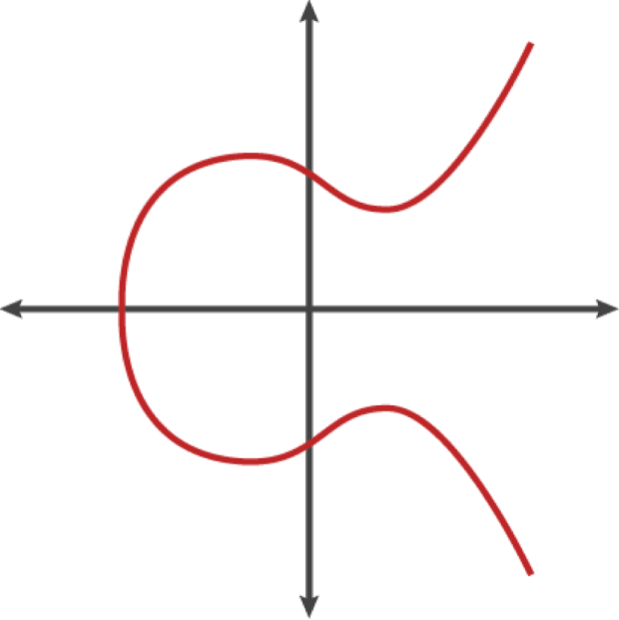
На рисунке 6 продемонстрирован пример эллиптической кривой, аналогичной той, которая используется в платформе Биткоин.
Эллиптические кривые обладают целым набором полезных свойств. Например, любая наклонная прямая, пересекающая эллиптическую кривую в двух точках, всегда будет пересекать ее также в третьей точке. Следующим фактом является то, что любая наклонная прямая, являющаяся касательной к кривой в одной из точек, обязательно пересечет кривую еще ровно в одной точке. Эти свойства окажутся востребованными в криптосистемах.
В сети Биткоин используется конкретная эллиптическая кривая и набор математических констант из стандарта под названием secp256k1 установленного Национальным Институтом Стандартов и Технологий (NIST).
Уравнение эллиптической кривой: y2 = x3 + 7
Определенной над полем y2 mod p = x3 + 7 (mod p)
Операция нахождения модуля простого числа р - (mod p) показывает, что эллиптическая кривая определена над конечным полем простого порядка p, где p = 2256 - 232 - 29 - 28 - 27 - 26- 24 - 1 является очень большим простым числом.
Простой модуль p = 2256 - 232 - 29 - 28 - 27 - 26 - 24 - 1 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
Базовая точка:
Х = 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798
Y = 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
Порядок = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141 - количество точек кривой над конечным полем.
В ECDSA секретный ключ — это случайное число между единицей и значением порядка.
Открытый ключ = секретный ключ · значение базовой точки.
Постараемся в этом разобраться подробнее.
Эллиптическая кривая над полем K — это кубическая кривая над алгебраическим замыканием поля K, задаваемая уравнением третьей степени с коэффициентами из поля K и "точкой на бесконечности". Одной из форм эллиптических кривых являются кривые Вейерштрасса
y2 = x3 + a*x + b
Для коэффициентов a = 0 и b = 7 (используемых в платформе Биткоин), график функции изображен на рисунке 2.2.
В эллиптической криптографии используется такая же кривая, но определенная над некоторым конечным полем.
y2 mod p = x3 + a*x + b (mod p)
Конечное поле в контексте эллиптической криптографии можно представить, как предопределенный набор целых, положительных чисел, которому должен принадлежать результат любого вычисления. Например, 11 mod 8 = 3. Здесь мы имеем конечное поле от 0 до 7, и все операции по модулю 8, над каким бы значением они ни осуществлялись, приведут к результату из этого диапазона.
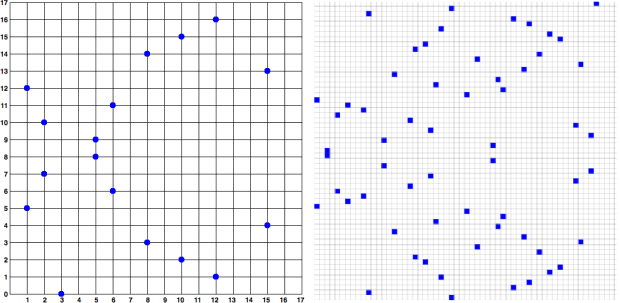
Поскольку эллиптическая кривая определена над конечным полем простого порядка, а не вещественных чисел, она выглядит как узор из точек, рассеянных в двух измерениях, что достаточно трудно визуализировать. Тем не менее, математика идентична математике эллиптической кривой в вещественных числах. В качестве примера, на рисунке 2.3 отображены эллиптические кривые над полем очень скромных конечных простых порядков (р = 17, р = 59), иллюстрирующая то, каким образом располагаются точки на координатной сетке. Эллиптическая кривая, используемая в криптосистеме платформы Биткоин, secp256k1 представляет собой гораздо более сложную совокупность точек, распределенных на неизмеримо большей координатной сетке.
при р = 17 и при р = 59
Эллиптическая кривая на множестве вещественных чисел (непрерывные числовые значения, в том числе и дробные) не позволяет получить однозначное соответствие (биекцию) исходных данных их образам (хешам). Чтобы не усложнять, и без того не простые, расчетные методы еще и округлением, для целей криптографии используются только точки с координатами из множества конечных полей. Исходя из этого, на эллиптической кривой берутся точки со значениями координат попадающими в конечное поле.
Вспомним основные свойства эллиптических кривых. И постараемся понять, как их можно использовать в криптографии.
Эллиптическая кривая над полем есть неособая кубическая кривая на проективной плоскости над алгебраическим замыканием поля, задаваемая уравнением 3-й степени с коэффициентами из поля и "точкой на бесконечности"
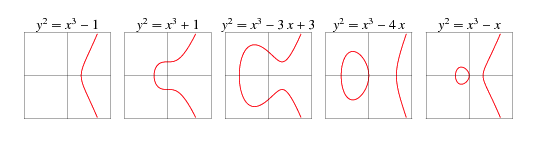
В зависимости от значений параметров a и b график данной функции может выглядеть по-разному:
Математики давно заинтересовались эллиптическими кривыми. Первые упоминания о них находят в трудах Диофанта. А в 17 веке, ее свойства исследовал Ньютон. Именно его труды послужили основой для формализации правил сложения точек на эллиптической кривой.
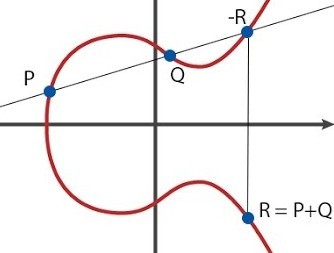
Пусть на некой эллиптической кривой f определены две точки P,Q ? f. Их суммой называется точка R ? f, которая в простейшем случае определяется следующим образом. Проведем прямую через точки P и Q. Пересечение этой прямой с кривой f даст нам точку -R. Отобразив точки -R симметрично относительно оси x, получаем искомую точку R, которую будем называть суммой P + Q = R.
Считаю необходимым отметить, что мы именно таким образом определяем операцию сложения. Попытка сложить точки согласно традиционного правила, то есть суммируя соответствующие координаты, даст совершенно другую точку, которая, скорее всего, не имеет ничего общего с точкой R и даже не лежит на кривой f.
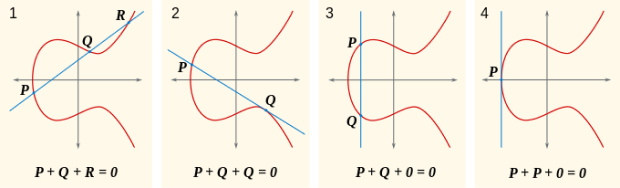
В случае, когда складываются две точки, имеющие координаты вида P(a, b) и Q(a, -b), прямая пройдет параллельно оси ординат (третья слева ситуация на Рисунке 2.6).
Как следует из рисунка, в этом случае отсутствует пересечение с кривой f в точке, которое мы называли -R. Для того, чтобы избежать подобной ситуации, введем так называемую точку в бесконечности (point of infinity), обозначаемую обычно О или просто 0. Установим, что в случае отсутствия пересечения P + Q = О.
Если P1 является точкой в бесконечности, тогда сумма Р1 + Р2 = Р2. Аналогично, если Р2 является точкой в бесконечности, тогда Р1 + Р2 = Р1. Данное свойство демонстрирует, как точка на бесконечности играет роль нуля в эллиптической математике.
Особый интерес для нас представляет вариант, когда мы хотим сложить точку саму с собой (вторая слева ситуация на рисунке 10, точка Q). В этом случае сначала проводится касательная к точке Q, а полученная точка пересечения отображается относительно оси ординат.
Оказывается, что операция сложения на эллиптических кривых ассоциативна. Следовательно, ( A + B ) + C = А + (B + C ). Т.е., мы можем написать A + B + C без скобок и такая запись будет восприниматься совершенно однозначно.
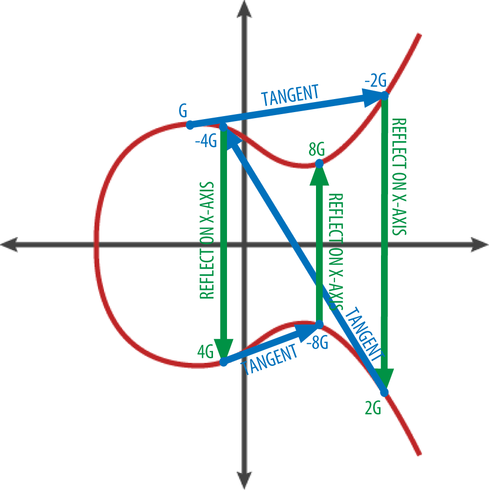
А теперь мы подошли к самому главному – умножению точки G на какое-то натуральное число k. В результате получим новую точку K = G · k, т.е., K = G + G + G + G + G + …, k раз. Алгоритм умножения точки на число на эллиптической кривой f проиллюстрирован на рисунке 2.7.
Таким образом, скалярное умножение на эллиптических кривых это тоже самое, что и суммирование точки G самой с собой k раз подряд. В свою очередь, каждое "удвоение" точки G является эквивалентом построения касательной к упомянутой точке, нахождения пересечения построенной прямой с эллиптической кривой и отображения найденной точки пересечения относительно оси абсцисс.
Создание открытого ключа
Цель: Сформировать практические навыки получения открытых ключей в сети Биткоин.
Пусть k — наш закрытый ключ, G — базовая точка, тогда открытый ключ K = k · G. То есть, фактически, открытый ключ — это некоторая точка, лежащая на кривой secp256k1. Поскольку, базовая точка одинакова для всех пользователей платформы Биткоин, закрытый ключ k при умножении на G всегда дает один и тот же открытый ключ – K.
Отметим два важных момента. Во-первых, операция вычисления открытого ключа определена однозначно, то есть конкретному закрытому ключу всегда соответствует ровно один единственный открытый ключ. Во-вторых, обратная операция является вычислительно трудной и, в общем случае, получить закрытый ключ из открытого можно только путем полного перебора первого – задача практически невыполнимая (по крайней мере, в настоящее время). На самом деле, точно также связаны открытый ключ владельца счета и биткоин-адрес (правда в этом случае результат достигается за счет необратимости хеш-функций). Именно поэтому биткоин-адрес (полученный из K) можно передавать кому угодно без риска дискредитировать закрытый ключ k и как результат - лишиться части своих криптозапасов.
Открытый ключ K определяется как точка на эллиптической кривой K = (х, у).
Если
k = 1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD, то
K = (х, у)
где,
x = F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A y = 07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB.
Таким образом, открытый ключ в алгоритмах электронной подписи, основанных на использовании эллиптических кривых, является координатами точки на этих самых кривых. Т.е., это два числа – координаты X и Y. На самом деле используется несколько вариантов записи открытого ключа. Пока мы остановимся на так называемом uncompressed формате - по 32 байта для каждой из осей координат. Чтобы не возникало путаницы, используется специальный префикс 04 (0x04 в шестнадцатеричной системе), в итоге получается 65 байт.
Например, для секретного ключа k = 0a56184c7a383d8bcce0c78e6e7a4b4b161b2f80a126caa48bde823a4625521f
публичный ключ будет выглядеть следующим образом:
045fbbe96332b2fc2bcc1b6a267678785401ee3b75674e061ca3616bbb66777b4f946bdd2a6a8ce419eacc5d05718bd718dc8d90c497cee74f5994681af0a1f842,
где первый байт = 04 – префикс, означающий, что мы имеем дело с открытым ключом.
На всякий случай, вспомним как работают стандартные алгоритмы электронной подписи, а немного позже отметим особенности, присущие их реализации в сети Биткоин.
Электронная подпись - это криптосистема, обеспечивающая решение следующих задач:
- контроль целостности электронных документов. Любое случайное или преднамеренное изменение содержимого документа автоматически сделает подпись недействительной.
- убедительное доказательство подлинности авторства документа. Поскольку доступ к закрытому ключу есть исключительно у его владельца, следовательно, только он может создать корректную электронную подпись. Рассуждая аналогичным образом, электронную подпись также можно использовать для обеспечения неотказуемости от авторства документа.
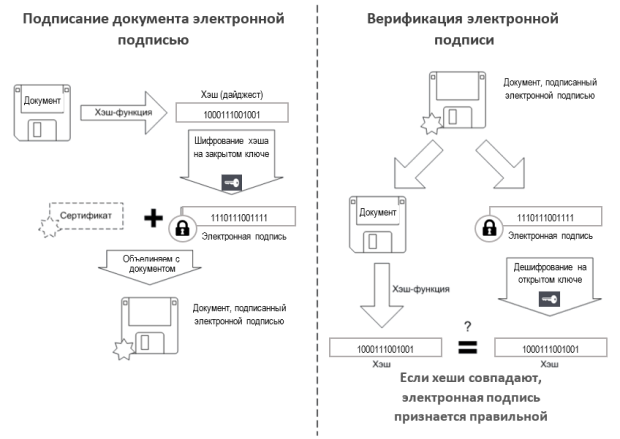
Есть говорить о технической стороне вопроса, то на практике превалируют решения, реализующие схемы с открытым ключом. Поэтому в качестве иллюстрации на рисунке 12 приведен именно ассиметричный алгоритм электронной подписи.
Процесс начинается с фазы подписания документа электронной подписью. В реальных системах для получения электронной подписи полный текст документа обычно не используется, иначе мы столкнемся с большими временными и аппаратными издержками. Как известно, ассиметричные криптосистемы предъявляют гораздо больше требований к аппаратным ресурсам и работают медленнее по сравнению с симметричными. Поэтому текст документа перед подписанием подвергается предварительному сжатию с помощью функции хеширования. Полученный результат называют дайджестом. Свойства хеш-функции гарантируют следующие качества дайджеста:
- Стандартные размеры - результат хеширования не зависит от объема текста на входе.
- Уникальность для любых уникальных наборов символов – исключена возможность формирования одинаковых хешей для разных массивов данных.
- Невозможность по его значению восстановить исходный текст – преобразование посредством хеш-функции является односторонним.
Затем дайджест шифруется на закрытом ключе лица, подписывающего документ. Результатом этой операции является собственно электронная подпись – специальный, цифровой реквизит документа. Сведения о владельце ключа и зашифрованный хеш помещаются в специальный контейнер, прикрепляемый к документу. Так же в документ (но уже в другой контейнер) вкладывается открытый ключ подписанта. Весь указанный массив информации (документ и два контейнера) далее отправляется адресату.
Верификация электронной подписи реализуется следующим образом. Вычисляется дайджест полученного документа. Параллельно с этим дешифруется с использованием открытого ключа подписанта блок электронной подписи из контейнера. Если они совпадут, тогда результат верификации признается успешным. Это означает, во-первых, что подпись подлинная (основание для такого решения – открытый ключ соответствует закрытому, хранящемуся только у лица, подписавшего документ) и, во-вторых, что после подписания текст документа не менялся (иначе бы вычисленный и полученный путем дешифрации дайджесты не совпали).
Наиболее известными алгоритмами создания электронной подписи являются:
- Криптосистема RSA, пригодная и для шифрования, и для электронной подписи. Такие популярные криптографические решения как PGP, S/MIME, TLS/SSL, IPSEC/IKE и ряд других построены на основе RSA.
- DSA (основан на вычислительной сложности исчисления логарифмов в конечных полях) и ECDSA (основан на аппарате эллиптических кривых) - алгоритмы с открытым ключом, являющиеся американскими стандартами электронной подписи.
- Схема Шнорра и др.
Биткоин-адреса
Цель: Сформировать четкое понимание процесса и развить практические навыки получения биткоин-адресов, включая подробное обсуждение кодировки Base58Check.
Решение использовать в качестве адреса хеш-функцию, а не открытый ключ основывалось на двух соображениях:
- Криптосистемы на эллиптических кривых уязвимы для модифицированного алгоритма Шора при решении задачи дискретного логарифма на эллиптических кривых. Это означает, что появившиеся в будущем квантовые компьютеры смогут получить закрытый ключ из открытого ключа. Публикуя открытый ключ только тогда, когда монеты были потрачены (и при условии, что адреса не используются повторно), такая атака потеряет смысл.
- С дайджестом ограниченного размера будет легче работать: печатать; встраивать его в небольшие носители информации, такие как QR-коды.
Биткоин-адрес представляет собой строку из цифр и символов латинского алфавита. Адреса, полученные на основе открытых ключей, начинаются с цифры 1 (так называемые pay-to-public-key hash адреса). Ниже приводится пример подобного биткоин-адреса:
1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy.
Чаще всего в качестве получателя средств в транзакциях Биткоин фигурирует именно биткоин-адрес. Если сравнить транзакцию в сети Биткоин с бумажным чеком, то адрес получателя явился бы тем, что мы пишем в строке "Получатель платежа". В качестве получателя на бумажном чеке может значиться название фирмы, учреждения, или даже указание обналичить чек. Именно возможность использования абстрактного имени в качестве получателя на бумажном чеке обеспечивает значительную гибкость чековым финансовым системам. Платформа Биткоин использует сходную абстракцию. Кроме упомянутых биткоин-адресов, определяющих владельца счета (т.е., обладателя соответствующей криптопары) в сети Биткоин адресатом может быть назначен некий сценарий, который определяет, кто может распоряжаться выходами транзакции (pay-to-script hash, такие адреса начинаются с цифры 3). Платформа Биткоин поддерживает также мульти-подписи, когда основной сценарий требует более одной подписи для доказательства права собственности и, следовательно, предоставления возможности распоряжения средствами, ассоциированными с подобным счетом. В общем случае мульти-подпись М-из-N, реализованная в сети Биткоин, требует для разблокирования выхода транзакции наличия M подписей из N возможных. Разумеется, М ? N.
Начнем с анализа самого простого случая, когда биткоин-адрес получается из публичного ключа с помощью односторонней криптографической функции хеширования. Заметим, что криптографические хеш-функции широко задействованы в реализации целого ряда принципиальных инструментов сети Биткоин: при создании биткоин-адресов или адресов сценариев, в алгоритме доказательства работы (Proof of work) в майнинге.
Адрес из публичного ключа получается в результате последовательного применения двух алгоритмов криптографического хеширования. А именно, Secure Hash Algorithm (SHA) и RACE Integrity Primitives Evaluation Message Digest (RIPEMD). Чтобы быть совсем точным, упомянем о том, что на первом этапе длина получаемого дайджеста составляет 256 бит (т.е., используется алгоритм SHA-256), а на втором – 160 бит (RIPEMD-160).
Процесс получения биткоин-адреса отображен на рисунке 13.
Кодировка Base58Check
Для записи биткоин-адреса почти всегда используется кодировка Base58Check, мощность алфавита которой составляет 58 символов. Назначение ее очень простое – представить последовательность байт в простом и удобочитаемом формате и максимально снизить при этом вероятность возможных опечаток или ошибок. Понятно, почему это важно. С биткоин-адресами работают люди, которым вообще свойственно ошибаться. При работе с большими, не имеющими традиционного смысла наборами символов вероятность ошибок резко возрастает. При этом, чтобы безвозвратно потерять средства, достаточно ошибиться всего лишь в одном символе адреса. Правда разработчики платформы Биткоин в свое время об этом подумали и предусмотрели несколько механизмов защиты от ошибок. И первый из них – это использование для записи адресов кодировки Base58Check. Заметим, что вторая по популярности криптовалюта Эфириум такой защиты не имеет, хотя и появилась позже.
Само по себе представление Base-64 используется для передачи бинарных данных в "символьных средах", наподобие электронной почты. Алфавит формата Base-64 состоит из 26 прописных букв, 26 заглавных букв, 10 цифр, и двух дополнительных символов, которые в различных вариациях могут меняться. В свою очередь кодировка Base58 — это подмножество Base64, использующее прописные и заглавные буквы, цифры, но из набора символов исключаются те, которые часто путают, а именно 0 (ноль), O (заглавная буква О), l (маленкая L), I (большая i). Не включены в алфавит и два выше упомянутых дополнительных символа.
Т.е., алфавит Base58 включает следующие символы:
123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz
От опечаток при наборе адреса призвана спасти кодировка Base58Check. Фактически это расширение строки, записанной с помощью Base58, путем добавления кода проверки ошибок. Четыре байта вычисленной контрольной суммы, полученной путем хеширования исходных данных, добавляются в конец числовой последовательности. Программное обеспечение кошелька вычисляет контрольную сумму сравнивает ее с контрольной суммой из вводимого в систему адреса. Если данные не совпадают, значит при вводе была допущена ошибка. Подобная проверка позволяет предотвратить отправку средств по несуществующему биткоин-адресу.
Предварительно к конвертируемым в формат Base58Check данным добавляется префикс (байт версии), обеспечивающий категоризацию типов данных. Префикс версии в кодировке Base58Check позволяет создавать различные форматы, легко различимые визуально по определенному набору символов в начале строки. Например, для биткоин-адреса префикс равен 0 (0x00 в шестнадцатеричной системе счисления), для закрытого ключа - 128 (0x80 в шестнадцатеричной системе счисления). Соответственно, в кодировке Base58Check запись биткоин-адреса будет начинаться с цифры 1, а закрытого ключа формата WIF - с цифры 5. Список основных префиксов версий типов данных приводится в таблице:
| Категория данных | Префикс в шестнадцатеричной системе счисления | Результат кодирования с помощью Base58Check |
|---|---|---|
| Биткоин-адрес | 0x00 | 1 |
| Pay-to-Script-Hash адрес | 0x05 | 3 |
| Адрес для тестовой Биткоин сети | 0x6F | m или n |
| Приватный ключ WIF | 0x80 | 5, K или L |
| Зашифрованный приватный ключ | 0x0142 | 6P |
| Расширенный публичный ключ | 0x0488B21E | xpub |
Суммируя вышеизложенное, сформулируем алгоритм работы системы кодирования Base58Check:
- К кодируемым данным в соответствии с их типом добавляется специальный префикс (в начало числовой последовательности).
-
Вычисляется контрольная сумма путем двойного применения алгоритма хеширования к результату предыдущего этапа. Результатом хеширования является 32-х байтный дайджест, из которого мы выбираем только первые четыре байта. Именно эти 32 бита будут служить основанием для выявления ошибок, т.е., контрольной суммой. Формально это можно записать следующим образом:
контрольная сумма = первые четыре байта (SHA-256(SHA-256(префикс + данные))), где + означает операцию слияния.
- Затем контрольная сумма записывается в конец числовой последовательности.
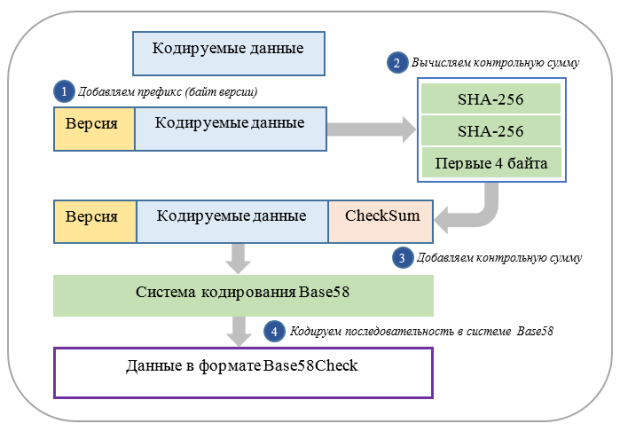
- Полученная последовательность (префикс + данные + контрольная сумма) кодируется с использованием системы Base58.
Данный процесс иллюстрируется схемой, изображенной на рисунке 14.
Большинство данных в сети Биткоин, с которыми работает пользователь, представлены в кодировке Base58Check. Такая форма записи удовлетворяет сразу трем немаловажным требованиям: компактность, удобство для восприятия и дополнительная защита от ошибок.
Пример формирования биткоин-адреса
Цель: Исследовать процесс получения биткоин-адреса на конкретном примере.
В качестве иллюстрации рассмотренных процедур приведем пример создания биткоин-адреса:
-
Начинаем с открытого ключа (65 байт, первый байт = 0x04, следующие 32 байта соответствуют координате X и заканчивается последовательность 32 байтами, соответствующими координате Y):
04678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb649f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f
- Применяем к открытому ключу хеш-функцию SHA-256:
261c1eb21fc4708c6acbe1cfc6d4565652e9e768b620782898936b93000a6c02
- Применяем к результату предыдущего шага хеш-функцию RIPEMD-160:
62e907b15cbf27d5425399ebf6f0fb50ebb88f18
- Добавляем байт версии в начало результата предыдущего шага (0x00 биткоин-адрес основной сети):
0062e907b15cbf27d5425399ebf6f0fb50ebb88f18
- Применяем к результату предыдущего шага хеш-функцию SHA-256:
9b90f16de7f0e580c07735dac15ffe23e2f8f8e103914e509aa91913ffdb9fb6
- Применяем к результату предыдущего шага хеш-функцию SHA-256 (для нахождения контрольной суммы):
c29b7d937e3049e279391e62fdf00c12def7444013ddf6215808d10e9f2d5996
- Находим контрольную сумму (первые 4 байта от дайджеста, полученного на предыдущем шаге):
c29b7d93
- Добавляем контрольную сумму в конец числовой последовательности (расширенный дайджест хеш-функции RIPEMD-160), полученной в пункте 4. Результатом является 25-байтный двоичный биткоин-адрес:
0062e907b15cbf27d5425399ebf6f0fb50ebb88f18c29b7d93
- Результат предыдущего пункта конвертируем в строку формата Base58. Получаем самый популярный формат записи биткоин-адреса (34 символа).
1A1zP1eP5QGefi2DMPTfTL5SLmv7DivfNa
Сжатые открытые ключи
Цель: Сформировать четкое понимание процесса и развить практические навыки получения сжатых открытых ключей в сети Биткоин.
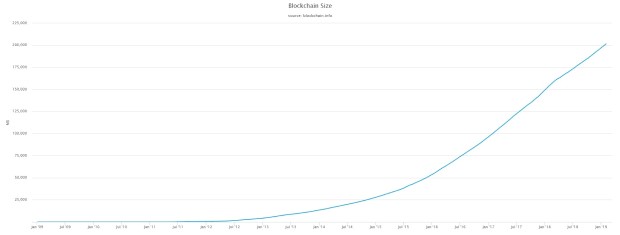
Оказывается, даже педантичным компьютерам и телекоммуникационным сетям, не путающимся в цифрах, не очень удобно работать с открытыми ключами в оригинальном виде. Правда, претензии у них несколько иного рода. Публичные ключи фигурируют в составе большинства транзакций. Это необходимо для проверки учетных данных владельца при совершении платежа. Каждый открытый ключ требует 520 битов памяти для хранения. Каждый день в сети Биткоин регистрируются десятки тысяч транзакций в день, существенно раздувая размеры блокчейна. Для распределенной системы, подразумевающей, что копия реестра должна храниться у каждого участника сети (пока мы не рассматриваем более простые вари анты с легкими кошельками) такая динамика становится очень накладной и грозит стать запредельной. Отметим, что на начало февраля 2019 года размер блокчейна платформы Биткоин превысил 236.68 GB. Вы сами можете оценить перспективы роста на основе графика динамики размера блокчейна сети Биткоин за 10 лет ее существования:
Сжатые открытые ключи были разработаны с целью уменьшения размера транзакций и сокращения размера блокчейна. Как мы уже знаем, открытый ключ — это точка на эллиптической кривой. Поскольку кривая является реализацией математической функции, точка на кривой представляет собой решение уравнения, а значит, если мы знаем x координату, то мы можем вычислить y координату. Для этого достаточно решить известное уравнение
y2 mod p = x3 + 7 (mod p)
Это соображение позволяет построить систему, в которой хранится только одна координата, входящая в открытый ключ. Экономия составляет ровно 256 бит, почти 50%. А вычислением недостающей координаты вполне может заняться программное обеспечение платформы Биткоин, например, же кошельки.
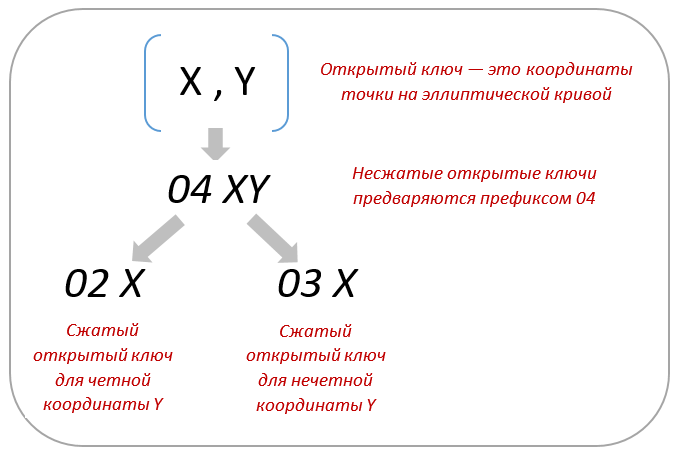
Чтобы не запутаться в таком многообразии ключей, разработчики снова прибегли к системе префиксов. Если несжатые открытые ключи предваряются префиксом 04, то сжатые начинаются с 02, или с 03. Выясним причину появления двух возможных префиксов. Проблема заключается в том, что, если точка лежит на эллиптической кривой, то для заданной Х координаты очевидно существуют два решения уравнения (в формуле у нас фигурирует y2 и эллиптическая кривая симметрична относительно оси Х). В данном случае можно воспользоваться следующим свойством функции, определенной над конечным полем: если для Х координаты существуют решения уравнения, то одна из точек будет иметь четную Y координату, а вторая — нечетную. Для первого случая был зарезервирован префикс 0x02 (в шестнадцатеричной системе счисления), а для второго - 0x03 (в шестнадцатеричной системе счисления).
Небольшая иллюстрация на рисунке 16 позволяет визуализировать этот процесс.
Приведем также пример в цифрах. Пусть у нас имеется открытый ключ, представленный двумя координатами (каждая представлена 256-битным числом или 64 шестнадцатеричными цифрами):
x = F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A y = 07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB
Запишем его в несжатом виде (520-битное число или 130 шестнадцатеричных цифр с префиксом 0x04):
K = 04F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB
А теперь представим его в сжатом виде (264-битное число или 66 шестнадцатеричных цифр с префиксом 0x03, указывающим на нечетность значения второй координаты):
K = 03F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
Это сжатый открытый ключ точно также соответствует исходному закрытому ключу и может быть из него получен. При этом выглядит он иначе. Более того, если мы сконвертируем этот сжатый открытый ключ в биткоин-адрес, используя двойное хеширование (RIPEMD-160(SHA-256(K))), то получим другой биткоин-адрес. Это может привести к путанице, так как означает, что от одного и того же приватного ключа может быть получен публичный ключ, выраженный в двух различных форматах (сжатом и несжатом), которым соответствуют два разных адреса Биткоин. Тем не менее, приватный ключ является единым для обоих адресов.
Несжатые открытые ключи постепенно вытесняются в платформе Биткоин. Современное клиентское программное обеспечение по умолчанию оперирует именно сжатыми открытыми ключами, что, безусловно благотворно сказывается на размерах транзаккций и, как следствие, блокчейна. Тем не менее, пока еще не все клиентское программное обеспечение поддерживает сжатые открытые ключи. С другой стороны, новые клиенты, поддерживающие прогрессивную схему сжатия открытых ключей, одновременно должны уметь работать с транзакциями, созданными в старой парадигме. Это особенно важно, когда приложение кошелька импортирует секретные ключи из другой программы, потому что новый кошелек должен просканировать блокчейн в поиске транзакций, соответствующих этим импортируемым ключам. В условиях неопределенности задачи поиска (Какие именно биткоин-адреса следует искать? На основе каких открытых ключей они были получены – сжатых или несжатых?) новое программное обеспечение кошельков позволяет пометить особым образом закрытые ключи, на основе которых были получены сжатые открытые ключи и, соответственно, сжатые биткоин-адреса.
Сжатые закрытые ключи
Цель: Сформировать четкое понимание процесса и развить практические навыки получения сжатых закрытых ключей в сети Биткоин.
На самом деле ни о каком сжатии в том смысле, который вкладывался в процесс сжатия открытых ключей, речь совершенно не идет. Более того, размер сжатого закрытого ключа окажется на один байт больше, чем размер обычного, несжатого, за счет дополнительного суффикса 0x01, добавленного с правого края числовой последовательности. Этот суффикс подчеркивает тот факт, что используется новая схема вычисления открытых ключей и для данного закрытого ключа могут формироваться только сжатые открытые ключи.
Особо отметим, что данные форматы ключей не взаимозаменяемы. В современных кошельках, которые используют сжатые открытые ключи, закрытые ключи будут экспортированы только сжатыми (с префиксом K или L). Если кошелек старого образца и не использует сжатые открытые ключи, закрытые ключи будут экспортированы в формате WIF (с префиксом 5). Актуальной остается задача просигнализировать импортирующему кошельку, что он должен просканировать блокчейн на предмет сжатых или несжатых публичных ключей и адресов.
Если программное обеспечение кошелька поддерживает сжатые публичные ключи, именно они будут использоваться во всех транзакциях. На их основе также вычисляются биткоин-адреса, которые, в свою очередь, используются в транзакциях. При экспорте приватных ключей из современного кошелька, поддерживающего сжатые публичные ключи, используется модифицированный Wallet Import Format с добавлением одного байта суффикса 0x01 к закрытому ключу. Такой закрытый ключ в кодировке Base58Check называется "сжатый WIF" и начинается с буквы К или L, а не с 5, как в случае с несжатыми ключами WIF формата из более старых кошельков. В таблице 3 приведены примеры записи одного и того же закрытого ключа в разных форматах.
| Формат | Закрытый ключ |
|---|---|
| Шестнадцатиричный | 1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD |
| WIF | 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn |
| Сжатый шестнадцатиричный | 1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD01 |
| Сжатый WIF | KxFC1jmwwCoACiCAWZ3eXa96mBM6tb3TYzGmf6YwgdGWZgawvrtJ |
Кошельки
Цель: Сформировать представление о различных типах кошельков, используемых в сети Биткоин.
Типы криптовалютных кошельков
Выбор кошелька для криптовалюты давно перестал быть вопросом исключительно безопасности или простоты. Использование разных кошельков для разных целей становится обычным делом, как и использование разных счетов при работе с фиатными деньгами. Разработчики программного обеспечения активно эксплуатируют эту концепцию и непрерывно предлагают новые программные средства, в том числе и вполне работоспособные. Описание этого вышедшего из берегов бурного потока разработок никак не укладывается в парадигму книги, поэтому информацию для выбора криптовалютного кошелька для собственных целей предлагаю почерпнуть в Интернете – благо ее там сейчас предостаточно. Нас же в первую очередь будут интересовать архитектурные аспекты их реализации.
В отличие от традиционных банковских счетов, работающих с фиатными деньгами, криптокошельки не хранят наличность в буквальном смысле. Они содержат открытые и секретные цифровые ключи, предоставляющие доступ к биткоин-адресам, и позволяют подписывать транзакции. При совершении платежных операций в блокчейне появляется запись о переходе прав на определенную сумму криптовалюты к новому владельцу, фактической передачи ценностей при этом не происходит.
По способу хранения наиболее критичной информации (конечно же речь идет о ключах) кошельки принято делить на "горячие" и "холодные". К первым относятся кошельки с постоянным доступом к интернету: онлайн-кошельки, мобильные приложения, программы для персональных компьютеров, имеющих постоянное подключение к сети Интернет. Безусловно, они очень удобны в использовании, обеспечивают синхронизацию блокчейна и готовы мгновенно обрабатывать транзакции. При этом они подвержены хакерским атакам и вирусам. И уж тем более не стоит серьезно относиться к кошелькам, предлагаемым криптовалютными биржами. Доверять секретные ключи посреднику - не самая лучшая стратегия.
В системах, реализующих принцип холодного хранения, критичные данные хранятся в оффлайн-режиме на физическом носителе, не имеющим прямого соединения с Интернетом. Разумеется, такой способ обеспечивают гораздо более высокую степень защиты криптовалютной наличности. При этом в плане проведения транзакций они не столь удобны. Другой угрозой является отличная от нуля вероятность поломки спец.техники или ее потери. Но здесь есть традиционный и достаточно простой способ защиты – своевременное создание резервных копий критичных данных. Холодный способ хранения реализуется в бумажных кошельках (имеются даже зашифрованные бумажные кошельки), системах с дополнительным физическим носителем и специальных аппаратных кошельках (например, Trezor, Keepkey или Ledger Nano S).
В заключение приведем достаточно простой вариант классификации криптовалютных кошельков, учитывающий в первую очередь технологию изготовления:
- Веб-кошельки (или онлайн кошельки).
Идеально подходят для новичков, не желающих самостоятельно администрировать собственное программное обеспечение, или обладателей "маломощной" вычислительной техники.
Популярные онлайн (браузерные) кошельки: Матби; Coinbase; Blockchain.info; Cryptopay; Xapo; Bitpay и др.
Достоинства:
- Отсутствует необходимость в скачивании, хранении и последующей синхронизации блокчейна (очень серьезно экономит время и место на постоянных носителях);
- Управлять Веб-кошельком можно с самых разных устройств. Единственное условие наличие свободного доступа к Интернету.
- Дополнительные сервисы и профессиональная поддержка.
Недостатки:
- Низкий уровень защиты (секретный ключ хранится на стороне, у какого-то дяди, пусть даже и очень авторитетного).
- Мобильные кошельки (устанавливаются на смартфоны и т.п.).
Мобильные клиенты позволяют совершать платежи по схеме scan-and-pay. Нет необходимости прокатывать карту, набирать PIN-код или вносить данные вручную. Единственное, что нужно для приема платежа, это открыть QR-код в своем мобильном кошельке и показать его контрагенту, чтобы он просканировал код своим мобильным телефоном, или просто поднести телефоны друг к другу (если они поддерживают технологию NFC). Мобильные кошельки, чтобы не скачивать весь блокчейн, хранят только его облегченную версию. А при транзакциях обращаются к доверенным нодам. Делается это, чтобы сэкономить столь значимые для телефона ресурсы как память и трафик.
Популярные кошельки для мобильных устройств: Blockchain Mobile; Bitcoin Wallet; Electrum; Mycelium; Coin Pocket; Xapo и др.
Очевидное достоинство - удобство использования при оплате и постоянный доступ к кошельку.
В качестве недостатка отметим высокую вероятность кражи самого телефона или потери. Дискредитации ключей в этом случае может помешать высокая степень безопасности (двухуровневая аутентификация, смс-оповещения), которую обеспечивают мобильные криптовалютные кошельки.
-
Локальные кошельки (установленные на персональный компьютер или ноутбук).
Подразделятся на два вида. "Толстые" или "тяжелые" – такие кошельки загружают на компьютер весь блокчейн, возводя пользователя в ранг полноценного участника сети Биткоин и занимая при этом большой объем памяти на постоянном носителе (на начало февраля 2019 года – уже более 236 GB). В отличие от тяжелых криптокошельков "тонкие" или "легкие" не скачивают весь блокчейн на персональный компьютер, а обращаются к нему через API сторонних агрегаторов. Занимают значительно меньше места по сравнению с толстыми, несколько быстрее проводят транзакции, но из-за обращений к стороннему ресурсу уступают толстым в безопасности. Хотя приватные ключи в обоих случаях хранятся у пользователя.
Популярные локальные кошельки: Bitcoin Core; Electrum; Jaxx; Exodus и др.
Обеспечивают достаточно высокий уровень надежности кошелька и защищенности средств. Но при этом могут занимать очень много места на жестком диске и долго синхронизируются с блокчейном.
-
Аппаратные кошельки (в виде отдельного устройства).
При инициализации таких устройств вводится код, ограничивающий доступ к аппаратному кошельку в случае его потери или кражи. Взломать данное устройство невозможно. Все транзакции совершаются в защищенной среде прибора. Даже, если подключить аппаратный кошелек к взломанному персональному компьютеру, злоумышленникам не удастся получить контроль над кошельком.
Единственным недостатком является довольно высокая цена (порядка $100).
- Бумажные кошельки.
Это обычный листок бумаги, на которой распечатаны приватные и открытые ключи в виде QR-кода. Для практического использования этих ключей их следует отсканировать. Безусловно, в плане удобства уступают аппаратным кошелькам, но тем не менее обеспечивают сравнимый с ними высокий уровень безопасности.
Детерминированные и недетерминированные (случайные) кошельки
Рассмотрим кошелек, с точки зрения организации процедуры хранения закрытых ключей. Недетерминированные кошельки реализуются в форме структурированных файлов или простейших баз данных. В ответ на желание владельца независимым (случайным) образом программным обеспечением кошелька генерируется очередной закрытый ключ, помещаемый в хранилище. Например, клиент Bitcoin Core в момент инициализации генерирует сразу 100 закрытых ключей. Разумеется, в случае необходимости формируются дополнительные ключи. Такая стратегия создает препятствия для операций резервного копирования, импорта/экспорта. Необходимо хранить довольно большой набор несвязанных случайных данных. Массовый выпуск приватных ключей даже не приводит к повышению конфиденциальности, поскольку появляются основания для отслеживания связи между различными адресами и транзакциями. Поэтому разработчики, сохраняя в своих клиентах возможность использования недетерминированного механизма, настоятельно рекомендуют использовать детерминированный способ генерации ключей.
В этом случае каждый новый закрытый ключ формируется путем применения односторонней хеш-функции к значению последнего, ранее сгенерированного закрытого ключа. В результате образуется цепочка секретных данных (вполне в духе технологии блокчейн). Для того чтобы воссоздать всю последовательность, достаточно знать только первый ключ (называемый зерном или мастер-ключом).
На практике применяются довольно много различных методов генерации ключей и структур кошелька, использующих эту идею. Мы остановимся только на двух технических решениях.
Детерминированные кошельки (с зерном)
Что именно должно представлять собой зерно? Зерно — это случайное число, которое в сочетании с другими параметрами, такими как номер индекса или "код цепи" позволяет получить всю цепочку приватных ключей. При такой стратегии для восстановления всех закрытых ключей достаточно знать только зерно. Следовательно, достаточно единожды сформировать его резервную копию в момент создания, а не дублировать данные каждый раз, когда генерируется новый ключ, как это имело место в случае недетерминированного кошелька. Аналогичным образом упрощаются операции импорта/экспорта. Достаточно оперировать одним зерном, что кардинально снижает затраты и риски в процессах миграции ключей между различными реализациями кошельков.
Мнемонические кодовые слова
Компьютер замечательно запоминает числа, а вот человек лучше оперирует словами, еще лучше, если эти слова наделены смыслом. Именно на этом простом факте основан один из подходов к формированию зерна. Мнемонические коды — это некоторая строка, состоящая из английских слов, которая уникальным образом представляет (по сути - кодируют) случайное число, которое может быть использовано в качестве зерна для детерминированного кошелька. Этой строки вполне достаточно для того, чтобы заново создать зерно, а, используя его, воссоздать кошелек полностью, включая все производные ключи.
Работает это следующим образом. Приложение детерминированного кошелька с мнемоническим кодом в момент инициализации представит пользователю последовательность слов (числом от 12 до 24). Эта строка является резервной копией кошелька и может быть использована для восстановления и повторного создания всех ключей в таком же или любом другом совместимом клиенте.
Теоретически мнемоническую фразу можно придумать самому, но это небезопасно, так как человек плохо справляется со случайной генерацией. Лучший способ обезопасить свой кошелек – взять мнемоническую фразу, созданную с помощью специального генератора фраз.
Опишем процедуру создания мнемонического кода и зерна:
- Создаем случайную числовую последовательность (энтропию) (от 128 до 256 бит).
- Применяем к числу, полученному на первом шаге, хеш-функцию SHA-256. Выбираем первые несколько битов из вычисленного дайджеста. Будем называть их контрольной суммой.
- Добавляем контрольную сумму в конец случайной последовательности.
- Разделяем результат предыдущего шага на части длиной в 11 бит, и используем их в качестве индекса по словарю из 2048 заранее определенных слов.
- Выбираем по индексам от 12 до 24 слов из словаря. Полученная фраза и будет представлять мнемонический код.
Англоязычный список слов для стандарта BIP39 (Mnemonic code for generating deterministic keys) содержит 2048 слов. Если фраза состоит из 12 слов, тогда число возможных комбинаций составляет 2048 в 12-й степени, или 2 в 132-й степени, то есть фраза обеспечит 132 бита безопасности. Для фразы из 24 слов энтропия возрастет до 256 бит.
Итак, мнемонический код представляет собой последовательность от 128 до 256 бит, которая впоследствии используется для получения более длинного (512 бит) зерна путем применения функции удлинения ключа PBKDF2 (Password-Based Key Derivation Function - стандарт формирования ключа на основе пароля). Полученное зерно готово для создания детерминированного кошелька и соответствующих ключей.
В таблице 4 представлены примеры некоторых мнемонических кодов и зерен, которые они производят
| Энтропия на входе | Мнемонический код | Зерно (512 бит) |
|---|---|---|
| 0c1e24e5917779d297e14d45f14e1a1a (128 бит) | army van defense carry jealous true garbage claim echo media make crunch (12 слов) | 3338a6d2ee71c7f28eb5b882159634cd46a8984 63e9d2d0980f8e80dfbba5b0fa0291e5fb888a599 b44b93187be6ee3ab5fd3ead7dd646341b2cdb8d 08d13bf7 |
| 2041546864449caff939d32d574753fe6 84d3c947c3346713dd8423e74abcf8c (256 бит) | cake apple borrow silk endorse fitness top denial coil riot stay wolf luggage oxygen faint major edit measure invite love trap field dilemma oblige (24 слова) | 3972e432e99040f75ebe13a660110c3e29d131a2c 808c7ee5f1631d0a977fcf473bee22fce540af281bf 7cdeade0dd2c1c795bd02f1e4049e205a0158906 c343 |
Иерархические детерминированные кошельки
Наиболее эффективной формой детерминированных кошельков является иерархический детерминистический кошелек или HD-кошелек, описанный в стандарте BIP0032 (Hierarchical Deterministic Wallets). Иерархические детерминированные кошельки содержат ключи в виде древовидной структуры, так что из родительского ключа можно вывести последовательность производных ключей, от каждого из которых, в свою очередь, также получается последовательность производных ключей и так далее без ограничения глубины вложений. HD-кошельки предлагают два основных преимущества по сравнению с недетерминированными. Во-первых, структура дерева может быть послужить в целях дополнительной организации, например, когда одна ветвь ключей используется для получения входящих платежей, а другая ветвь определена для получения сдачи для исходящих платежей. Ветвление ключей также может быть использовано в корпоративной среде для различных отделов, филиалов, конкретных функций, или категорий бухгалтерского учета.
Следующее преимущество HD-кошельков состоит в том, что их пользователи могут создавать последовательности открытых ключей, не имея доступа к соответствующим закрытым ключам. Это обстоятельство позволяет использовать HD-кошельки на небезопасных серверах или в режиме только приема средств с выдачей нового публичного ключа для каждой новой транзакции. Открытые ключи не должны быть предварительно загружены или получены заранее и сервер не содержит закрытые ключи, которые могут использоваться для доступа к средствам.
Шифрованные закрытые ключи
Как это часто бывает в практике обеспечения информационной безопасности, два ее важнейших аспекта – доступность и конфиденциальность - в отношении хранения закрытых ключей предъявляют противоречивые требования. Шифрование могло бы кардинально повысить секретность закрытых ключей. Однако, безсистемное применение этого мощного инструмента существенно осложняет выполнение многих необходимых в платежных системах операций, таких как создание резервных копий, миграция ключей из одного кошелька в другой, обновление программного обеспечения клиентов и т.д.
Эти соображения побудили IT-сообщество, участвующее в развитии и совершенствовании платформы Биткоин, разработать общий стандарт шифрования закрытых ключей - Предложения по улучшению Биткоина BIP0038. Предлагаемый универсальный алгоритм одновременно является простым, удобным и эффективным. Для шифрования закрытых ключей используется кодовая фраза, результат кодируется с помощью Base58Check. Таким образом обеспечивается надежность хранения секретной информации на резервных носителях, адекватность алгоритмов передачи ключей между кошельками, не столь критичными становятся ситуации, в которых ключи могут быть обнаружены. Стандартом для шифрования был выбран Advanced Encryption Standard (AES) - симметричный алгоритм блочного шифрования, принятый в National Institute of Standards and Technology (NIST).
Криптосистема, рекомендованная BIP0038, принимает на входе приватный ключ, обычно кодируемый в WIF-формате (Base58Check-строка с префиксом 5). Параллельно с этим вводится ключевая фраза - длинный пароль, обычно состоящий из нескольких слов или представляющий собой последовательность алфавитно-цифровых символов. Результатом работы криптосистемы является приватный ключ в кодировке Base58Check с префиксом 6P. Всегда, когда Вам попадается закрытый ключ, начинающийся с 6P, это означает, что он зашифрован и должен быть преобразован обратно в формат WIF (префикс 5). Для дешифрования потребуется упомянутая выше секретная фраза. Программное обеспечение большинства современных кошельков поддерживает стандарт BIP0038.
С зашифрованными закрытыми ключами работают также сторонние приложения, например, https://www.bitaddress.org
Очень часто приведенная технология шифрования ключей используется в бумажных кошельках. Владельцу достаточно выбрать сильную секретную фразу, чтобы обеспечить бумажному кошельку с зашифрованными (по схеме BIP0038) закрытыми ключами обеспечивает чрезвычайно высокий уровень безопасности и является весьма эффективным способом холодного хранения.
| Закрытый ключ (WIF) | 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2Jpbnk |
| Секретная фраза: | MyTestPassphrase |
| Зашифрованный закрытый ключ | 6PRTHL6mWa48xSopbU1cKrVjpKbBZxcLRRCdctLJ3z5yxE87MobKoXdTsJ |
Pay-to-Script Hash (P2SH) адреса и мульти-подписи
Цель: Сформировать начальное представление о P2SH-транзакциях и мультиподписных платежах, акцентируясь на особенностях, представляющих их биткоин-адресах.
Pay-to-Script Hash адреса
Ранее рассматривалась стандартная процедура формирования адреса по схеме закрытый ключ -> открытый ключ -> биткоин-адрес. Такие адреса начинаются с цифры "1". Каждый участник сети Биткоин может оправить средства на такой адрес. А вот для того чтобы их потратить, необходимо обладать соответствующим закрытым ключом. Тут, как говорится, без вариантов. Способ P2PKH (Pay-to-Public-Key-Hash) являются основной формой реализации транзакций в сети Биткоин. Такие транзакции "блокируют биткоины" на своих выходах. Впоследствии средства могут быть разблокированы и тут же снова заблокированы последующими транзакциями. Подобным образом биткоины легко мигрируют с одного адреса на другой. Транзакции, отправляющие средства на биткоин-адрес, содержат скрипты P2PKH, разрешающиеся с помощью открытого ключа и электронной подписи, созданной на основе соответствующего закрытого ключа. В случае стандартной транзакции скрипт включается в ее выход.
Большинство нестандартных платежей, например, мульти-подписи или проверка условия, что определенный выход транзакции не может быть потрачен до определенного момента времени в будущем (CheckLockTimeVerify), используют более сложные схемы, с общим названием P2SH (Pay to Script Hash - "оплата по хешу скрипта"). Такие биткоин- адреса, начинаются с цифры "3".
P2SH транзакции были введены Гэвином Андресеном в январе 2012 года. Цель нововведения по словам Андресена состояла в том, чтобы "перенести ответственность за предоставление условий по выкупу транзакции с отправителя средств на того, кто данные средства тратит".
При использовании способа оплаты P2SH биткоины также блокируются в скрипте. Однако сам скрипт не включается в выход транзакции. Вместо этого сценарий разблокировки хешируется, а результат этот операции записывается в выход транзакции. Как и принято в криптографии, полученный дайджест нельзя использовать для восстановления оригинального скрипта. Для хеширования pay-to-script используется тот же алгоритм, который используется при создании биткоин-адреса (двойное хеширование), только применяется он к сценарию, а не к открытому ключу. Полученный дайджест кодируется при помощи Base58Check с версией префикса 0x05, что дает закодированный адрес, начинающийся с 0x03.
Для разблокировки выхода P2SH в последующей транзакции, недостаточно выполнения сформулированных в скрипте условий. Нодам в сети Биткоин вообще доступен только хеш скрипта, а не сам сценарий. Поэтому, никакая нода не может подтвердить выполнение предусмотренных в скрипте условий. Кроме той, которой известен весь сценарий блокировки. Именно поэтому следующая транзакция, расходующая биткоины, должна включать в себя скрипт целиком, а также сформулированные в нем условия (блокировка (скрипт) + ключ (условия) для разблокировки средств).
Иначе говоря, начиная с 2012 года при использовании решения P2SH только новый держатель средств знает, как можно их потратить, остальные участники сети не знают условий блокировки средств (скриптов), вплоть до их разблокирования - траты. Достигается это путем включения в блокчейн только хеш-дайджестов исходных скриптов. Именно хеши регулируют права собственности на наличность. В момент траты владелец предоставляет исходный текст скрипта и ключ для расшифровки хеш-дайджеста одновременно. После этого каждый пользователь сети Биткоин может проверить истинность скрипта и выполнение условий траты на основе начального хеша.
Как же будет организована трата средств, заблокированных P2SH-транзакцией? В разблокирующей транзакции приводится оригинальный скрипт (скрипт погашения). Затем майнеры, хешируя фактический скрипт, смогут подтвердить, что представленный скрипт соответствует хешу, включенному в заблокированный выход. Таким образом транзакция может быть подтверждена и включена в блок, а затем и в блокчейн.
Способы оплаты P2SH чаще всего представляют сценарии мульти-подписи, но они также могут представлять сценарии, реализующие другие типы транзакций.
У P2SH-транзакций существует определенный набор преимуществ перед аналогами:
- Отправитель может финансировать любой произвольный сценарий погашения, не зная, каковы эти условия расходов. Это имеет смысл, если отправителю во многом все равно, как будут потрачены эти средства в будущем – это вопрос для получателя, которому небезразличны условия дальнейшего расходования средств. В случае транзакций с мультиподписью, отправитель может отправить средства, не зная необходимые открытые ключи, принадлежащие получателю, адреса получателя, которые раскрываются только тогда, когда получатель тратит средства. Подобный вид сделки повышает безопасность получателя.
- Отправитель может использовать короткий 34-символьный адрес, подобный указанному выше, вместо длинного и громоздкого адреса, содержащего сведения о сценарии полного погашения. Это позволяет получателю разместить короткий адрес на платежной странице или в сообщении, что снижает вероятность человеческих ошибок в транскрипции.
- Такой способ снижает операционные сборы для отправителя средств. Комиссии за транзакцию пропорциональны размеру транзакции, а дайджест фиксированной длины позволяет отправителю перечислять средства на любой произвольный скрипт погашения, не беспокоясь о выплате более высоких сборов. Это ответственность получателя, который создает скрипт погашения, чтобы определить, насколько велика будет их транзакция расходов и сколько это будет стоить. На данный момент это не является большой проблемой в связи с тем, что транзакционные издержки довольно малы. Однако они могут быть более важными в будущем, поскольку вознаграждение за блок в сети Биткоин постоянно уменьшается.
Обычно реализация функции P2SH является мульти-подписью адреса скрипта. В данном сценарии необходимо, чтобы выход транзакции разблокировался более чем одной электронной подписью, чтобы доказать право собственности и, следовательно, потратить средства.
Мульти-подписи
В настоящее время наиболее распространенной реализация функции P2SH — это сценарий мульти-подписного адреса. Как следует из названия, основной сценарий требует более одной подписи для доказательства права собственности и, следовательно, возможности распоряжения средствами.
Таким образом, мульти-подпись М-из-N, реализованная в сети Биткоин, означает, что для разблокирования выхода транзакции достаточно получить M подписей (это число также называют "порогом") из N возможных. При этом, М ? N.
К такому биткоин-адресу привязано сразу несколько пар ECDSA ключей. Каждая пара состоит из закрытого и открытого ключей. Схемы комбинаций, согласно которым можно использовать эти ключи, могут быть различными. Более того, можно установить условия, при которых нужно будет предоставить несколько подписей, чтобы потратить средства, заблокированные в выходе транзакции.
Существуют различные комбинации ключей при использовании мульти-подписи. Самыми популярными вариантами являются 2-из-2, 2-из-3, а также 3-из-3. Максимально возможный вариант — 15-из-15.
Технические аспекты реализации мульти-подписи рассмотрим в разделе, посвященном транзакциям.
Краткие итоги
Право владения любыми цифровыми активами устанавливается через криптографические ключи, биткоин-адреса и электронные подписи. Закрытые криптографические ключи не перемещаются по сети. Они генерируются и хранятся пользователями в специализированном клиенте (кошельке). Цифровые ключи в кошельке абсолютно независимы от протокола Биткоин. Благодаря такой стратегии управления ключами становятся возможными многие важнейшие свойства сети Биткоин, включая децентрализованные консенсус и контроль, подтверждение владения и модель безопасности, основанную на математическом (криптографическом) доказательстве.
В большинстве случаев биткоин-адрес формируется на основе публичного ключа. Однако протоколом Биткоин разрешаются адреса, реализуемые по иным схемам.
В сети Биткоин для создания криптопары, контролирующей доступ к счету, используется умножение на эллиптических кривых. Согласно протоколу Биткоин закрытый ключ (число длиной в 256 бит) генерируется случайным образом, открытый ключ (два 256-битных числа + 8 бит префикса типа) создается путем криптографического преобразования закрытого ключа с использованием алгоритма эллиптической криптографии secp256k1 – частного случая алгоритма ECDSA. Биткоин-адрес (число длиной в 200 бит) – результат последовательного двукратного вычисления хеш-функций (сначала SHA-256, а затем RIPEMD-160) публичного ключа и добавления к результату префикса типа (1 байт) и контрольной суммы (4 байта).
Для записи биткоин-адреса используется кодировка Base58Check, мощность алфавита которой составляет 58 символов.
Использование сжатых открытых ключей позволяет существенно сократить нагрузку на блокчейн за счет уменьшения размера транзакции.
Сжатые открытые ключи лишь подчеркивают факт использования программным обеспечением новой схемы вычисления открытых ключей исключительно в сжатом виде.
По способу хранения ключей кошельки принято делить на "горячие" и "холодные". Холодный способ хранения реализуется в бумажных кошельках (имеются даже зашифрованные бумажные кошельки), системах с дополнительным физическим носителем и специальных аппаратных кошельках (например, Trezor, Keepkey или Ledger Nano S).
Большинство нестандартных платежей, например, мульти-подписи или проверка условия, что определенный выход транзакции не может быть потрачен до определенного момента времени в будущем (CheckLockTimeVerify), используют схемы с общим названием P2SH. Такие биткоин- адреса, начинаются с цифры "3".