Нейрофизиологический и формально-логический базис нейроподобных вычислений
Если нейроподобный теоретико-групповой компилятор предназначен для синтеза нейро-ЭВМ, то следует учитывать, что стратегия адаптации (много)пороговых моделей формальных нейронов "дочерней" и "материнской" нейро-ЭВМ отличаются критериями эффективности, что не отражено в классической схеме (много)порогового элемента (рис. 4.30). В реальности адаптивные возможности составляющих элементов расходуются на практически несовместные цели:
- максимальную устойчивость реализации заданной логической функции в "дочерней" нейро-ЭВМ;
- минимальную избыточность управления "материнской" нейро-ЭВМ, что приводит к двум стратегиям и двум схемам управления вектором порогов.
Для достижения максимально устойчивой реализации заданной булевой функции 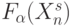 необходимо, чтобы вектор порогов смещался по скалярной оси, компенсируя паразитные флуктуации
необходимо, чтобы вектор порогов смещался по скалярной оси, компенсируя паразитные флуктуации 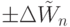 весового вектора
весового вектора  . Для этого достаточно (рис. 4.31) компоненты вектора порогов вычислять непрерывно с помощью оператора линейной свертки, но для фиксированного множества значений входного вектора
. Для этого достаточно (рис. 4.31) компоненты вектора порогов вычислять непрерывно с помощью оператора линейной свертки, но для фиксированного множества значений входного вектора 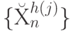 , определяющего левые и правые границы интервалов "эквизнач-ности" заданной булевой функции на скалярной оси
, определяющего левые и правые границы интервалов "эквизнач-ности" заданной булевой функции на скалярной оси 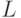 .
.
Поэтому, если формальный нейрон ориентирован на использование в "дочерней" нейро-ЭВМ, необходимо фиксировать подмножество значений входного вектора, по отношению к которому и определяется положение компонент вектора порогов. В этом случае правила выбора компонент вектора порогов для настройки (много)пороговой модели на реализацию, например, образующей булевой функции 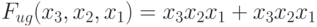 имеют вид
имеют вид  ;
;  ;
; 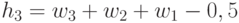 и
и 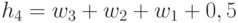 , система решающих пороговых правил имеет вид
, система решающих пороговых правил имеет вид 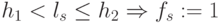 и
и 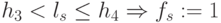 . В результате вариации весового вектора (заштрихованные клетки
табл. 4.8) приводят к тому, что система решающих правил
. В результате вариации весового вектора (заштрихованные клетки
табл. 4.8) приводят к тому, что система решающих правил
"отслеживает" положение одних и тех же (по индексу  ) значений
) значений 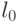 и
и 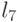 на упорядоченном множестве значений свертки
на упорядоченном множестве значений свертки  , то есть
, то есть 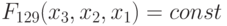 при всех вариациях весового вектора.
при всех вариациях весового вектора.
Для достижения минимальной избыточности управления "материнской" нейро-ЭВМ необходимо минимизировать количество образующих булевых функций, а вектор порогов минимальной размерности для каждой образующей определить с помощью системы решающих правил, указывающих только ранги значений свертки, между которыми необходимо размещать значения компонент вектора порогов. Поэтому если формальный нейрон ориентирован на использование в "материнской" нейро-ЭВМ, то для каждой образующей булевой функции необходимо зафиксировать не сами значения компонент вектора порогов, а только места их расположения (по индексу  ) на упорядоченном множестве значений свертки
) на упорядоченном множестве значений свертки  (рис. 4.32).
(рис. 4.32).
В частности, для настройки (много)пороговой модели на реализацию той же образующей булевой функции 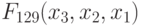 и сопряженного с ней класса необходимо, чтобы значение одного порога было больше минимального значения
и сопряженного с ней класса необходимо, чтобы значение одного порога было больше минимального значения  , а другого - меньше максимального значения
, а другого - меньше максимального значения  . В результате такой ранговой "фиксации" вектора порогов (заштрихованные клетки
табл. 4.9) вариации знаков весового вектора приводят к настройке (много)пороговой модели на реализацию еще трех булевых функций:
. В результате такой ранговой "фиксации" вектора порогов (заштрихованные клетки
табл. 4.9) вариации знаков весового вектора приводят к настройке (много)пороговой модели на реализацию еще трех булевых функций: 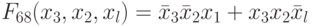 ,
, 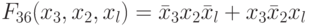 и
и 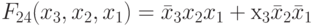 , с двукратной избыточностью управления, так как при фиксированном векторе порогов только половина вариаций знака компонент весового вектора порождает дополнительные булевы функции.
, с двукратной избыточностью управления, так как при фиксированном векторе порогов только половина вариаций знака компонент весового вектора порождает дополнительные булевы функции.
На основе приведенных данных можно заключить:
- Теоретико-групповая модель формального нейрона кардинальным образом снижает размерность задачи синтеза нейро-ЭВМ, сведя ее к задаче целочисленной оптимизации, которая проводится:
- на конечном множестве подстановок значений свертки входного сигнала, мощность которого в случае
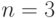 равна
равна 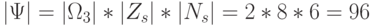 , а в случае
, а в случае 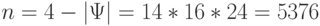 ;
; - на конечном множестве образующих (всего 13 для
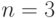 ) и отвечающим им классам смежных булевых функций, мощность которых в рамках одной первичной спецификации:
) и отвечающим им классам смежных булевых функций, мощность которых в рамках одной первичной спецификации:- для
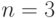 не превышает 24,
не превышает 24, - для
 даже при минимальном количестве порогов существенно зависит от системы решающих пороговых правил, используемых при реализации смежных классов по группе переименования переменных.
даже при минимальном количестве порогов существенно зависит от системы решающих пороговых правил, используемых при реализации смежных классов по группе переименования переменных.
- для
- на конечном множестве подстановок значений свертки входного сигнала, мощность которого в случае
- Согласно теореме Кэли [103] всякая конечная группа изоморфна некоторой группе подстановок. Это говорит о возможности использования нейротрансляторов для прямого отображения функций пользователя на уровень квантовых процессов, фундаментальные свойства которых описываются всевозможными группами симметрий.
- Формальные нейроны "дочерней" и "материнской" нейро-ЭВМ отличаются стратегией адаптации вектора порогов, которая в первом случае превращает формальный нейрон в классическую следящую систему, а во втором случае требует достаточно сложной схемы ранговой фильтрации значений свертки полного множества значений входных векторов
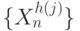 .
.
Системотехнические выводы по лекции 4
- Современные нейрохимические модели реальных нейронов требуют учета внутренних (метаболических) процессов, что не могло быть отражено в электрофизиологической модели Ходжкина - Хаксли, которая и была положена в основу ставших уже традиционными моделей формальных нейронов.
- Теория конвергентного замыкания условного рефлекса П.К. Анохина указывает на существование реальных "нейрокомпиляторов" с уровня межнейрональных взаимодействий на уровень метаболических процессов, и наоборот. В результате можно предположить: в реальной нервной системе "задание пользователя" доводится или, по крайней мере, может быть доведено до молекулярно-биологических взаимодействий, соподчиненных законам квантовой механики. Поэтому для преодоления трудностей декогерентизации квантовых систем осмысленным является поиск методов и средств прямого отображения заданий пользователя на физико-химический уровень работы "элементной базы", что требует высокодинамичного синтеза нанометровых и супрамолекулярных вычислительных структур с ограниченным "временем жизни".
- Теоретико-групповая модель формального нейрона позволяет решать задачи оптимального синтеза нейро-ЭВМ на конечном множестве целочисленных вариаций весового и порогового векторов, что и создает предпосылки для прямого отображения задач пользователя нейро-ЭВМ на квантовые процессы наноэлектронных систем, фундаментальные свойства которых определяются и описываются группами симметрий. При этом сохраняется традиционная схема кремниевой компиляции с использованием библиотек стандартных элементов, которая и ограничивает совокупность используемых теоретико-групповых преобразований, отвечающих физико-химическому уровню описания работы реализуемой нанометровой или супрамолекулярной элементной базы.
- Переход к теоретико-групповым нейрокомпиляторам открывает новые возможности инструктированного синтеза нанометровых или супрамолекулярных вычислительных структур "нечисленными" методами и средствами, основанными на проверке отношения "больше-меньше", для чего требуются тривиальные "рычажные весы" уровня квантовых взаимодействий.
- В реальных нейронах и нейронных ансамблях используется комплекс взаимно обусловленных структурно-параметрических методов хранения и преобразования информации, в рамках которого отстоящая на значительном интервале времени предыстория фиксируется с помощью структурных методов, а оперативное преобразование информации осуществляется параметрическими методами.
- По своему предназначению и используемым методам проектная технология прототипирования только воспроизводит апробированные природой принципы и методы системогенеза, создающие для новорожденных необходимые предпосылки их выживания еще на стадии их эмбрионального развития.
- Эволюционный опыт развития организмов говорит о том, что только иерархическим полимодальным комплексом мер можно обеспечить жизнедеятельность "сложных систем", синтезируемых "ненадежными" методами и средствами из "ненадежных" компонент с малым "временем жизни", что характерно для нанометровых и супрамоле-кулярных вычислителей. При этом в увеличение "сложности" системы решающий вклад вносит не "объект", а "средство" поддержания его жизнеспособности в постоянно изменяющемся комплексе внешних условий.



