Теория вычислений и машины Тьюринга
3.3. Машины Тьюринга и перечислимые множества
В математике кроме вычислительных алгоритмов, описывающих последовательности преобразований конструктивных объектов, существуют еще и процедуры перечисления таких объектов. Традиционно к таким процедурам относят перечисление простых чисел до некоторой заранее заданной границы. (К простым относят те числа, которые делятся только сами на себя и на единицу.) При этом считается известной процедура выделения простых чисел из натурального ряда (тест на делимость по отношению ко всем предшественникам) и занесения их в список в порядке возрастания, а временные и прочие трудности реализации перечислительной процедуры в расчет не принимаются. В результате все множество простых чисел считается перечислимым, а метод выделения и записи простых чисел называется перечислительной процедурой.
Приведенных соображений достаточно для введения интуитивно понимаемого определения 3.2 [50]: множество  -членных последовательностей слов над некоторым алфавитом называется перечислимым, если существует общая процедура, с помощью которой можно систематическим образом получить все элементы
-членных последовательностей слов над некоторым алфавитом называется перечислимым, если существует общая процедура, с помощью которой можно систематическим образом получить все элементы  .
.
В частности, для перечисления множества слов над некоторым алфавитом  подходят две процедуры со следующими предписаниями [50]:
подходят две процедуры со следующими предписаниями [50]:
- Сначала пишется пустое слово. Если выписанное слово
 имеет длину
имеет длину  , то далее пишется слово длины
, то далее пишется слово длины  над
над  , которое следует лексикографически непосредственно за
, которое следует лексикографически непосредственно за  , и при условии, что
, и при условии, что  не лексикографически последнее слово длины
не лексикографически последнее слово длины  над
над  . В противном случае пишут лексикографически первое слово длины
. В противном случае пишут лексикографически первое слово длины 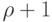 над
над  .
. - Сначала пишется пустое слово. Далее пишется слово, полученное из какого-то уже выписанного слова, добавлением одной буквы из
 .
.
Очевидно, что первое предписание однозначно задает последовательность слов над  , в то время как во втором предписании допускается произвол в выборе как "уже выписанного слова", так и дописываемой буквы. В первом случае можно установить соответствие между вычислимостью и перечислимостью по Тьюрингу, в то время как во втором случае нарушается требование 4 для вычислимых по Тьюрингу алгоритмов, что вынуждает говорить о перечислимости через так называемые исчисления или системы правил вывода [50]. В результате в неоднозначных перечислительных процедурах на передний план выходят не проблемы перечисления элементов некоторого множества, а креативный (познавательный) аспект этой процедуры и порождаемых ею креативных множеств.
, в то время как во втором предписании допускается произвол в выборе как "уже выписанного слова", так и дописываемой буквы. В первом случае можно установить соответствие между вычислимостью и перечислимостью по Тьюрингу, в то время как во втором случае нарушается требование 4 для вычислимых по Тьюрингу алгоритмов, что вынуждает говорить о перечислимости через так называемые исчисления или системы правил вывода [50]. В результате в неоднозначных перечислительных процедурах на передний план выходят не проблемы перечисления элементов некоторого множества, а креативный (познавательный) аспект этой процедуры и порождаемых ею креативных множеств.
Отсюда, получить точное определение перечислимости по Тьюрингу можно только для тех процедур, которые удовлетворяют не только требованию однозначности, но и всей совокупности требований 1-8, предъявляемых к вычислимым по Тьюрингу алгоритмам. При таких условиях тезис Черча распространяется и на перечислительные процедуры, что позволяет говорить об адекватном уточнении интуитивных представлений о перечислимости с помощью понятия перечислимости по Тьюрингу. Существенно, что ограничения 1-8 не только не выхолащивают, но и практически не ограничивают класс перечислимых множеств и процедур перечисления их элементов.
Покажем, что понятие вычислимости можно свести к понятию перечислимости, и наоборот, что и позволяет формализовать перечислимость с помощью уже имеющегося понятия вычислимости по Тьюрингу.
Сведем понятие вычислимости к понятию перечислимости, используя график функции  , который представляет собой множество
, который представляет собой множество 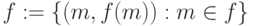 . Справедлива теорема [50]: Пусть
. Справедлива теорема [50]: Пусть  и
и  есть некоторая функция из
есть некоторая функция из 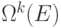 в
в 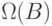 . Функция
. Функция  вычислима в том и только в том случае, когда множество
вычислима в том и только в том случае, когда множество 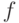 перечислимо. Доказательство прямого утверждения данной теоремы исходит из того, что если
перечислимо. Доказательство прямого утверждения данной теоремы исходит из того, что если  вычислима, то для нее существует вычислительная процедура
вычислима, то для нее существует вычислительная процедура 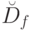 Всегда можно упорядочить лексикографически и пронумеровать числами натурального ряда элементы множества
Всегда можно упорядочить лексикографически и пронумеровать числами натурального ряда элементы множества 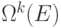 . Тогда элементы множества
. Тогда элементы множества 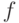 можно также пронумеровать числами натурального ряда, отвечающими числу шагов в процедуре
можно также пронумеровать числами натурального ряда, отвечающими числу шагов в процедуре 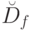 . Доказательство обратного утверждения строится на том, что процедуру
. Доказательство обратного утверждения строится на том, что процедуру 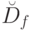 , вычисляющую
, вычисляющую  , всегда можно остановить по "счетчику", в котором содержится лексикографический номер
, всегда можно остановить по "счетчику", в котором содержится лексикографический номер  из
из 
Понятие перечислимости можно свести к понятию вычислимости с помощью следующей теоремы [50]: Пусть  и
и 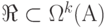 . Множество
. Множество  перечислимо тогда и только тогда, когда существует алфавит
перечислимо тогда и только тогда, когда существует алфавит  и вычислимые функции
и вычислимые функции 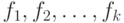 из
из 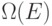 в
в  , такие, что
, такие, что 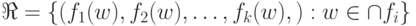 , где теоретико-множественное пере-сечение берется по индексу
, где теоретико-множественное пере-сечение берется по индексу 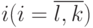 .
.
В частности, при 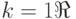 перечислимо в том и только в том случае, когда
перечислимо в том и только в том случае, когда  есть область значений некоторой вычислимой функции.
есть область значений некоторой вычислимой функции.
Доказательство прямого утверждения данной теоремы исходит из того, что если  перечислимо, то для него существует некоторая перечислительная процедура
перечислимо, то для него существует некоторая перечислительная процедура 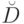 , которая упорядочивает элементы
, которая упорядочивает элементы  в виде однозначно определенной последовательности, геделезация которой приводит к ряду натуральных чисел
в виде однозначно определенной последовательности, геделезация которой приводит к ряду натуральных чисел  . Поэтому искомые вычислительные функции
. Поэтому искомые вычислительные функции  можно определить из
можно определить из  в
в  , для которых вычис-лительная процедура останавливается, когда получен элемент
, для которых вычис-лительная процедура останавливается, когда получен элемент  , что и позволяет считать
, что и позволяет считать 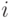 -ю компоненту
-ю компоненту  значением
значением  . Доказательство обратного утверждения строится на том, что если имеется алфавит
. Доказательство обратного утверждения строится на том, что если имеется алфавит  и вычислимые функции
и вычислимые функции  из
из 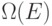 в
в  , такие, что
, такие, что 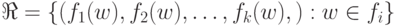 , то всегда можно перечислить множество
, то всегда можно перечислить множество 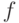 с помощью некоторой перечислительной процедуры
с помощью некоторой перечислительной процедуры 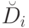 . Эта процедура останавливается тогда, когда получена последовательность
. Эта процедура останавливается тогда, когда получена последовательность 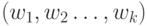 ,
которая является элементом
,
которая является элементом  .
.
Теперь можно перейти от интуитивного к формальному определению перечислимости и условий ее реализации.
Определение 3.3: Множество  называется перечислимым по Тьюрингу ( ПТМ ) в том и только в том случае, когда существует алфавит
называется перечислимым по Тьюрингу ( ПТМ ) в том и только в том случае, когда существует алфавит  и вычислимые по Тьюрингу функции
и вычислимые по Тьюрингу функции 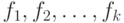 из
из 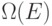 в
в  , такие, что
, такие, что  .
.
Теорема: Множество  перечислимо по Тьюрингу тогда и только тогда, когда существует алфавит
перечислимо по Тьюрингу тогда и только тогда, когда существует алфавит  и вычислимые по Тьюрингу функции
и вычислимые по Тьюрингу функции 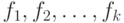 из
из 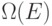 в
в  с общей областью определения
с общей областью определения  , такие, что
, такие, что 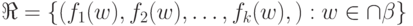 .
.
Для технических нужд больше подходит следующее описание ПТМ : множество  перечислимо по Тьюрингу тогда и только тогда, когда
перечислимо по Тьюрингу тогда и только тогда, когда  есть область определения некоторой ВТФ из
есть область определения некоторой ВТФ из  .
.
При этом следует помнить, что в природе существуют и не перечислимые по Тьюрингу множества, так как натуральный ряд  содержит только счетную совокупность перечислимых по Тьюрингу подмножеств. Однако в большинстве современных вычислительных задач оперируют с конечными множествами, где данное ограничение не работает.
содержит только счетную совокупность перечислимых по Тьюрингу подмножеств. Однако в большинстве современных вычислительных задач оперируют с конечными множествами, где данное ограничение не работает.
Таким образом, приведенных данных достаточно, чтобы утверждать, что по крайней мере в прикладной вычислительной технике любую вычислительную процедуру можно свести к перечислительной, и наоборот.
"Системотехнический" подтекст этого утверждения сводится к тому, что любую функцию можно вычислить только один раз, а полученные результаты представить некоторой таблицей соответствия, которая хранится в ОЗУ и может быть использована многократно. Такое разделение функций характерно для нейрокомпьютерных технологий, где первый этап ( вычислить таблицу соответствия) выполняется "материнской" нейро-ЭВМ, а второй - "дочерней" с тем отличием, что таблица реализуемой функции хранится не в ОЗУ, а представлена в некотором сжатом виде нейросетью, "перечисляющей" строки этой таблицы под воздействием входных сигналов.
3.4. Машины Тьюринга и "количество информации"
Машины Тьюринга изначально предназначались для решения сугубо "внутренних" задач фундаментальной логики и математики. Тем не менее они не только предопределили структурно-функциональную схему реальных вычислителей, но и кардинально изменили сам подход к прикладной математике, где теория вероятности и основанная на ней теория хранения, передачи и преобразования информации играют далеко не последнюю роль. Этот аспект применения машин Тьюринга важен тем, что с помощью оценки "сложности" двоичных последовательностей можно сделать выбор между вычислительным и перечислительным вариантом исполнения машины (фактически между компьютерным и нейрокомпью-терным исполнением). Для этого необходимо оценить эффективность, а с ней и экономическую целесообразность использования конкретной вычислительной машины Тьюринга из множества возможных и конкретной перечислительной машины Тьюринга из множества возможных.
Интуитивно ясно, что для объективного сравнения сначала необходимо "измерить" количество информации, затраченной на предписание, которое задает вычислительный и перечислительный алгоритм, и только после этого сравнить его с количеством "производимой" ими информацией.
Существует три подхода к определению понятия "количество информации" [50], которые совпадают только по единице измерения.
Комбинаторный подход дает ответ на вопрос о количестве бит, которое надо затратить на представление (кодирование) конкретного сообщения. Он основан на следующих соображениях [51]. Имеется переменная  , которая принимает значения, принадлежащие конечному множеству
, которая принимает значения, принадлежащие конечному множеству  , которое состоит из
, которое состоит из  элементов. "Комбинаторная" неопределенность состоит в том, что заранее неизвестно, какое конкретное значение принимает
элементов. "Комбинаторная" неопределенность состоит в том, что заранее неизвестно, какое конкретное значение принимает 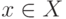 , и эта неопределенность оценивается "энтропией"
, и эта неопределенность оценивается "энтропией"  . Присвоив
. Присвоив 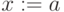 конкретное значение, мы снимаем эту неопределенность, сообщив информацию
конкретное значение, мы снимаем эту неопределенность, сообщив информацию  . Когда переменные
. Когда переменные 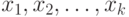 независимо принимают значения из множеств
независимо принимают значения из множеств 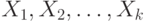 с количеством элементов
с количеством элементов 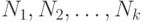 соответственно, выражение для "энтропии" принимает вид:
соответственно, выражение для "энтропии" принимает вид:
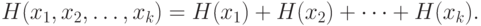 |
( 3.1) |
Отсюда, в рамках комбинаторного подхода:
- Приходится абстрагироваться от вероятностных и тем более содержательных характеристик кодируемой информации, так как в этом случае можно задать только "информационный объем", необходимый для взаимно однозначного кодирования, но не эффективность (коэффициент) его использования с учетом частотных и содержательных характеристик кодируемого сообщения.
- Достаточно просто, зная наиболее общие характеристики сообщения, определить требуемый для кодирования "информационный объем"
![\hat{I} =]I[](/sites/default/files/tex_cache/b92aba26bc7eef5e1a25fee05d0dc57f.png) двоичных символов (бит). Здесь
двоичных символов (бит). Здесь ![] [](/sites/default/files/tex_cache/b803bc2ff18b7c289a5b2502bbd5f390.png) - "старшее целое".
- "старшее целое". - Установить связь между переменными
 и
и 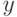 , принадлежащими соответственно
, принадлежащими соответственно  и
и 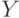 , если под связью понимать, что не все пары
, если под связью понимать, что не все пары 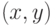 являются "возможными" и принадлежат прямому произведению множеств
являются "возможными" и принадлежат прямому произведению множеств  .
.
В последнем случае считается, что по множеству "возможных" пар  можно (при любом
можно (при любом 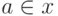 ) определить множества
) определить множества  тех
тех  , для которых
, для которых  . Поэтому условную энтропию естественно определить соотношением:
. Поэтому условную энтропию естественно определить соотношением:
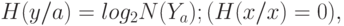 |
( 3.2) |
где 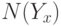 - число элементов в множестве
- число элементов в множестве 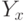 ; а информацию в
; а информацию в  относительно
относительно  соотношением:
соотношением:
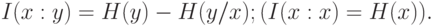 |
( 3.3) |
В (3.2) и (3.3)  входит как "свободная переменная" функций
входит как "свободная переменная" функций 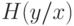 и
и 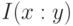 , в то время как
, в то время как  является "связанной переменной". Например, согласно данным табл. 3.3 имеем [51]:
является "связанной переменной". Например, согласно данным табл. 3.3 имеем [51]: 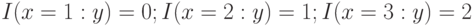 .
.
Вероятностный подход к определению понятия "количество информации" исходит из следующих соотношений:
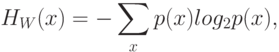 |
( 3.4) |
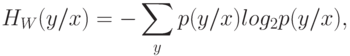 |
( 3.5) |
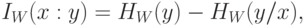 |
( 3.6) |
которые учитывают тот факт, что в этом случае переменные  и
и  являются "случайными" и обладают совместным распределением вероятностей.
являются "случайными" и обладают совместным распределением вероятностей.
В рамках этого подхода по-прежнему  и
и 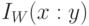 являются функциями от
являются функциями от 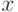 , справедливы неравенства
, справедливы неравенства 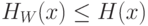 и
и  , где равенство наступает при равномерном законе распределения (на
, где равенство наступает при равномерном законе распределения (на  и на
и на 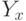 ),
),  и
и 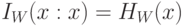 , а величины
, а величины 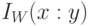 и
и 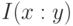 не связаны неравенством определенного знака.
не связаны неравенством определенного знака.
Главное отличие вероятностного от комбинаторного подхода состоит в том, что "теснота связи" между  и
и  характеризуется симметричным соотношением:
характеризуется симметричным соотношением:
![I_{W} (x, y ) = M [ I_{W} (x : y )] = M [ I_{W} (y : x )],](/sites/default/files/tex_cache/4ef43482211e855de009ae96b6489631.png) |
( 3.7) |
где ![M [I_{W} (x : y)]](/sites/default/files/tex_cache/a0a56f67eb58b04e7cacc976856ec1b8.png) и энтропия
и энтропия ![M [ H_{W} (y /x))]](/sites/default/files/tex_cache/7bd90a8c65849c8aee1c5ef5b87454e8.png) являются математическими ожиданиями.
являются математическими ожиданиями.
Переход от 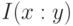 к
к ![M [I_{W} (x : y)]](/sites/default/files/tex_cache/a0a56f67eb58b04e7cacc976856ec1b8.png) обусловлен тем обстоятельством, что только в комбинаторном подходе всегда
обусловлен тем обстоятельством, что только в комбинаторном подходе всегда  , что хорошо согласуется с интуитивным пониманием термина "количество информации". В вероятностном подходе
, что хорошо согласуется с интуитивным пониманием термина "количество информации". В вероятностном подходе  может быть и отрицательной, что интуи-тивно должно восприниматься как "дезинформация". Поэтому в вероятностном подходе подлинной мерой "количества информации" становится осредненная
может быть и отрицательной, что интуи-тивно должно восприниматься как "дезинформация". Поэтому в вероятностном подходе подлинной мерой "количества информации" становится осредненная 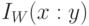 , то есть
, то есть ![M [I_{W} (x : y )]](/sites/default/files/tex_cache/a9283061cc2cc8ebd73edb7a7327d1b4.png) .
.
Вероятностный подход адекватен условиям передачи по каналам связи "массовой" информации, которая представляет собой достаточно большую последовательность слабо или вообще не связанных символов, где проявляются определенные вероятностные закономерности. При этом на практике происходит замена вероятностей эмпирически полученными частотами, что оправдано при решении вопроса о достаточности пропускной способности канала связи на основе знания энтропии потока передаваемых телеграмм и т. п.
Но вероятностный подход теряет смысл при оценке количества информации, содержащейся в тексте "Войны и мира" [51], потому что он требует включить этот роман в совокупность "всевозможных романов" и постулировать в этой совокупности некоторое распределение вероятностей. В этом случае придется рассматривать отдельные сцены "Войны и мира" как некоторую случайную последовательность с быстро затухающими в пределах нескольких страниц "стохастическими связями". Аналогичная ситуация складывается и при оценке количества наследственной информации в генетике, где в результате естественного отбора возникает система согласованных между собой характеристических признаков определенного вида животных или растений.

 \
\ 