|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Методы криптоанализа
Цель лекции
- Рассмотреть возможные исходы криптоанализа
- Изучить методы криптоанализа и их влияние на развитие криптографии
- Оценить предельные возможности по взлому шифров методом полного перебора ключей
- Проанализировать применимость различных типов криптоатак к симметричным и асимметричным криптосистемам и хеш-функциям
- Ознакомиться с перспективными технологиями криптоанализа
Понятие криптоанализа
Криптоанализом (от греческого krypts - "скрытый" и analein - "ослаблять" или избавлять") называют науку восстановления (дешифрования) открытого текста без доступа к ключу. Хотя история криптоанализа насчитывает многие века, особенно интенсивно эта область знаний начала развиваться с наступлением компьютерной эры. Какие методы криптоанализа считаются наиболее эффективными сегодня, и что нас ждет в будущем? Существует ли предельно стойкий шифр, взлом которого является непосильной задачей при любом уровне развития криптоанализа и средств вычислительной техники? В чем отличие научного и практического криптоанализа? На эти и другие вопросы мы постараемся ответить в этой лекции.
Великий сыщик Шерлок Холмс утверждал, что "любая тайна, порожденная человеческим сознанием, им же может быть и раскрыта." Его слова были в середине 40х гг. прошлого века опровергнуты великим ученым и основоположником современной криптографии Клодом Шенноном. Он показал ([6.5]), что если на любой исходный текст наложить (т.е. сложить по модулю с текстом) ключ длины не меньшей, чем само сообщение, то такой шифр будет нераскрываемым: потенциальному злоумышленнику потребуется перебрать все возможные ключи и каждым из них попробовать расшифровать сообщение. Однако использование такого способа шифрования, получившего название "одноразовых блокнотов", в большинстве случаев оказывается слишком дорогим и неоправданным. Это связано с тем, что нет смысла бороться за устойчивость системы защиты информации к взлому ниже некоторой "фоновой" вероятности, т.е. вероятности события, которое мы не в состоянии предотвратить [6.6]. Задача криптоанализа состоит в том, чтобы определить вероятность взлома шифра и, таким образом, оценить его применимость в той или иной области.
Попытка криптоанализа называется атакой. Криптоанализ ставит своей задачей в разных условиях получить дополнительные сведения о ключе шифрования, чтобы значительно уменьшить диапазон вероятных ключей. Результаты криптоанализа могут варьироваться по степени практической применимости. Так, криптограф Ларс Кнудсен [6.7] предлагает следующую классификацию успешных исходов криптоанализа блочных шифров в зависимости от объема и качества секретной информации, которую удалось получить:
- Полный взлом - криптоаналитик извлекает секретный ключ.
- Глобальная дедукция - криптоаналитик разрабатывает функциональный эквивалент исследуемого алгоритма, позволяющий зашифровывать и расшифровывать информацию без знания ключа.
- Частичная дедукция - криптоаналитику удается расшифровать или зашифровать некоторые сообщения.
- Информационная дедукция - криптоаналитик получает некоторую информацию об открытом тексте или ключе.
Взлом шифра не всегда подразумевает обнаружение способа, применимого на практике для восстановления открытого текста по перехваченному зашифрованному сообщению. Допустим, для дешифрования текста методом полного перебора требуется перебрать  возможных ключей ; тогда изобретение способа, требующего для дешифрования
возможных ключей ; тогда изобретение способа, требующего для дешифрования  операций по подбору ключа, будет считаться взломом. В научной криптологии под взломом понимается лишь подтверждение наличия уязвимости криптоалгоритма, свидетельствующее, что свойства шифра не соответствуют заявленным характеристикам. Как правило, криптоанализ начинается с попыток взлома упрощенной модификации алгоритма, после чего результаты распространяются на полноценную версию.
операций по подбору ключа, будет считаться взломом. В научной криптологии под взломом понимается лишь подтверждение наличия уязвимости криптоалгоритма, свидетельствующее, что свойства шифра не соответствуют заявленным характеристикам. Как правило, криптоанализ начинается с попыток взлома упрощенной модификации алгоритма, после чего результаты распространяются на полноценную версию.
Два последних десятилетия ознаменовались резким ростом числа открытых работ по криптологии, а криптоанализ становится одной из наиболее активно развивающихся областей исследований. Появился целый арсенал математических методов, представляющих интерес для криптоаналитика. Кроме того, повышение производительности вычислительной техники сделало возможными такие типы атак, которые раньше были неосуществимы.
Появление новых криптографических алгоритмов приводит к разработке методов их взлома. Если целью криптоаналитика является раскрытие возможно большего числа шифров (независимо от того, хочет ли он этим нанести ущерб обществу, предупредить его о возможной опасности или просто получить известность), то для него наилучшей стратегией является разработка универсальных методов анализа [6.1]. Но эта задача является также и наиболее сложной. Результатом возникновения каждого нового метода криптоанализа является пересмотр оценок безопасности шифров, что, в свою очередь, влечет необходимость создания более стойких шифров. Таким образом, исторические этапы развития криптографии и криптоанализа неразрывно связаны.
На рис.6.1 методы криптоанализа систематизированы по хронологии их появления и применимости для взлома различных категорий криптосистем. Горизонтальная ось разделена на временные промежутки: в область "вчера" попали атаки, которые успешно применялись для взлома шифров в прошлом; "сегодня" - методы криптоанализа, представляющие угрозу для широко используемых в настоящее время криптосистем; "завтра" - эффективно применяемые уже сегодня методы, значение которых в будущем может возрасти, а также методы, которые пока не оказали серьезного влияния на криптологию, однако со временем могут привести прорывам во взломе шифров. На вертикальной оси обозначены области применения методов криптоанализа: для взлома криптосистем с секретным ключом, открытым ключом или хеш-функций.
Прежде чем перейти к рассмотрению изображенных на диаграмме типов криптоаналитических атак, введем ряд понятий и обозначений, которые потребуются нам в дальнейшем: открытый текст будем обозначать буквой  , шифртекст - буквой
, шифртекст - буквой  (в качестве
(в качестве  может выступать любая последовательность битов: текстовый файл, оцифрованный звук, точечный рисунок и т.д.). Пусть для зашифрования и расшифрования используются ключи
может выступать любая последовательность битов: текстовый файл, оцифрованный звук, точечный рисунок и т.д.). Пусть для зашифрования и расшифрования используются ключи  и
и  соответственно (в симметричной криптографии
соответственно (в симметричной криптографии  ); обозначим функцию зашифрования
); обозначим функцию зашифрования  , расшифрования -
, расшифрования -  . Тогда выполняются соотношения
. Тогда выполняются соотношения  .
.
Частотный анализ
На протяжении веков дешифрованию криптограмм помогает частотный анализ появления отдельных символов и их сочетаний. Идея этого метода хорошо известна любителям детективов по рассказу А. Конан Дойля "Пляшущие человечки". Вероятности появления отдельных букв, а также их порядок в словах и фразах естественного языка подчиняются задокументированным статистическим закономерностям: например, пара стоящих рядом букв "ся" в русском языке более вероятна, чем "цы", а "оь" не встречается никогда. Анализируя достаточно длинный текст, зашифрованный методом замены, можно по частотам появления символов произвести обратную замену и восстановить исходный текст.
Как было отмечено выше, каждый метод криптоанализа добавляет новые требования к алгоритмам шифрования. Частотный метод, в котором по распределению символов в шифртексте выдвигаются гипотезы о ключе шифрования, породил требование равномерного распределения символов в шифртексте. Кроме того, принципы частотного анализа сегодня широко применяются в программах по поиску паролей и позволяют сократить перебор в десятки и сотни раз.
Метод полного перебора
С появлением высокопроизводительной вычислительной техники у криптоаналитиков появилась возможность вскрывать шифры методом перебора ключей.
При осуществлении попытки атаки на основе только шифртекста криптоаналитику требуется анализировать выходные данные алгоритма и проверять их "осмысленность". В случае, когда в качестве объекта шифрования выступает графический файл или программа, задача определения "осмысленности" выходных данных становится очень трудной. Если известно, что открытый текст представляет собой предложение на естественном языке, проанализировать результат и опознать успешный исход дешифрования сравнительно несложно, тем более что криптоаналитик зачастую располагает некоторой априорной информацией о содержании сообщения. Задачу выделения осмысленного текста, т.е. определения факта правильной дешифрации, решают при помощи ЭВМ с использованием теоретических положений, разработанных в конце XIX века петербургским математиком Марковым А.А., - цепей Маркова.
Атаки с использованием известного или подобранного открытого текста встречаются чаще, чем можно подумать. В среде криптоаналитиков нельзя назвать неслыханными факты добычи открытого текста шифрованного сообщения или подкупа лица, которое должно будет зашифровать избранное сообщение. Предположим, злоумышленнику известна одна или несколько пар  . Пусть для простоты для любой пары
. Пусть для простоты для любой пары  существует единственный ключ
существует единственный ключ  , удовлетворяющий соотношению
, удовлетворяющий соотношению 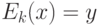 . Примем проверку одного варианта ключа k \in K за одну операцию. Тогда полный перебор ключей потребует
. Примем проверку одного варианта ключа k \in K за одну операцию. Тогда полный перебор ключей потребует 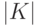 операций, где
операций, где 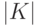 - число элементов в множестве. Если в качестве оценки трудоемкости метода взять математическое ожидание случайной величины, соответствующей числу опробований до момента обнаружения использованного ключа, то мы получим
- число элементов в множестве. Если в качестве оценки трудоемкости метода взять математическое ожидание случайной величины, соответствующей числу опробований до момента обнаружения использованного ключа, то мы получим  операций. Кроме того, алгоритм полного перебора допускает распараллеливание, что позволяет значительно ускорить нахождение ключа.
операций. Кроме того, алгоритм полного перебора допускает распараллеливание, что позволяет значительно ускорить нахождение ключа.
Оценка предельных мощностей взлома
Можно подумать, что с ростом мощности компьютеров разрядность ключа, достаточная для обеспечения безопасности информации против атаки методом полного перебора, будет неограниченно расти. Однако это не так. Существуют фундаментальные ограничения вычислительной мощности, наложенные структурой вселенной: например, скорость передачи любого сигнала не может превышать скорость распространения света в вакууме, а количество атомов во Вселенной (из которых, в конечном счете, состоят компьютеры) огромно, но конечно. Так, например, в [6.4] описаны два фундаментальных ограничения:
- Предел, основанный на выделяемой Солнцем энергии. Все вычисления потребляют энергию. Согласно принципам классической термодинамики и статистической механики, потребление энергии при осуществлении необратимого преобразования (вычисления) имеет порядок
 , где
, где  - температура окружающей среды (по абсолютной шкале Кельвина), а
- температура окружающей среды (по абсолютной шкале Кельвина), а  - постоянная Больцмана (равная
- постоянная Больцмана (равная 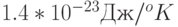 ). Мощность излучения Солнца составляет приблизительно
). Мощность излучения Солнца составляет приблизительно 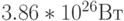 ; таким образом, за весь свой предполагаемый период существования - 10 млрд. лет, или
; таким образом, за весь свой предполагаемый период существования - 10 млрд. лет, или  секунд - Солнце выделит около
секунд - Солнце выделит около  Дж). Предположим, температура окружающей среды
Дж). Предположим, температура окружающей среды  градусов, тогда энергозатраты на одну операцию составляют
градусов, тогда энергозатраты на одну операцию составляют 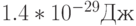 . Значит, количество вычислительных операций, которые можно осуществить с использованием всей выделяемой солнцем энергии, равно выделяемой мощности, поделенной на количество энергии, необходимой для осуществления одной операции, т.е. всего
. Значит, количество вычислительных операций, которые можно осуществить с использованием всей выделяемой солнцем энергии, равно выделяемой мощности, поделенной на количество энергии, необходимой для осуществления одной операции, т.е. всего  операций. Такое количество операций потребовалось бы на взлом ключа из 73 десятичных цифр (или около 250 бит) методом прямого перебора при грубом предположении, что для проверки одного значения ключа необходима всего одна операция (на самом деле - сотни операций). Для справки, количество атомов солнечной системы - около
операций. Такое количество операций потребовалось бы на взлом ключа из 73 десятичных цифр (или около 250 бит) методом прямого перебора при грубом предположении, что для проверки одного значения ключа необходима всего одна операция (на самом деле - сотни операций). Для справки, количество атомов солнечной системы - около 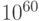 .
. - Предел, основанный на массе Земли. Масса Земли составляет порядка
 кг. Масса протона -
кг. Масса протона -  , т.е. Земля содержит приблизительно
, т.е. Земля содержит приблизительно  протонов. Сопоставим каждому протону отдельный компьютер и примем за скорость выполнения операции на таком компьютере время, за которое луч света проходит расстояние, равное диаметру этого протона (
протонов. Сопоставим каждому протону отдельный компьютер и примем за скорость выполнения операции на таком компьютере время, за которое луч света проходит расстояние, равное диаметру этого протона (  ). Таким образом, каждый компьютер может выполнять
). Таким образом, каждый компьютер может выполнять  операций в секунду. Если все эти компьютеры будут работать параллельно, их суммарное быстродействие составит
операций в секунду. Если все эти компьютеры будут работать параллельно, их суммарное быстродействие составит  операций в секунду, т.е.
операций в секунду, т.е.  . Возраст Вселенной приблизительно 10 млрд. лет, т.е.
. Возраст Вселенной приблизительно 10 млрд. лет, т.е.  секунд. За весь период существования Вселенной такие гипотетические компьютеры размером с протон смогли бы выполнить
секунд. За весь период существования Вселенной такие гипотетические компьютеры размером с протон смогли бы выполнить 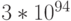 операций. При описанных в п. 1 предположений относительно количества операций, необходимых на проверку значения ключа, такое количество операций позволит взломать ключ длиной 95 десятичных цифр, или 320 бит.
операций. При описанных в п. 1 предположений относительно количества операций, необходимых на проверку значения ключа, такое количество операций позволит взломать ключ длиной 95 десятичных цифр, или 320 бит.
Таким образом, минимальный размер ключа, необходимый для защиты информации от атак злоумышленника, будет расти по мере повышения быстродействия компьютеров; тем не менее, приведенные выше вычисления показывают, что существует возможность выбрать такую длину ключа, что атаку методом полного перебора будет осуществить в принципе невозможно, вне зависимости от повышения вычислительной мощности компьютеров или успехов в области классической теории алгоритмов.


