Введение в лямбда исчисление

Исчислениe

В лямбда-исчислении до сих пор мы познакомились только с лямбда-выражением — нотация полезна для понимания, но все же это далеко не исчисление. Основываясь на нотации, лямбда-исчисление дает замечательную теорию функций и операций над ними. Нам удастся познакомиться только с основными идеями, поскольку детальное рассмотрение не является предметом данной книги.

Лямбда-исчисление дает модель общего понятия — вычисление введением двух основных операций над лямбда-выражениями — альфа-преобразования и бета-редукции (кратко записываемых также как α- и β- ).

Для определения этих понятий нам необходимо отличать два вида вхождений переменных в лямбда-выражение — связанные и свободные вхождения.

Как вы помните, мы говорили, что x, y, ... являются связанными переменными в лямбда-выражении λx: X, y: Y...| e. Тогда нетрудно определить понятие связанного вхождения. Вхождение переменной a в лямбда-выражение является связанным, если:

• a — одна из связанных переменных;
• вхождение является (рекурсивно) связанным вхождением a в e.

Понятие немедленно обобщается на выражение exp, не являющееся лямбда-выражением: вхождение является связанным в exp, если оно является связанным в одном из его лямбда-подвыражений. Например:

[f ; g](λ a : INTEGER | a + f (a, b))

Здесь вхождение a является связанным, но это не так для f, g и b в данном примере — это свободные вхождения. В следующем примере:

λ x: INTEGER | [λ y: INTEGER | x + y + z ]

вхождения x и y связаны, но вхождение z свободно. Неформально это означает, что x и y являются локальными переменными выражениями, в то время как переменная z должна быть определена вне выражения. Это в точности соответствует тому, что мы имеем в программировании:

f (x, y: INTEGER): INTEGER do Result := x + y + z end

Здесь x и y — формальные аргументы, которые означают удобные имена, используемые при определении функции; любые другие имена работали бы точно так же при условии отсутствия конфликта с другими именами. Переменная z имеет другой статус и должна быть определена в контексте. На практике она должна быть компонентом класса — запросом (атрибутом или функцией без аргументов).

Будем говорить, что x "входит связно" в выражение exp, если имеет по меньшей мере одно связанное вхождение в exp, и что "входит свободно", если имеет по меньшей мере одно свободное вхождение в exp, во втором случае x - свободная переменная в exp.

Другим базисным понятием является подстановка.

Определение: подстановка переменной

exp [x:= e]

Например, если exp является:

λz:INTEGER | x + y + z*x

и e — это sin(x), то exp [x:= e] — это выражение λz: INTEGER | sin(x) + y + z *sin(x)

Как показано в примере, выражение может содержать несколько вхождений переменной. Заметьте, подстановка выполняется только для свободных вхождений. Если exp:

λx, z : INTEGER | x + y + z * x

Данное выражение отличается от предыдущего тем, что теперь x является связанной переменной. После аналогичной подстановки exp [x:= e] выражение не изменится, поскольку нет свободных вхождений x. Если exp:

λy : INTEGER | f (x, [λx: INTEGER | x + y])

то подстановка заменит только первое вхождение x, являющееся свободным, но не связанную переменную x лямбда-выражения. Альфа-преобразование прояснит ситуацию.

Но начнем рассмотрения с бета-редукции — центрального правила, охватывающего суть лямбда-нотации. Бета-редукция позволяет нам избавиться от связанной переменной (а следовательно, если нет других переменных, то и от λ ) преобразуя

[λ x : X | exp](e)

в

exp [ x := e]

Это справедливо при условии, что нет свободной переменной выраженияe, связно входящей в exp. Это четко выражает понятие применения функции к фактическим аргументам, так как запись λx:X| exp интуитивно означает, что exp рассматривается как функция с аргументом x и что подстановка выражения e вместо x означает замену всех свободных вхождений x. Вместо слов "бета-редукция трансформирует e в f" будем использовать обозначение

В последнем примере связанная переменная фактически не используется в exp ; в этом случае можно рассматривать лямбда-выражение как константную функцию от x.

Как показывают второй и третий примеры, бета-редукция возможна и в том случае, когда e использует переменные, встречающиеся в exp, лишь бы они были не связанными. Даже третий пример не нарушает ограничение, поскольку в выражении exp (x + y) переменная x не связана — она связана в охватывающем лямбда-выражении, но не в exp. Ограничение имеет место, предотвращая бета-редукцию, только в случаях, подобных данному:

[λx:X| [λy:Y| x + y]] (y)

Здесь редукция приводила бы к выражению λy:Y|y+y, что некорректно, так как порождало бы новые вхождения связанной переменной, не соответствующие неформальному пониманию лямбда-выражения.

Значит ли это, что в подобных случаях бета-редукция невозможна по той причине, что нам не повезло с именем? Это было бы огорчительно, так как имена связанных переменных произвольны и их можно выбирать, не меняя общего смысла. Если мы заменим [6.6] на:

[λx:X| [λz:y|x + z]] (y)

то бета-редукция становится возможной, давая результат λz: Y| y+ z.

В программировании мы делаем то же самое, когда выбираем новое имя для формального аргумента метода, если оно конфликтует с именем атрибута класса.

Для узаконивания таких безвредных изменений связанных переменных нам необходимо второе правило — альфа-преобразование. Для заданной переменной y альфа-преобразование трансформирует лямбда-выражение

λx:X,...| exp

В котором у не имеет ни свободных, ни связанных вхождений в выражение

λy : X, ... | exp [x :=y]

Условие, налагаемое на y, защищает от замены x на y в обоих ниже приведенных случаях:

λx : X|x+y

λy : X | x + y]

При замене результирующее выражение λy: Y | y + y потеряло бы семантику, которая подразумевается в исходном выражении.

• [6.7] представляет функцию одного аргумента, возвращающую значение y, к которому добавлено значение, переданное функции в качестве аргумента. Для этой функции y — свободная переменная, определенная в контексте выражения (например, в охватывающем выражении). Если же в данном случае подстановка была бы допустимой, то полученное выражение задавало бы функцию, удваивающую значение переданного ей аргумента. Две функции полностью различны!
• В [6.8]y связано, но тогда альфа-преобразование сливало бы y со свободной переменной x.

Последнее наблюдение показывает, что требование на y избыточно, так как в [6.8] предварительно y можно переименовать.

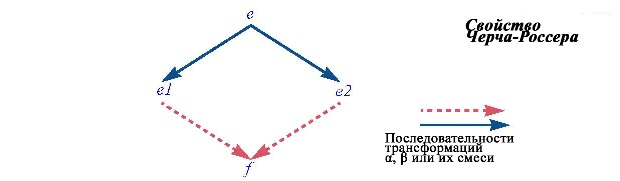
Альфа-преобразование и бета-редукция дают основу для полностью проработанной теории вычислений, описывающей любые вычисления как последовательность таких преобразований (возможно, сложную) лямбда-выражений. Фундаментальное свойство согласованности этой теории выражает теорема Черча — Россера.

Теорема гласит, что если из данного лямбда-выражения exp две различные последовательности трансформаций приводят к различным выражениям expl и exp2, то существуют две другие последовательности трансформаций, которые приводят оба эти выражения к единому выражению f. Это означает, что, если возможны некоторые трансформации для любого частного выражения, то не имеет значения, с какого преобразования начинать, поскольку в конечном итоге придем к одной и той же канонической форме.

Рис. 6.2. Свойство Черча - Россера