|
Есть такие задания, и они никак не принимаются. Притом ошибки только по этим заданиям, в какой бы последовательности я их не заполнял. Как их заполнять??? Инструкций в заданиях нет. Там через запятые, подряд как число, через пробел, или надо текст весь писать через запятую или точку? Задание: Пронумеруйте шаги Создание имени путем выделения ячеек на листе: |
Средства для обработки массивов
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Часто при работе с таблицами возникает необходимость применить одну и ту же операцию к целому диапазону ячеек или произвести расчеты по формулам, зависящим от большого массива данных.
Под массивом в MS Excel понимается прямоугольный диапазон формул или значений, которые программа обрабатывает как единую группу. MS Excel предоставляет простое и элегантное средство – формула массива – для решения подобных задач.
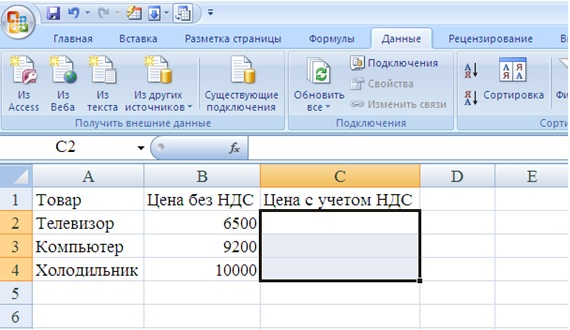
В качестве примера использования формулы массива приведем расчет цен группы товаров с учетом НДС. Например, в диапазоне В2:В4 даны цены группы товаров без учета НДС. Необходимо найти цену каждого товара с учетом НДС (который будем полагать равным 25%). Таким образом, необходимо умножить массив элементов В2:В4 на 125%. Результат надо разместить в ячейках диапазона С2:С4 (рис. 17.1 рис. 17.1). Для этого:
- Выберите диапазон, например С2:С4, в котором будет размещен результат умножения первоначального массива на число. От диапазона, в котором будет находиться результат, требуется, чтобы он имел тот же размер, что и исходный диапазон (рис. 17.1 рис. 17.1).
- Введите формулу
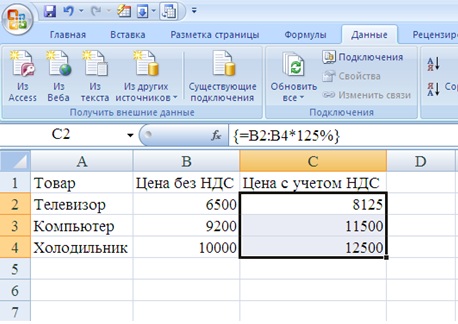
= В2:В4*125%
- Завершите ввод формулы не нажатием клавиши <Enter>, а нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. Таким образом, вы сообщите MS Excel, что необходимо выполнить операцию над массивом, т. е. создать формулу массива. В ответ MS Excel автоматически возьмет формулу в фигурные скобки (рис. 17.2 рис. 17.2):
{=В2:В4*125%}
Примечание. При выборе диапазона, в который будет введена формула массива, надо быть аккуратным. Если выбрать слишком маленький диапазон, то невозможно будет получить все результаты. Если диапазон выбрать слишком большим, то в неиспользуемых ячейках отобразится сообщение об ошибке #Н/Д.
Исправление формулы массива
Формулы массивов действуют на все ячейки массива. Нельзя изменять отдельные ячейки в операндах формулы. Как же изменить формулу массива? Самый простой способ – выделить весь диапазон, в который введена формула массива, и удалить ее, нажав клавишу <Delete>. После чего ввести формулу массива корректно. Такой прямой способ хорош, когда формула простая. А если она сложная, а в ней просто требуется произвести какую-то небольшую коррекцию? В этом случае возможны две ситуации.
- Формула массива введена в правильный диапазон. Тогда надо выделить этот диапазон. В строке формул произвести требуемые изменения и завершить ввод исправленной формулы нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.
- Формула массива введена в неправильный диапазон. В этом случае надо выделить этот диапазон, в строке формул выделить формулу и скопировать ее в буфер обмена. Затем повторно выбрать диапазон и удалить из него формулу массива. После этого надо выделить корректный диапазон, расположить в строке формул курсор и вставить в нее формулу из буфера обмена. Произвести, если требуется, необходимое исправление формулы и завершить ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.
Поэлементное сложение, вычитание, умножение и деление двух массивов
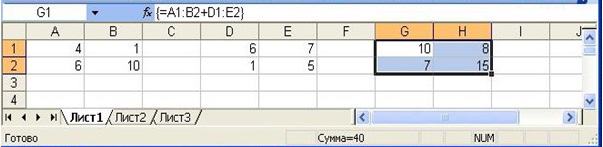
Продемонстрируем операцию поэлементного сложения двух массивов. Пусть, например слагаемыми будут массивы, содержащиеся в диапазонах А1:В2 и D1:E2 (рис. 17.3 рис. 17.3).
Далее:
- Выберите на рабочем листе диапазон, например Gl:H2, в который будет помещен результат поэлементного сложения двух массивов. От данного диапазона требуется, чтобы он имел тот же размер, что и массивы-слагаемые.
- Введите формулу = A1:B2+D1:E2
- Завершите ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. MS Excel возьмет формулу в строке формул в фигурные скобки (рис 17.3) и произведет требуемые вычисления {=A1:B2+D1:E2}
Примечание. Для избежания ошибок в формулу вводите ссылки на диапазоны ячеек не с клавиатуры, а путем выбора их на рабочем листе мышью. Тогда ссылка на диапазон ячеек в формулу будет вводиться автоматически.
Аналогично можно вычислить поэлементно разность, произведение и деление массивов.
Вычисление функции, зависящей от элементов массива
На рабочем листе допустимо создавать формулы массива, каждый элемент которого связан посредством некоторой функции с соответствующим элементом первоначального массива.
Например, пусть в диапазоне А1:В2 имеется некоторый массив данных. Требуется найти массив, элементы которого равны значениям функции SIN от соответствующих элементов искомого массива.
Для этого:
- Выберите в рабочем листе диапазон, например D1:E2, в котором будет размещен результат. От данного диапазона требуется, чтобы он имел тот же размер, что и исходный диапазон.
- Введите формулу =SIN(A1:B2)
- Завершите ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. MS Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления с элементами массива {=SIN(A1:B2)}
Вычисление сложных выражений
Приведем более сложный пример использования формул массива. А именно, попытаемся найти значение следующего выражения:
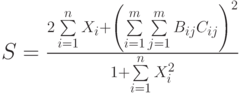
где: X – вектор из n компонентов, B и C – матрицы размерности mxm, причем, n=3, m=2 и
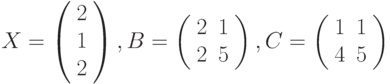
Для решения этой задачи нам потребуется функция рабочего листа СУММ (SUM), которая суммирует все числа из диапазона ячеек.
Синтаксис:
СУММ{число1; число2; ...).
где: число1, число2, ... – это от 1 до 30 аргументов, которые надо просуммировать. Аргументами могут быть либо ссылки на диапазоны ячеек, либо числа.
Например, СУММ(3;2) возвращает 5. Если в диапазоне ячеек А1:В2 содержатся числа 1, 2, 3, 4, то СУММ(А1:В2;15) возвращает 25.
Теперь можно вернуться к вычислению значения s.
- Введите в диапазон А2:А4 компоненты вектора X.
- Введите в диапазон В2: С3 компоненты матрицы В.
- Введите в диапазон D2:ЕЗ компоненты матрицы С.
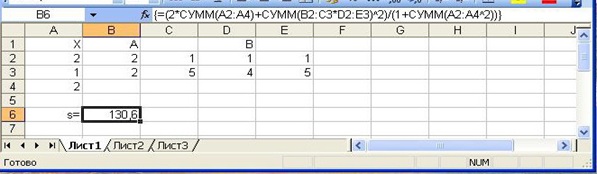
- Введите в ячейку В6 следующую формулу:
=(2*СУММ(А2:А4)+СУММ(В2:СЗ*D2:Е3) ^2) / (1+СУММ(А2 :А4^2))
- Завершите ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. MS Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления (рис. 17.4 рис. 17.4)
{=(2*СУММ(А2:А4)+СУММ(В2:СЗ*D2:ЕЗ) ^2) / (1+СУММ(А2 :А4^2))}
Примечание. Хотя в данном примере формула возвращает одно число, а не массив, тем не менее формула является формулой массива. Поэтому не забудьте ее ввод завершить нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. Если вы это не сделаете, в ячейке В6 появится сообщение об ошибке #ЗНАЧ!.
Конечно, этот же результат можно было бы получить и без использования формул массивов, введя в ячейку В6 простую формулу
=(2*СУММ(А2:А4)+СУММПРОИЗВ(В2:СЗ;D2:ЕЗ)^2)/(1+СУММКВ(А2:А4))
В данной формуле используются функции рабочего листа СУММПРОИЗВ (SUMPRODUCT) и СУММКВ (SUMSQ).
Функция СУММПРОИЗВ возвращает сумму произведений соответствующих элементов массивов.
Синтаксис:
СУММПРОИЗВ (массив1; массив2; ...).
где: массив1, массив2, ... – это от 2 до 30 массивов, чьи компоненты нужно перемножить, а затем сложить. Аргументы, которые являются массивами, должны иметь одинаковые размерности. Если это не так, то функция СУММПРОИЗВ возвращает значение ошибки #ЗНАЧ!.
Функция СУММКВ возвращает сумму квадратов аргументов.
Синтаксис:
СУММКВ (число1; число2; ...).
где: число1, число2, ... – это от 1 до 30 аргументов, квадраты которых суммируются. Можно использовать отдельный массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.
Функции рабочего листа для работы с матрицами
В MS Excel имеются функции рабочего листа для работы с матрицами, перечисленные в табл. 17.1 таблица 17.1.
| Функция (рус.) | Функция (англ.) | Описание |
|---|---|---|
| МОБР (массив) | MINVERSE (array) | Возвращает обратную матрицу |
| МОПРЕД (массив) | MDETERM (array) | Возвращает определитель матрицы |
| МУМНОЖ (массив1; массив2) | MMULT (array1; array2) | Возвращает матричное произведение двух матриц |
| ТРАНСП (массив) | TRANSPOSE (array) | Возвращает транспонированную матрицу |
Примечание 1. При работе с матрицами, перед вводом формулы, надо выделить область на рабочем листе, куда будет помещен результат вычислений, а ввод формулы завершать нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.
Примечание 2. Массивы в формулах могут быть заданы либо как диапазон ячеек, например А1:С3, либо как массив констант, например {1;2;3: 4;5;6: 7;8;9}, либо как имя диапазона или массива.
Решение системы линейных уравнений
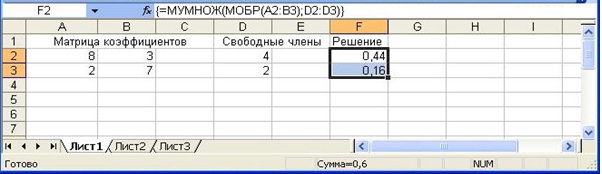
Решим в качестве примера систему линейных уравнений с двумя неизвестными, матрица коэффициентов которой записана в ячейки А2:В3, а свободные члены – в ячейки D2:D3 (рис. 17.5 рис. 17.5).
Вспомним, что решение линейной системы АХ = В,
где: А – матрица коэффициентов,
В – столбец (вектор) свободных членов,
X– столбец (вектор) неизвестных, имеет вид X = А-1В , где А-1– обратная матрица к А.
В нашем случае
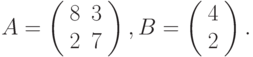
Поэтому, для решения системы уравнений
- Выберите тот диапазон, в который будет введено решение. Например, F2: F3.
- Введите в него формулу =МУМНОЖ(МОБР(А2:В3);D2:D3)
- Завершите ввод формулы нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.
- MS Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления с элементами массива (рис. 17.5 рис. 17.5).
{=МУМНОЖ(МОБР(А2:В3);D2:D3)}
Таким образом, решением системы уравнений является вектор
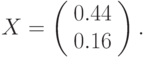
В качестве более сложного примера решим систему линейных уравнений А2Х = В, где
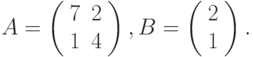
Решением этой системы является вектор X = (А2)-1В.
Для нахождения вектора X.
- Введите элементы матрицы А в диапазон ячеек А2:В3.
- Введите элементы вектора В в диапазон ячеек D2: D3.
- Выберите диапазон F2:F3, куда поместим элементы вектора решения.
- Введите в этот диапазон формулу:
=МУМНОЖ(МОБР(МУМНОЖ(А2:В3;А2:ВЗ));D2:D3)
- Завершите ввод формулы нажатием комбинации клавиш <Ctrl>+<Shift>+ +<Enter>. MS Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления с элементами массива.
{=МУМНОЖ(МОБР(МУМНОЖ(А2:В3;А2:ВЗ));D2:D3)}
В диапазоне ячеек F2:F3 будет найдено решение системы уравнений
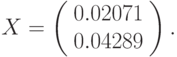
Нахождение значения квадратичной формы
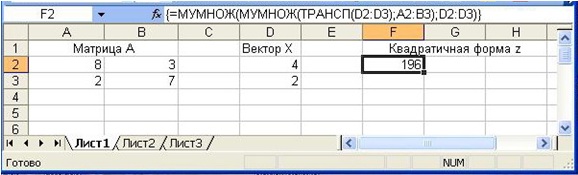
Рассмотрим пример вычисления квадратичной формы z = XТАХ, при этом
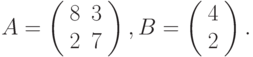
Для нахождения значения этой квадратичной формы:
- Введите элементы матрицы А в диапазон ячеек А2:В3 (рис. 17.6 рис. 17.6).
- Введите элементы вектора Х в диапазон ячеек D2:D3.
- Выберите ячейку F2, куда необходимо поместить значение квадратичной формы.
- Введите в эту ячейку формулу
=МУМНОЖ(МУМНОЖ(TPAHCП(D2:D3);A2:B3);D2:D3)
- Завершите ввод формулы нажатием комбинации клавиш <Ctrl>+<Shift>+ +<Enter>. MS Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления с элементами массивов (рис. 17.6 рис. 17.6).
{=МУМНОЖ(МУМНОЖ(TPAHCП(D2:D3);A2:B3);D2:D3)}
Примечание. Хотя в данном примере формула возвращает одно число, а не массив, тем не менее, она является формулой массива. Поэтому не забудьте ее ввод завершить нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. Если вы это не сделаете, в ячейке F2 появится сообщение об ошибке #ЗНАЧ!.
Пошаговое решение системы линейных уравнений методом Гаусса
Хорошим упражнением по работе с массивами является пошаговое программирование на рабочем листе решения системы линейных уравнений методом Гаусса.
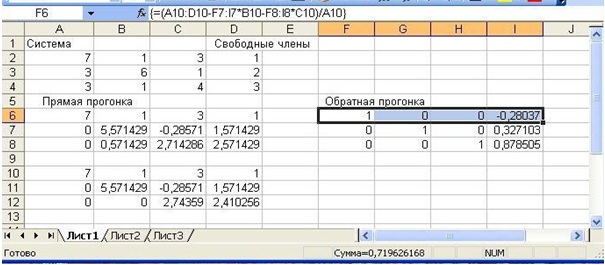
На рисунке 17.7 рис. 17.7 приведены результаты пошагового решения методом Гаусса следующей системы линейных уравнений:
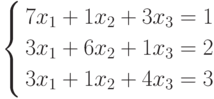
Итак, для пошагового решения этой системы уравнений сначала введите на рабочем листе исходные данные. Для этого:
- В ячейки диапазона А2:С4 введите коэффициенты системы, стоящие при неизвестных.
- В ячейках диапазона D2: D4 задайте свободные члены.
- Приступим к прямой прогонке метода Гаусса:
- Через буфер обмена скопируйте диапазон А2:D2 на А6:D6.
- Выберите диапазон А7:D7.
- Введите в него следующую формулу и завершите ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.
{=А3:D3-$A$2:$D$2*A3/$A$2}
- Выберите диапазон A7:D7, расположите указатель мыши на маркере заполнения этого диапазона и пробуксируйте его вниз на одну строку.
- Выделите диапазон А6: D7 и скопируйте его содержимое в буфер обмена.
- Выберите ячейку А10.
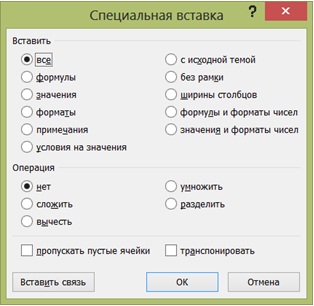
- Щелкните правой кнопкой мыши Специальная вставка. На экране отобразится диалоговое окно Специальная вставка (рис. 17.8 рис. 17.8). Выберите переключатель значения в группе Вставить и нажмите кнопку ОК. В результате в диапазон A10:D10 из диапазона А6:D7 будут скопированы только значения, а не формулы.
- Выделите диапазон A12:D12.
- Введите в него следующую формулу и завершите ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.
{=A8:D8-A7:D7*B8/B7}
Примечание. Команда Щелкните правой кнопкой мыши Специальная вставка удобна при копировании и вставке части атрибутов ячеек, таких как формат или значение. Команда позволяет комбинировать в одной ячейке атрибуты из разных ячеек, а также выполнять над ними арифметические операции. Кроме того, установка флажка транспонировать позволяет вставлять в рабочий лист данные из буфера обмена с одновременным их транспонированием. А установка флажка пропускать пустые ячейки разрешает игнорировать пустые ячейки при вставке в рабочий лист Данных из буфера обмена.
Прямая прогонка метода Гаусса закончилась. Переходим к обратной прогонке.
- Выберите диапазон F8:I8.
- Введите в него следующую формулу и завершите ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.
{=A12:D12/C12}
- Выделите диапазон F7:I7.
- Введите в него следующую формулу и завершите ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.
{=(А11:D11-F8:I8*C11)/B11}
- Выберите диапазон F6:I6.
- Введите в него следующую формулу и завершите ее ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.
{=(А10:D10-F7:I7*B10-F8:I8*C10)/A10}
Итак, решением системы уравнений является следующий вектор
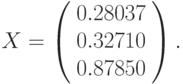
Использование формулы массива для исключения промежуточной формулы
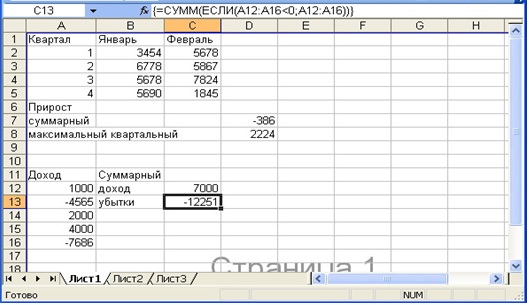
Использование формулы массива может избавить от необходимости вводить на рабочем листе промежуточные формулы. Продемонстрируем это на примере. На рисунке 17.9 рис. 17.9 приведена некоторая отчетная ведомость.
Необходимо найти:
- суммарный прирост, скажем, по продажам в феврале по сравнению с январем. Для этого достаточно ввести в ячейку D7 формулу массивов:
{=СУММ(С2:С5-В2:В5)}
- максимальный квартальный прирост по продажам в феврале по сравнению с январем. Для этого достаточно ввести в ячейку D8 формулу массивов:
{=МАКС(С2:С5-В2:В5)}
Примечание. Здесь используется формула рабочего листа МАКС (MAX), которая возвращает максимальное значение среди ее аргументов. Функция МИН (MIN) возвращает минимальное значение среди ее аргументов.
В случае если среди данных имеются как положительные, так и отрицательные значения, формулы массивов позволяют обработать только положительные или отрицательные данные без предварительной их сортировки или фильтрации. Например, пусть в диапазон А12:А16 введены как доходы, так и убытки за отчетный период. Тогда, для того чтобы найти:
- суммарный доход, достаточно ввести в ячейку С12 формулу массивов:
{=СУММ(ЕСЛИ(А12:А16>0;А12:А16))}
- суммарный убыток, достаточно ввести в ячейку С13 формулу массивов:
{=СУММ(ЕСЛИ(А12:А16<0;А12:А16))}
ЗАДАНИЯ
Вариант 1.
- Решить системы линейных уравнений АХ = В, А3Х = В и вычислить значение квадратичной формы z=YTATA2Y , где
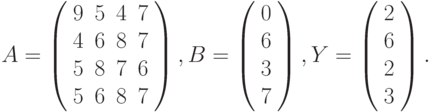
- Вычислить
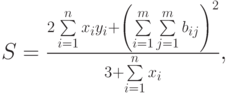
где: х, у – векторы из n компонентов, b – матрица размерности mxm, причем n = 4, m = 2 и
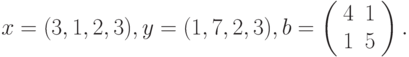
Вариант 2.
- Решить системы линейных уравнений АХ = В, А2АTХ = В и вычислить значение квадратичной формы z=YTA3Y , где
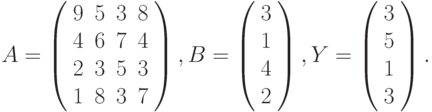
- Вычислить
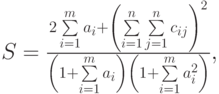
где: a – вектор из m компонентов, с – матрица размерности nxn, причем
n = 3, m = 4
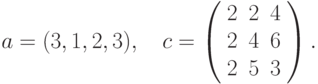
Вариант3.
- Решить системы линейных уравнений АХ = В, ААTАХ = В и вычислить значение квадратичной формы z=YTATA3Y, где
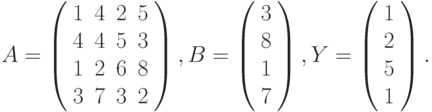
- Вычислить
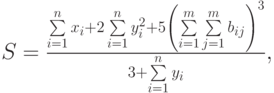
где: x, y – векторы из n компонентов, b – матрица размерности mxm, причем n = 4, m = 2 и
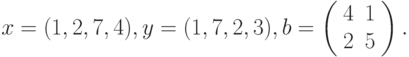
Вариант4.
- Решить системы линейных уравнений АХ = B, А2АTАХ = В и вычислить значение квадратичной формы z=YTATAATY , где
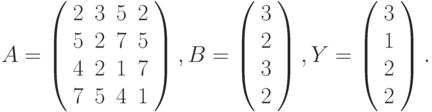
- Вычислить
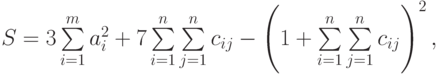
где: а – вектор из m компонентов, с – матрица размерности nхn, причем
n = 3, m = 4 и
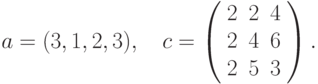
Вариант5.
- Решить системы линейных уравнений АХ = В, ААTА2Х = B и вычислить значение квадратичной формы z=YTA3ATY , где
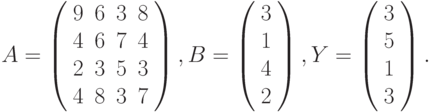
- Вычислить
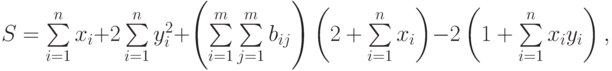
где: х, у – векторы из n компонентов, b – матрица размерности mxm, причем n = 4, m = 2 и
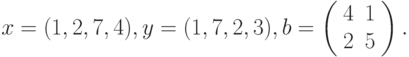
Вариант6.
- Решить системы линейных уравнений АХ = В, А3АTХ = В и вычислить значение квадратичной формы z=YTA2ATAY , где
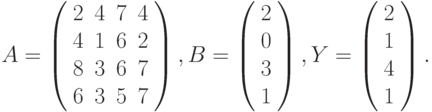
- Вычислить
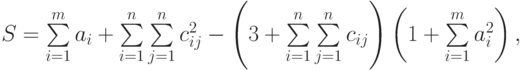
где: а – вектор из m компонентов, с – матрица размерности nxn, причем
n = 3, m = 4 и
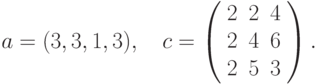
Вариант7.
- Решить системы линейных уравнений АХ = В, АTА3Х = В и вычислить значение квадратичной формы z=YTAATA2Y , где
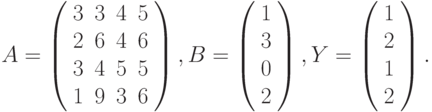
- Вычислить
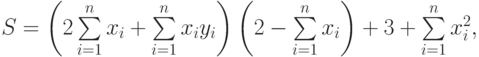
где: х, y – векторы из n компонентов, причем n = 4 и x=(1, 2, 7, 4), y=(1, 7, 2, 3).
Вариант8.
- Решить системы линейных уравнений АХ = В, ААTА2Х = В и вычислить значение квадратичной формы z=YTA2ATAY , где
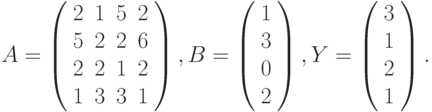
- Вычислить
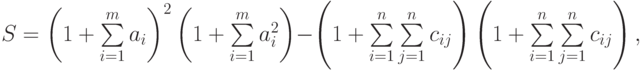
где: а – вектор из m компонентов, с – матрица размерности пxп, причем
n = 2, m = 4 и
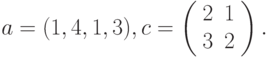
Вариант9.
- Решить системы линейных уравнений АХ = В, АTААTX = В и вычислить значение квадратичной формы z=YTAATAATY , где
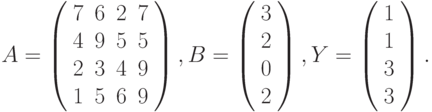
- Вычислить
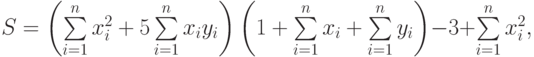
где: x, y – векторы из n компонентов, причем n = 4 и х=(7, 5, 7, 4), у=(2, 4, 2, 3).
Вариант10.
- Решить системы линейных уравнений АХ = В, A2ATAX = B и вычислить значение квадратичной формы z=YTAATAATY , где
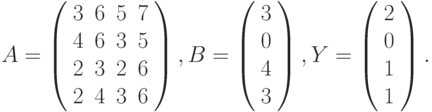
- Вычислить
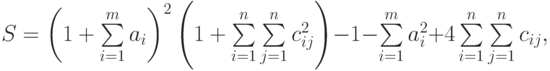
где: а – вектор из m компонентов, с –матрица размерности nхn, причем
n = 3, m = 4