Решение задач нейронными сетями
Шаг алгоритма разбивается на два этапа:
- 1-й этап - для фиксированного набора ядер a1,...,ak ищем минимизирующее критерий качества D разбиение
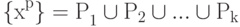 ; оно дается решающим правилом:
; оно дается решающим правилом: 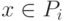 , если d(x, ai)<d(x, aj) при
, если d(x, ai)<d(x, aj) при  , в том случае, когда для x минимум d(x,a) достигается при нескольких значениях i, выбор между ними может быть сделан произвольно;
, в том случае, когда для x минимум d(x,a) достигается при нескольких значениях i, выбор между ними может быть сделан произвольно; - 2-й этап - для каждого Pi ( i=1,...,k ), полученного на первом этапе, ищется
 , минимизирующее критерий качества (т.е. слагаемое в D для данного
, минимизирующее критерий качества (т.е. слагаемое в D для данного 
Начальные значения a1,...,ak, 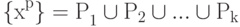 выбираются произвольно, либо по какому-нибудь эвристическому правилу.
выбираются произвольно, либо по какому-нибудь эвристическому правилу.
На каждом шаге и этапе алгоритма уменьшается критерий качества D, отсюда следует сходимость алгоритма - после конечного числа шагов разбиение 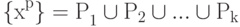 уже не меняется.
уже не меняется.
Если ядру ai сопоставляется элемент сети, вычисляющий по входному сигналу x функцию d(x,ai), то решающее правило для классификации дается интерпретатором "победитель забирает все": элемент x принадлежит классу Pi, если выходной сигнал i -го элемента d(x,ai) меньше всех остальных
Единственная вычислительная сложность в алгоритме может состоять в поиске ядра по классу на втором этапе алгоритма, т.е. в поиске 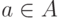 , минимизирующего
, минимизирующего 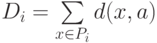
В связи с этим, в большинстве конкретных реализаций метода мера близости d выбирается такой, чтобы легко можно было найти a, минимизирующее D для данного P.
В простейшем случае пространство ядер A совпадает с пространством векторов x, а мера близости d(x,a) - положительно определенная квадратичная форма от x-a, например, квадрат евклидового расстояния или другая положительно определенная квадратичная форма. Тогда ядро ai, минимизирующее Di, есть центр тяжести класса Pi:
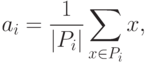 |
( 17) |
где |Pi| - число элементов в Pi.
В этом случае также упрощается и решающее правило, разделяющее классы. Обозначим d(x,a) =(x-a,x-a), где (.,.) - билинейная форма (если d - квадрат евклидового расстояния между x и a, то (.,.) - обычное скалярное произведение). В силу билинейности
d(x,a)=(x-a,x-a)=(x,x)-2(x,a) +(a,a).
Чтобы сравнить d(x,ai) для разных i и найти среди них минимальное, достаточно вычислить линейную неоднородную функцию от x:
d1(x,ai) = (ai,ai)-2(x,ai).
Минимальное значение d(x,ai) достигается при том же i, что и минимум d1(x,ai), поэтому решающее правило реализуется с помощью k сумматоров, вычисляющих d(x,a) и интерпретатора, выбирающего сумматор с минимальным выходным сигналом. Номер этого сумматора и есть номер класса, к которому относится x.
Пусть теперь мера близости - коэффициент корреляции между вектором данных и ядром класса:
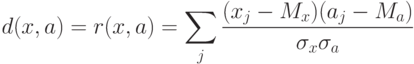
где  - координаты векторов,
- координаты векторов, 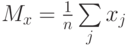 (и аналогично
(и аналогично 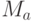 ), n - размерность пространства данных,
), n - размерность пространства данных,  (и аналогично
(и аналогично  ).
).
Предполагается, что данные предварительно обрабатываются (нормируются и центрируются) по правилу:

Точно также нормированы и центрированы векторы ядер a. Поэтому все обрабатываемые векторы и ядра принадлежат сечению единичной евклидовой сферы ( ||x||=1 ) гиперплоскостью ( 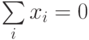 ). В таком случае
). В таком случае  .
.
Задача поиска ядра для данного класса P имеет своим решением
 |
( 18) |
В описанных простейших случаях, когда ядро класса точно определяется как среднее арифметическое (или нормированное среднее арифметическое) элементов класса, а решающее правило основано на сравнении выходных сигналов линейных адаптивных сумматоров, нейронную сеть, реализующую метод динамических ядер, называют сетью Кохонена. В определении ядер a для сетей Кохонена входят суммы 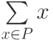 . Это позволяет накапливать новые динамические ядра, обрабатывая по одному примеру и пересчитывая ai после появления в Pi нового примера. Сходимость при такой модификации, однако, ухудшается.
. Это позволяет накапливать новые динамические ядра, обрабатывая по одному примеру и пересчитывая ai после появления в Pi нового примера. Сходимость при такой модификации, однако, ухудшается.
Закончим раздел рассмотрением различных способов использования полученных классификаторов.
- Базовый способ: для вектора данных xi и каждого ядра ai вычисляется yi=d(x,ai) (условимся считать, что правильному ядру отвечает максимум d, изменяя, если надо, знак d ); по правилу "победитель забирает все" строка ответов yi преобразуется в строку, где только один элемент, соответствующий максимальному yi, равен 1, остальные - нули. Эта строка и является результатом функционирования сети. По ней может быть определен номер класса (номер места, на котором стоит 1 ) и другие показатели.
- Метод аккредитации: за слоем элементов базового метода, выдающих сигналы 0 или 1 по правилу "победитель забирает все" (далее называем его слоем базового интерпретатора), надстраивается еще один слой выходных сумматоров. С каждым ( i -м) классом ассоциируется q -мерный выходной вектор zi с координатами zij. Он может формироваться по-разному: от двоичного представления номера класса до вектора ядра класса. Вес связи, ведущей от i -го элемента слоя базового интерпретатора к j -му выходному сумматору определяется в точности как zij. Если на этом i -м элементе базового интерпретатора получен сигнал 1, а на остальных - 0, то на выходных сумматорах будут получены числа zij.
-
Нечеткая классификация. Пусть для вектора данных x обработан слоем элементов, вычисляющих yi=d(x,ai). Идея дальнейшей обработки состоит в том, чтобы выбрать из этого набора {yi} несколько самых больших чисел и после нормировки объявить их значениями функций принадлежности к соответствующим классам. Предполагается, что к остальным классам объект наверняка не принадлежит. Для выбора семейства G наибольших yi определим следующие числа:

где число
 характеризует отклонение "уровня среза" s от среднего значения
характеризует отклонение "уровня среза" s от среднего значения 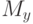
![\alpha \in {\rm{[ - 1}}{\rm{,1]}}](/sites/default/files/tex_cache/823c16d63b3dfadc0122407c9a98bcab.png) , по умолчанию обычно принимается
, по умолчанию обычно принимается 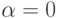 .
.Множество
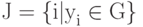 трактуется как совокупность номеров тех классов, к которым может принадлежать объект, а нормированные на единичную сумму неотрицательные величины
трактуется как совокупность номеров тех классов, к которым может принадлежать объект, а нормированные на единичную сумму неотрицательные величины
(при
 и f = 0 в противном случае)
и f = 0 в противном случае)интерпретируются как значения функций принадлежности этим классам.
-
Метод интерполяции надстраивается над нечеткой классификацией аналогично тому, как метод аккредитации связан с базовым способом. С каждым классом связывается q -мерный выходной вектор zi. Строится слой из q выходных сумматоров, каждый из которых должен выдавать свою компоненту выходного вектора. Весовые коэффициенты связей, ведущих от того элемента нечеткого классификатора, который вычисляет fi, к j -му выходному сумматору определяются как zij. В итоге вектор выходных сигналов сети есть
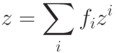
В отдельных случаях по смыслу задачи требуется нормировка fi на единичную сумму квадратов или модулей.
Выбор одного из описанных четырех вариантов использования сети (или какого-нибудь другого) определяется нуждами пользователя. Предлагаемые четыре способа покрывают большую часть потребностей.
За пределами этой лекции остался наиболее универсальный способ обучения нейронных сетей методами гладкой оптимизации - минимизации функции оценки. Ему посвящена "Быстрое дифференцирование, двойственность и обратное распространение ошибки" .
Работа над лекцией была поддержана Красноярским краевым фондом науки, грант 6F0124.
