Решение задач нейронными сетями

Приведем это решение в традиционных обозначениях математической статистики. Обозначим M_о среднее значение j -й координаты векторов исходной выборки:

Пусть M - вектор с координатами M_о. Введем также обозначение s_j для выборочного среднеквадратичного отклонения:

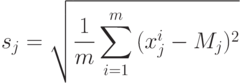
Величины s_j задают естественный масштаб для измерения j -х координат векторов x. Кроме того, нам потребуются величина s_f и коэффициенты корреляции f с j -ми координатами векторов x - r_fj:

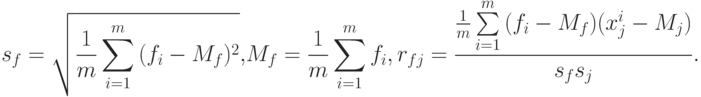
Вернемся к n -мерным векторам данных и коэффициентов. Представим, что векторы сигналов проходят предобработку - центрирование и нормировку и далее мы имеем дело с векторами yⁱ:

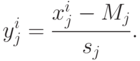
Это, в частности, означает, что все рассматриваемые координаты вектора x имеют ненулевую дисперсию, т.е. постоянные координаты исключаются из рассмотрения - они не несут полезной информации. Уравнения регрессии будем искать в форме: . Получим:

( 3)

где R_f - вектор коэффициентов корреляции f с j -ми координатами векторов x, имеющий координаты r_fj, R - матрица коэффициентов корреляции между координатами вектора данных:

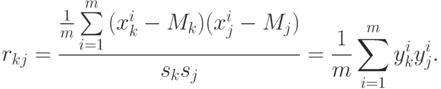
В задачах обработки данных почти всегда возникает вопрос о последовательном уточнении результатов по мере поступления новых данных ( обработка данных "на лету" ). Существует, как минимум, два подхода к ответу на этот вопрос для задачи линейной регрессии. Первый подход состоит в том, что изменения в коэффициентах регрессии при поступлении новых данных рассматриваются как малые и в их вычислении ограничиваются первыми порядками теории возмущений. При втором подходе для каждого нового вектора данных делается шаг изменений коэффициентов, уменьшающий ошибку регрессии 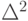на вновь поступившем векторе данных. При этом "предыдущий опыт" фиксируется только в текущих коэффициентах регрессии.

В рамках первого подхода рассмотрим, как будет изменяться из формулы (2) при добавлении нового вектора данных. В первом порядке теории возмущений найдем изменение вектора коэффициента при изменении вектора p и матрицы Q:

Пусть на выборке 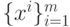вычислены p, Q, Q^-1. При получении нового вектора данных x^{m +1} и соответствующего значения F(x^{m +1})=f _{m +1} имеем ^{1Напомним, что для векторов x, y матрица имеет своими элементами .} :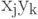

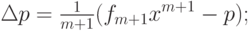
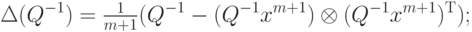( 4)

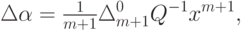
где - ошибка на векторе данных x^{m +1} регрессионной зависимости, полученной на основании выборки .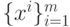

Пересчитывая по приведенным формулам p, Q, Q^-1 и после каждого получения данных, получаем процесс, в котором последовательно уточняются уравнения линейной регрессии. И требуемый объем памяти, и количество операций имеют порядок n² - из-за необходимости накапливать и модифицировать матрицу Q^-1. Конечно, это меньше, чем потребуется на обычное обращение матрицы Q на каждом шаге, однако следующий простой алгоритм еще экономнее. Он вовсе не обращается к матрицам Q, Q^-1 и основан на уменьшении на каждом шаге величины 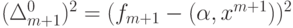- квадрата ошибки на векторе данных x^{m +1} регрессионной зависимости, полученной на основании выборки .

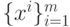Вновь обратимся к формуле (2) и будем рассматривать n +1 -мерные векторы данных и коэффициентов. Обозначим 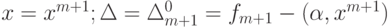. Тогда

( 5)

Последняя элементарная формула столь важна в теории адаптивных сумматоров, что носит "именное название" - формула Уидроу. "Обучение" адаптивного сумматора методом наискорейшего спуска состоит в изменении вектора коэффициентов в направлении антиградиента 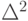: на каждом шаге к добавляется , где h - величина шага.

Если при каждом поступлении нового вектора данных x изменять указанным образом, то получим последовательную процедуру построения линейной аппроксимации функции F(x). Такой алгоритм обучения легко реализуется аппаратными средствами (изменение веса связи 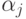есть произведение прошедшего по ней сигнала x_j на ошибку и на величину шага). Возникает, однако, проблема сходимости: если h слишком мало, то сходимость будет медленной, если же слишком велико, то произойдет потеря устойчивости и сходимости не будет вовсе. Детальному изложению этого подхода и его приложений посвящен учебник [2.15].