Основы теории информации и криптографии
[+]
Опубликован: 11.04.2007 | Доступ: свободный | Студентов: 6049 / 2312 | Оценка: 4.37 / 4.24 | Длительность: 11:19:00
Тема: Безопасность
Специальности: Специалист по безопасности
Теги: device controller, DVI, html, LZW, microsoft word, UCS, unix, адаптивного алгоритма, алгоритмы, дискретная случайная величина, код хэмминга, криптография, сжатие, стандарты, таблицей декодирования, телефония, телефоны, теория, теория информации, университеты, форматы, шифрование, шрифты, электронная подпись, элементы
Лекция 6:

Арифметическое кодирование
A
|
версия для печати
< Лекция 5 || Лекция 6: 123 || Лекция 7 >

Адаптивное арифметическое кодирование

Для арифметического кодирования, как и для кодирования методом Хаффмена, существуют адаптивные алгоритмы. Реализация одного из них запатентована фирмой IBM.

Построение арифметического кода для последовательности символов из заданного множества можно реализовать следующим алгоритмом. Каждому символу сопоставляется его вес: вначале он для всех равен 1. Все символы располагаются в естественном порядке, например, по возрастанию. Вероятность каждого символа устанавливается равной его весу, деленному на суммарный вес всех символов. После получения очередного символа и постройки интервала для него, вес этого символа увеличивается на 1 (можно увеличивать вес любым регулярным способом).


Рис. 5.4.

Заданное множество символов - это, как правило, ASCII+. Для того, чтобы обеспечить остановку алгоритма распаковки вначале сжимаемого сообщения надо поставить его длину или ввести дополнительный символ-маркер конца сообщения. Если знать формат файла для сжатия, то вместо начального равномерного распределения весов можно выбрать распределение с учетом этих знаний. Например, в текстовом файле недопустимы ряд управляющих символов и их вес можно занулить.

Пример. Пусть заданное множество - это символы A, B, C. Сжимаемое сообщение - ACCBCAAABC. Введем маркер конца сообщения - E. Кодирование согласно приведенному алгоритму можно провести согласно схеме, приведенной на рис. 5.4.

Вследствие того, что

{759021\over2^{22}=4194304}=0.0010111001010011101101_2\in \Big({9129739\over50450400},{1304249\over7207200}\Big),
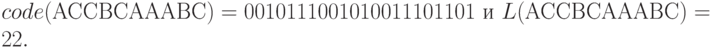
code(\hbox{ACCBCAAABC})=0010111001010011101101\hbox{ и } \ifdim\hsize<150mm {}\fi L(\hbox{ACCBCAAABC})=22.

Поэтому L1(ACCBCAAABC)=2.2 бит/сим. Результат, полученный адаптивным алгоритмом Хаффмена - 4.1 бит/сим, но если кодировать буквы не 8 битами, а 2, то результат будет 2.3 бит/сим. В первой строчке схемы выписаны суммарные веса символов, а во второй - длины текущих отрезков.

Способ распаковки адаптивного арифметического кода почти аналогичен приведенному для неадаптивного. Отличие только в том, что на втором шаге после получения нового кода нужно перестроить разбиение единичного отрезка согласно новому распределению весов символов. Получение маркера конца или заданного началом сообщения числа символов означает окончание работы.

Пример. Распакуем код 0010111001010011101101, зная, что множество символов сообщения состоит из A, B, C и E, причем последний - это маркер конца сообщения.

0.0010111001010011101101_2={759021\over4194304}.

\baselineskip11.7pt \smallskip {\def\dstrut{\setbox1\hbox{ }\dp1=5pt\ht1=11pt\wd1=0pt\box1\relax} \centerline{\vbox{\offinterlineskip\halign{\vrule\ \hfil#\hfil\ & \vrule\ \hfil#\hfil\ &\vrule\ \hfil#\hfil\ & \vrule\ \hfil#\hfil\ &\vrule\ \hfil$#$\hfil\ & \vrule\ \hfil#\hfil\ &\vrule\ \hfil$#$\hfil\ \vrule\cr \noalign{\hrule} \multispan4\strut\vrule\hfil Веса\hfil&&&\hbox{Длина}\cr \multispan4\vrule\hrulefill\vrule& \lowrow{.4}{Число-код и его интервал}& \lowrow{.4}{Символ}&\cr \strut A& B& C& E&&& \hbox{интервала}\cr \noalign{\hrule} \dstrut1& 1& 1& 1& {759021\over4194304}\in(0,{1\over4})& A& {1\over4}\cr \dstrut2& 1& 1& 1& {759021\over1048576}\in({3\over5},{4\over5})& C& {1\over5}\cr \dstrut2& 1& 2& 1& {649377\over1048576}\in({1\over2},{5\over6})& C& {1\over3}\cr \dstrut2& 1& 3& 1& {375267\over1048576}\in({2\over7},{3\over7})& B& {1\over7}\cr \dstrut2& 2& 3& 1& {529717\over1048576}\in({1\over2},{7\over8})& C& {3\over8}\cr \dstrut2& 2& 4& 1& {5429\over393216}\in(0,{2\over9})& A& {2\over9}\cr \dstrut3& 2& 4& 1& {16287\over262144}\in(0,0.3)& A& 0.3\cr \dstrut4& 2& 4& 1& {27145\over131072}\in(0,{4\over11})& A& {4\over11}\cr \dstrut5& 2& 4& 1& {298595\over524288}\in({5\over12},{7\over12})& B& {1\over6}\cr \dstrut5& 3& 4& 1& {240425\over262144}\in({8\over13},{12\over13})& C& {4\over13}\cr \dstrut5& 3& 5& 1& {1028373\over1048576}\in({13\over14},1)& E&\cr \noalign{\hrule}}}.}} \smallskip

Упражнение 29 Составить адаптивный арифметический код с маркером конца для сообщения BAABC.

Дальше >>
< Лекция 5 || Лекция 6: 123 || Лекция 7 >

Вопросы и ответы

вопросов: 1
Сарсен Аяжанов
Сарсен Аяжанов
ответить