|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Пуассоновский процесс
Характеристики Пуассоновского процесса
Фундаментальные свойства Пуассоновского процесса определены в секции 5.2:
а. стационарность;
б. независимость (отсутствие последействия) во все моменты времени (периоды), и
в. простота (ординарность).
(б) и (в) - фундаментальные свойства, тогда как (а) не является необходимым. Таким образом, можно допустить, что Пуассоновский процесс может иметь интенсивность, зависящую от времени поступления. Из этих свойств можно получить другие свойства, которые являются достаточными, чтобы определить Пуассоновский процесс. Два самых важных:
- числовое представление: число событий в пределах временного интервала фиксированной длины имеет Пуассоновское распределение. Поэтому процесс называют Пуассоновским процессом ;
-
представление с помощью интервала: интервал времени
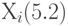 между последовательными событиями является экспоненциально распределенным.
между последовательными событиями является экспоненциально распределенным.
В этом случае, используя (4.8) и (4.10) равенство Феллера- Дженсена (5.4), можно показать фундаментальное отношение между кумулятивным (накопленным) Пуассоновским распределением и распределением Эрланга:
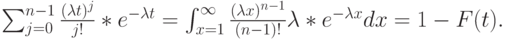 |
( 6.1) |
Эта формула может также быть получена повторным интегрированием по частям.
Распределения Пуассоновского процесса
В этой секции мы поговорим о динамическом и физическом представлении Пуассоновского процесса (1928 [30] и Дженсен, 1954 [11] ). Дифференцирования основаны на простой физической модели и концентрируются на распределениях вероятности, связанных с Пуассоновским процессом.
Физическая модель получается следующим способом. События (поступление) помещены наугад на реальной оси времени независимо от всех других событий, т.е. мы помещаем события однородно и независимо на реальных осях времени.
Средняя плотность выбрана как  события (поступление) в единицу времени. Если рассматривать ось как ось времени, то в среднем мы будем иметь
события (поступление) в единицу времени. Если рассматривать ось как ось времени, то в среднем мы будем иметь  поступлений в единицу времени.
поступлений в единицу времени.
Вероятность, что данное поступление заявки возникает в пределах временного интервала, не зависит от местоположения интервала на оси времени.
В Пуассоновском процессе мы рассматриваем поступление заявки в пределах двух не перекрывающихся временных интервалов продолжительностью 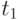 и
и 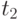 соответственно.
соответственно.
Пусть  обозначают вероятность, что
обозначают вероятность, что  событий возникают в пределах временного интервала продолжительностью
событий возникают в пределах временного интервала продолжительностью  .
.
Математическая формулировка вышеупомянутой модели следующая.
-
Независимость (отсутствие последействия). Если
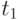 ;и
;и 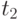 - два не перекрывающихся временных интервала (рис.6.1), мы предполагаем, что они независимы:.
- два не перекрывающихся временных интервала (рис.6.1), мы предполагаем, что они независимы:.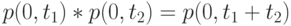
( 6.2) -
Средняя величина временного интервала между двумя последовательными поступлениями заявок -
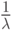 (3.4):
(3.4):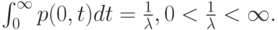
( 6.3) Здесь
 - вероятность, что в пределах временного интервала
- вероятность, что в пределах временного интервала 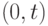 нет поступления заявок. Идентичная вероятность: время, пока произойдет первое событие первое событие, не больше, чем
нет поступления заявок. Идентичная вероятность: время, пока произойдет первое событие первое событие, не больше, чем  (дополнительное распределение). Средняя величина (6.3) получена непосредственно из (3.4). Формула (6.3) может также интерпретироваться как область под кривой
(дополнительное распределение). Средняя величина (6.3) получена непосредственно из (3.4). Формула (6.3) может также интерпретироваться как область под кривой  Это никогда не увеличивающаяся функция, уменьшающаяся от 1 до 0.
Это никогда не увеличивающаяся функция, уменьшающаяся от 1 до 0. -
Отметим, что (6.2) подразумевает, что событие нет поступления заявок в пределах интервала длиной 0 существует и равно:
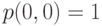
( 6.4) -
Отметим, что (6.3) подразумевает, что вероятность события нет никаких поступлений заявок в пределах интервала времени длиной
 является нулевым и никогда не имеет место
является нулевым и никогда не имеет место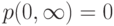
( 6.5)
Экспоненциальное распределение
Следующий существенный шаг в развитии Пуассоновского распределения - получение вероятности 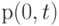 , которая является вероятностью непоступления заявки в пределах временного интервала длины
, которая является вероятностью непоступления заявки в пределах временного интервала длины  , то есть вероятности, что первое поступление заявки произойдет позже, чем
, то есть вероятности, что первое поступление заявки произойдет позже, чем  . Мы покажем, что
. Мы покажем, что  - экспоненциальное распределение (сравните с результатом секции 4.1).
- экспоненциальное распределение (сравните с результатом секции 4.1).
Из (6.2) мы имеем:
 |
( 6.6) |
Обозначая  , (6.6) может быть записано как:
, (6.6) может быть записано как:
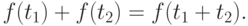 |
( 6.7) |
Дифференцируя, например, по 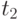 , мы имеем
, мы имеем
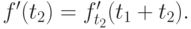
Заметим, что 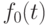 должна быть константой, и поэтому
должна быть константой, и поэтому
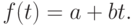 |
( 6.8) |
Подставляя (6.8) в (6.7), мы получаем 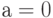 . Тогда
. Тогда  имеет форму
имеет форму

Из (6.3) мы получаем 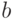 :
:
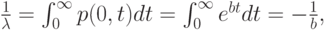
или
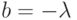
Таким образом, на основе пункта (1) и (2) выше мы показали, что:
 |
( 6.9) |
Если мы рассматриваем  как вероятность того, что следующее событие наступает позже, чем за время
как вероятность того, что следующее событие наступает позже, чем за время  , тогда время до следующего прибытия является экспоненциально распределенным (секция. 4.1):
, тогда время до следующего прибытия является экспоненциально распределенным (секция. 4.1):
 |
( 6.10) |
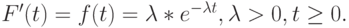 |
( 6.11) |
Мы имеем следующую среднюю величину и дисперсию (4.4):
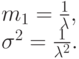 |
( 6.12) |
Вероятность, что следующее появление заявки в пределах интервала 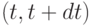 может быть записана, как:
может быть записана, как:
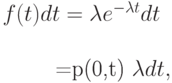 |
( 6.13) |
то есть вероятность, что заявка поступит в пределах интервала 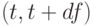 , равна
, равна 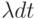 , независимо om
, независимо om  пропорционально
пропорционально 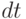 (3.17).
(3.17).
Поскольку  независима от величины ( возраста )
независима от величины ( возраста )  , экспоненциальное распределение не имеет памяти (сравните секции 4.1 и 3.1.2). Процесс не имеет возраста.
, экспоненциальное распределение не имеет памяти (сравните секции 4.1 и 3.1.2). Процесс не имеет возраста.
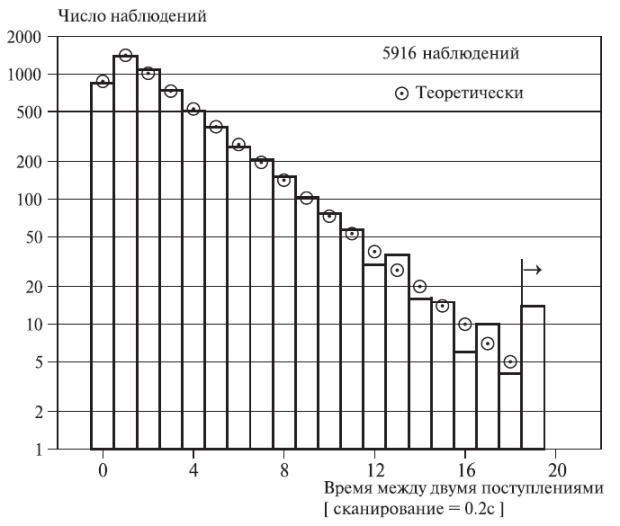
Параметр  называется интенсивностью или скоростью экспоненциального распределения и соответствующего Пуассоновского процесса, и это соответствует интенсивности в (5.6). Экспоненциальное распределение - вообще очень хорошая модель для интервалов поступления вызовов, когда нагрузка генерируется автоматически, а не вручную (рис.6.2).
называется интенсивностью или скоростью экспоненциального распределения и соответствующего Пуассоновского процесса, и это соответствует интенсивности в (5.6). Экспоненциальное распределение - вообще очень хорошая модель для интервалов поступления вызовов, когда нагрузка генерируется автоматически, а не вручную (рис.6.2).
Теоретические значения получены при условии экспоненциально распределенных времен интервалов. Согласно принципу измерения (метод сканирования) непрерывное экспоненциальное распределение преобразовано в дискретное распределение Вестберга (Westerberg) (15.14) (критерий -  = 18,86 с 19 степенями свободы, квантиль = 53)
= 18,86 с 19 степенями свободы, квантиль = 53)
Распределение Эрланга k-ого порядка
Из приведенного выше можно заметить, что время поступления точно  событий определяется суммой
событий определяется суммой  IID (independently and identically distributed - независимо и тождественно распределенных) экспоненциально распределенных случайных переменных.
IID (independently and identically distributed - независимо и тождественно распределенных) экспоненциально распределенных случайных переменных.
Распределение этой суммы - распределение Эрланга k - ого порядка (секция 4.2), и плотность равна:
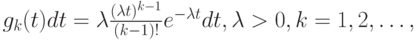 |
( 6.14) |
Для 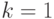 мы получаем экспоненциальное распределение. Распределение
мы получаем экспоненциальное распределение. Распределение  , получено свертыванием
, получено свертыванием  и
и 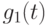 . Если мы принимаем, что выражение (6.14) правильно для
. Если мы принимаем, что выражение (6.14) правильно для 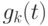 , тогда получаем свертыванием:
, тогда получаем свертыванием:
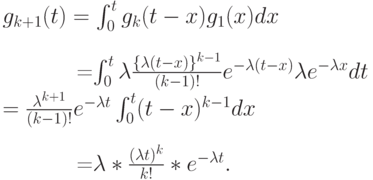
Так как выражение справедливо при 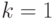 , согласно приведенной выше индукции мы имеем, что это справедливо для любого
, согласно приведенной выше индукции мы имеем, что это справедливо для любого  .
.
Распределение Эрланга  -ого порядка со статистической точки зрения - это специальное гамма-распределение.
-ого порядка со статистической точки зрения - это специальное гамма-распределение.
Средняя величина и дисперсия получаются из (6.12):
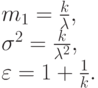 |
( 6.15) |
Пример 6.2.1: статистика вызова в системе с программным управлением (сравните с Примером 5.1.2)
Пусть вызовы поступают в систему с программным управлением, например, на программно управляемую телефонную станцию ( SPC - System Program Control ), согласно Пуассоновскому процессу. Станция автоматически собирает полную информацию о каждом 1000-ном вызове. Интервалы поступления между двумя регистрацией тогда будут иметь 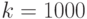 распределение Эрланга и иметь коэффициент формы
распределение Эрланга и иметь коэффициент формы 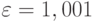 , то есть регистрация будет очень регулярной.
, то есть регистрация будет очень регулярной.
Пуассоновское распределение
Покажем теперь, что число поступления заявок в интервал фиксированной длины  имеет Пуассоновское распределение со средней величиной
имеет Пуассоновское распределение со средней величиной 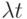 . Когда мы знаем вышеупомянутое экспоненциальное распределение и распределение Эрланга, дифференцирование Пуассоновского распределения - только вопрос применения простой комбинаторики. Доказательство может быть осуществлено по индукции.
. Когда мы знаем вышеупомянутое экспоненциальное распределение и распределение Эрланга, дифференцирование Пуассоновского распределения - только вопрос применения простой комбинаторики. Доказательство может быть осуществлено по индукции.
Мы хотим получить 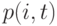 = вероятность
= вероятность 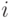 -ого поступления заявки в пределах временного интервала t. Предположим, что:
-ого поступления заявки в пределах временного интервала t. Предположим, что:
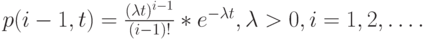
Это справедливо, для  . Интервал (0, t) разделен на три не перекрывающихся интервала:
. Интервал (0, t) разделен на три не перекрывающихся интервала: 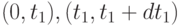 и
и 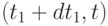 . Из предположения о независимости мы знаем, что события в пределах интервала не зависят от событий в других интервалах, потому что интервалы - не перекрывающиеся. Выбирая
. Из предположения о независимости мы знаем, что события в пределах интервала не зависят от событий в других интервалах, потому что интервалы - не перекрывающиеся. Выбирая 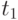 так, чтобы последнее поступление заявки в пределах
так, чтобы последнее поступление заявки в пределах 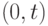 появлялось в интервале
появлялось в интервале  , получим вероятность
, получим вероятность  объединением по всем возможным значениям t как произведение следующих трех вероятностей.
объединением по всем возможным значениям t как произведение следующих трех вероятностей.
-
Вероятность, что
 поступление произойдет в пределах временного интервала
поступление произойдет в пределах временного интервала 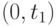 :
: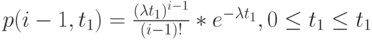 .
. -
Вероятность, что только одно поступление произойдет в пределах временного интервала от
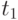 до
до 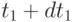
 .
. -
Вероятность, что не произойдет поступление в пределах временного интервала от
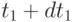 до
до 
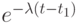 .
.
Произведение первых двух вероятностей дает вероятность того, что 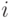 -тая заявка поступит в момент
-тая заявка поступит в момент 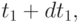 т.е. будет иметь место Эрланговское распределение из предыдущей секции.
т.е. будет иметь место Эрланговское распределение из предыдущей секции.
Интегрируя, мы получаем
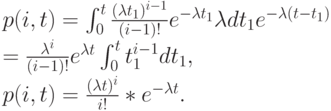 |
( 6.16) |
Это - Пуасоновское распределение, которое мы, таким образом, получили из (6.9) индукцией. Средняя величина и дисперсия:
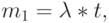 |
( 6.17) |
 |
( 6.18) |
Пуассоновское распределение - очень хорошая модель для числа вызовов в телекоммуникационной системе (рис.6.3) или вакантных мест в компьютерной системе.