Методы дедуктивных и индуктивных рассуждений
Аннушка... Аннушка?.. – забормотал поэт, тревожно озираясь, - позвольте, позвольте...
К слову "Аннушка" привязались слова "подсолнечное масло", а затем почему-то "Понтий Пилат". Пилата поэт отринул и стал вязать цепочку, начиная со слова "Аннушка". И цепочка эта связалась очень быстро и тотчас привела к сумасшедшему профессору.
М.А. Булгаков. "Мастер и Маргарита"
Возможности автоматизации достоверных (дедуктивных) рассуждений
Если у тебя спрошено будет, что полезнее, солнце или месяц? – ответствуй: месяц. Ибо солнце светит днём, когда и без того светло; а месяц – ночью.
Козьма Прутков
Опишем общую схему выводов, лежащих в основе большого количества моделей человеческих достоверных (дедуктивных) рассуждений.
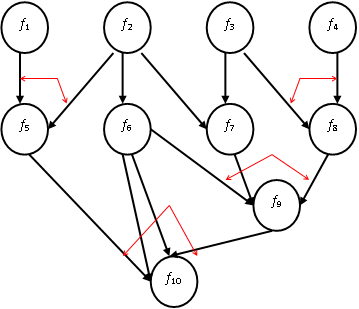
На рис. 4.1 показано некоторое дерево вывода истинности утверждения f10.
Первый ярус дерева образуют вершины f1, f2, f3, f4, выполняющие роль аксиом, или утверждений, истинность которых задаётся извне. Стрелки сходятся в одной точке (например,  и
и  ), если значение ИСТИНА второго высказывания, достигается при значении ИСТИНА всех первых высказываний (т.е. по схеме И). Стрелки входят в разные точки, если значение ИСТИНА имеет хотя бы одно "входящее" высказывание (если обусловленные ими связи действуют по схеме ИЛИ). Во избежание коллизии стрелки могут дублироваться (две стрелки
), если значение ИСТИНА второго высказывания, достигается при значении ИСТИНА всех первых высказываний (т.е. по схеме И). Стрелки входят в разные точки, если значение ИСТИНА имеет хотя бы одно "входящее" высказывание (если обусловленные ими связи действуют по схеме ИЛИ). Во избежание коллизии стрелки могут дублироваться (две стрелки  ), а стрелки, обозначающие дизъюнкцию, соединяются скобкой (стрелки
), а стрелки, обозначающие дизъюнкцию, соединяются скобкой (стрелки  и
и  и
и  и др.).
и др.).
Таким образом, возможны разные пути доказательства любого промежуточного и конечного утверждения. Например, доказательство утверждения f9 возможно двумя путями. Раз доказаны утверждения f2 и f3, то f7 следует из их доказанности. Утверждение f6 следует из доказанности f2, тогда f9 следует из доказанности f6 и f7. Второй путь доказательства f9 следует из доказательства f8 на основе f2 или f4.
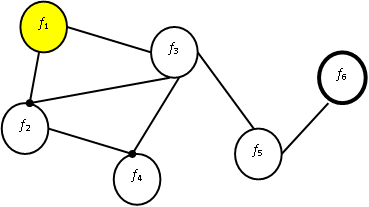
Схема вывода не обязательно описывается в виде дерева. Она может иметь вид произвольной ориентированной или неориентированной сети (рис. 4.2). "Жирная" точка означает, что, например, для доказательства f2 необходимо доказательство как f2, так и f4. Такая логическая сеть называется И-ИЛИ сетью.
Пусть требуется доказать утверждение f6 (на рисунке этому соответствует отмеченная целевая вершина). Априорно доказано утверждение f1. Как из f1 получить f6? Если все связи допускают любую ориентацию, то из f1 можно получить f3, затем f5 и, наконец, f6.
Мы сразу нашли решение, потому что видим его. Но как построить алгоритм перебора возможных смещений в лабиринте возможностей для доказательства пути в целевую вершину?
В данном случае, перебирая возможности смещения из f1, мы пытаемся вывести утверждение f2, но этого нельзя сделать, т.к. требуется доказательство утверждения f3. Обнаруживаем, что доказательство возможно. Теперь доказаны f1 и f3. Попытка продвинуться в f2 и f5 оказывается успешной. На следующем шаге доказываются утверждения f4 и f6. После "чистки" ненужных выводов, остаётся реальный кратчайший путь доказательства  .
.
Возможен и другой путь доказательства – метод обратной волны (аналог метода динамического программирования). Чтобы доказать f6, надо доказать f5; чтобы доказать f5, надо доказать f3; следует воспользоваться начальным утверждением f1.
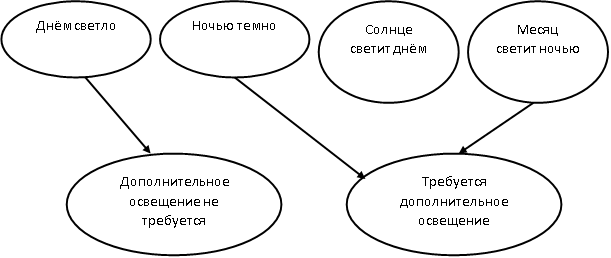
Рассмотрим блестящее умозаключение Козьмы Пруткова, рекомендуемое в эпиграфе. Дерево вывода изображено на рис. 4.3. На первом ярусе отражены исходные посылки – аксиомы, обладающие (с точки зрения К. Пруткова) значениями ИСТИНА.
Как видим, солнышку вообще делать нечего, что вполне в духе софистических рассуждений.
Известны схемы вывода альтернативные деревья, альтернативные сети и другие аналоги метода "ветвей и границ".
В рамках данного раздела совершим неформальный переход к нечётким данным, концепция которых уже легла в основу разработки математической логики событий. Будем оперировать высказываниями, значение ИСТИНА которых определена с некоторой вероятностью, как было рассмотрено в Лекции 1.
Рассмотрим пример расчёта надёжности управляющего компьютера, как вероятности решения своей задачи в цикле управления длительности t.
увеличить изображение
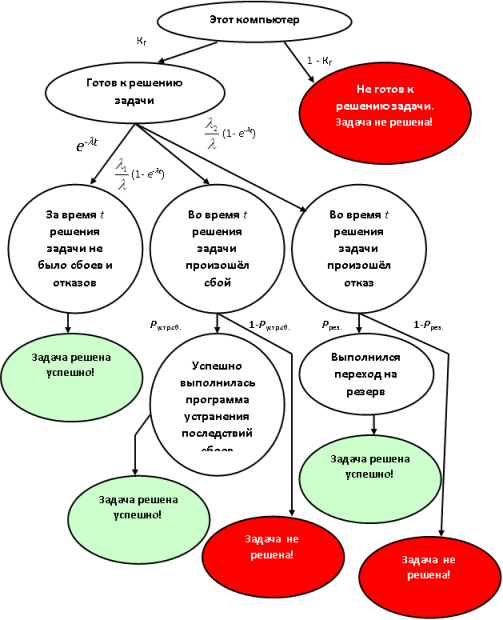
Рис. 4.4. Вероятностное дерево логических возможностей для расчёта надёжности компьютера
На рис. 4.4 представлено вероятностное дерево логических возможностей, отражающее многие пути следования к обоснованию положительной ситуации – успешного решения задачи. Мы видим, что дерево вывода как бы перевёрнуто и обладает не единственной целевой вершиной. Принятые обозначения и формулы:
КГ – коэффициент готовности, находится из отношения

, где Т0 - среднее время безотказной работы, Твосст – среднее время восстановления оборудования при неисправности; 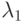 – частота сбоев,
– частота сбоев, 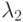 – частота отказов,
– частота отказов, 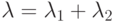 ; Рустр.сб. – вероятность успешного устранения последствий сбоев во время решения задачи; Ррез. – вероятность успешного перехода на резерв во время решения задачи.
; Рустр.сб. – вероятность успешного устранения последствий сбоев во время решения задачи; Ррез. – вероятность успешного перехода на резерв во время решения задачи.
Тогда надёжность Р находится как сумма произведений условных вероятностей по всем ветвям дерева, ведущим к успеху:
 |
( 4.1) |