|
Здравствуйте! Записался на ваш курс, но не понимаю как произвести оплату. Надо ли писать заявление и, если да, то куда отправлять? как я получу диплом о профессиональной переподготовке? |
Планирование процессов
Shortest-Job-First (SJF)
При рассмотрении алгоритмов FCFS и RR мы видели, насколько существенным для них является порядок расположения процессов в очереди процессов, готовых к исполнению. Если короткие задачи расположены в очереди ближе к ее началу, то общая производительность этих алгоритмов значительно возрастает. Если бы мы знали время следующих CPU burst для процессов, находящихся в состоянии готовность, то могли бы выбрать для исполнения не процесс из начала очереди, а процесс с минимальной длительностью CPU burst. Если же таких процессов два или больше, то для выбора одного из них можно использовать уже известный нам алгоритм FCFS. Квантование времени при этом не применяется. Описанный алгоритм получил название "кратчайшая работа первой" или Shortest Job First ( SJF ).
SJF-алгоритм краткосрочного планирования может быть как вытесняющим, так и невытесняющим. При невытесняющем SJF - планировании процессор предоставляется избранному процессу на все необходимое ему время, независимо от событий, происходящих в вычислительной системе. При вытесняющем SJF - планировании учитывается появление новых процессов в очереди готовых к исполнению (из числа вновь родившихся или разблокированных) во время работы выбранного процесса. Если CPU burst нового процесса меньше, чем остаток CPU burst у исполняющегося, то исполняющийся процесс вытесняется новым.
Рассмотрим пример работы невытесняющего алгоритма SJF. Пусть в состоянии готовность находятся четыре процесса, p0, p1, p2 и p3, для которых известны времена их очередных CPU burst. Эти времена приведены в таблице 3.4. Как и прежде, будем полагать, что вся деятельность процессов ограничивается использованием только одного промежутка CPU burst, что процессы не совершают операций ввода-вывода и что временем переключения контекста можно пренебречь.
При использовании невытесняющего алгоритма SJF первым для исполнения будет выбран процесс p3, имеющий наименьшее значение продолжительности очередного CPU burst. После его завершения для исполнения выбирается процесс p1, затем p0 и, наконец, p2. Эта картина отражена в таблице 3.5.
| Время | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p0 | Г | Г | Г | Г | И | И | И | И | И | |||||||
| p1 | Г | И | И | И | ||||||||||||
| p2 | Г | Г | Г | Г | Г | Г | Г | Г | Г | И | И | И | И | И | И | И |
| p3 | И |
Как мы видим, среднее время ожидания для алгоритма SJF составляет (4 + 1 + 9 + 0)/4 = 3,5 единицы времени. Легко посчитать, что для алгоритма FCFS при порядке процессов p0, p1, p2, p3 эта величина будет равняться (0 + 5 + 8 + 15)/4 = 7 единицам времени, т. е. будет в два раза больше, чем для алгоритма SJF. Можно показать, что для заданного набора процессов (если в очереди не появляются новые процессы) алгоритм SJF является оптимальным с точки зрения минимизации среднего времени ожидания среди класса невытесняющих алгоритмов.
Для рассмотрения примера вытесняющего SJF планирования мы возьмем ряд процессов p0, p1, p2 и p3 с различными временами CPU burst и различными моментами их появления в очереди процессов, готовых к исполнению (см. табл. 3.6.).
| Процесс | Время появления в очереди очередного CPU burst | Продолжительность |
|---|---|---|
| p0 | 0 | 6 |
| p1 | 2 | 2 |
| p2 | 6 | 7 |
| p3 | 0 | 5 |
В начальный момент времени в состоянии готовность находятся только два процесса, p0 и p3. Меньшее время очередного CPU burst оказывается у процесса p3, поэтому он и выбирается для исполнения (см. таблицу 3.7.). По прошествии 2 единиц времени в систему поступает процесс p1. Время его CPU burst меньше, чем остаток CPU burst у процесса p3, который вытесняется из состояния исполнение и переводится в состояние готовность. По прошествии еще 2 единиц времени процесс p1 завершается, и для исполнения вновь выбирается процесс p3. В момент времени t = 6 в очереди процессов, готовых к исполнению, появляется процесс p2, но поскольку ему для работы нужно 7 единиц времени, а процессу p3 осталось трудиться всего 1 единицу времени, то процесс p3 остается в состоянии исполнение. После его завершения в момент времени t = 7 в очереди находятся процессы p0 и p2, из которых выбирается процесс p0. Наконец, последним получит возможность выполняться процесс p2.
| Время | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p0 | Г | Г | Г | Г | Г | Г | Г | И | И | И | И | И | И | |||||||
| p1 | И | И | ||||||||||||||||||
| p2 | Г | Г | Г | Г | Г | Г | Г | И | И | И | И | И | И | И | ||||||
| p3 | И | И | Г | Г | И | И | И |
Основную сложность при реализации алгоритма SJF представляет невозможность точного знания продолжительности очередного CPU burst для исполняющихся процессов. В пакетных системах количество процессорного времени, необходимое заданию для выполнения, указывает пользователь при формировании задания. Мы можем брать эту величину для осуществления долгосрочного SJF - планирования. Если пользователь укажет больше времени, чем ему нужно, он будет ждать результата дольше, чем мог бы, так как задание будет загружено в систему позже. Если же он укажет меньшее количество времени, задача может не досчитаться до конца. Таким образом, в пакетных системах решение задачи оценки времени использования процессора перекладывается на плечи пользователя. При краткосрочном планировании мы можем делать только прогноз длительности следующего CPU burst, исходя из предыстории работы процесса. Пусть 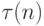 – величина n -го CPU burst, T(n + 1) – предсказываемое значение для n + 1 -го CPU burst,
– величина n -го CPU burst, T(n + 1) – предсказываемое значение для n + 1 -го CPU burst,  – некоторая величина в диапазоне от 0 до 1.
– некоторая величина в диапазоне от 0 до 1.
Определим рекуррентное соотношение
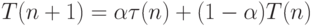
T(0) положим произвольной константой. Первое слагаемое учитывает последнее поведение процесса, тогда как второе слагаемое учитывает его предысторию. При 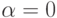 мы перестаем следить за последним поведением процесса, фактически полагая
мы перестаем следить за последним поведением процесса, фактически полагая
T(n)= T(n+1)=...=T(0)
т. е. оценивая все CPU burst одинаково, исходя из некоторого начального предположения.
Положив 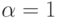 , мы забываем о предыстории процесса. В этом случае мы полагаем, что время очередного CPU burst будет совпадать со временем последнего CPU burst:
, мы забываем о предыстории процесса. В этом случае мы полагаем, что время очередного CPU burst будет совпадать со временем последнего CPU burst:
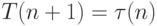
Обычно выбирают 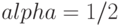 для равноценного учета последнего поведения и предыстории. Надо отметить, что такой выбор
для равноценного учета последнего поведения и предыстории. Надо отметить, что такой выбор  удобен и для быстрой организации вычисления оценки T(n + 1). Для подсчета новой оценки нужно взять старую оценку, сложить с измеренным временем CPU burst и полученную сумму разделить на 2, например, сдвинув ее на 1 бит вправо. Полученные оценки T(n + 1) применяются как продолжительности очередных промежутков времени непрерывного использования процессора для краткосрочного SJF - планирования.
удобен и для быстрой организации вычисления оценки T(n + 1). Для подсчета новой оценки нужно взять старую оценку, сложить с измеренным временем CPU burst и полученную сумму разделить на 2, например, сдвинув ее на 1 бит вправо. Полученные оценки T(n + 1) применяются как продолжительности очередных промежутков времени непрерывного использования процессора для краткосрочного SJF - планирования.
