|
Подскажите, пожалуйста, планируете ли вы возобновление программ высшего образования? Если да, есть ли какие-то примерные сроки? Спасибо! |
Признаковые распознающие нейронные сети
Современные признаковые распознающие нейронные сети (ПРНС), так же как и растровые нейронные распознаватели, можно считать развитием перцептрона Ф. Розенблатта. Часто между ними вообще не делают различия, называя перцептроном любой распознаватель, построенный с использованием формальных нейронов. Будем проводить условную границу между перцептроном и ПРНС, называя перцептроном растровый распознаватель, а ПРНС - признаковый. (С оговоркой, что фиксированное множество независимых двоичных признаков фактически является растром.) Можно считать, что предпринятая Розенблаттом попытка получить обобщения и эффективное распознавание изображений в формальной нейронной сети с растровым входом без предварительных преобразований входной информации не удалась. Это послужило толчком к развитию признаковых нейронных распознавателей, в том числе и распознавателей, работающих с много градационными зависимыми признаками.
Необходимость или по крайней мере целесообразность изменения модели Розенблатта путем перехода от задач распознавания растровых изображений к задачам распознавания по признакам была понятна многим исследователям. При разработке перцептрона первичная цель состояла в том, чтобы понять, как работает мозг в процессе распознавания зрительных образов, спроектированных на входной растр зрительного анализатора. При создании ПРНС на первое место вышла практическая цель - распознавание.
Формальную распознающую нейронную сеть часто рассматривают как черный ящик, имеющий вход, выход и какое-то почти таинственное, строго не определяемое внутреннее функционирование. Попробуем настолько, насколько это возможно, заглянуть внутрь черного ящика.
Распознавание с помощью разделяющих гиперплоскостей
Итак, на вход ПРНС подается не поточечный растр, а в общем случае многоградационные признаки, причем признаки любой модальности, то есть распознаваться, как и в любой признаковой распознающей системе, могут не только изображения, а все что угодно, например, звуки, болезни по их симптомам, геологические объекты и так далее. Поэтому в публикациях часто приводят очень широкие списки областей применения ПРНС. При этом нужно понимать, что широта области применения относится не к распознающим нейронным сетям, а к распознаванию по признакам. Одна область применения отличается от другой не какой-то принципиальной спецификой работы нейронной сети, а в первую очередь алфавитом, особенностями и способом получения используемых для распознавания признаков.
Что касается живого мозга, информация в зрительный анализатор коры головного мозга передается и как растровая проекция, и как признаки. Первичное получение простейших зрительных признаков происходит в рецептивных полях - связанных с сетчаткой глаза специальных нейронных сетях. Кроме того, зрительный анализатор мозга устроен, по-видимому, иерархически с последовательным усложнением анализируемых признаков. Проблема получения признаков, тем более формирования их иерархии, в современных распознающих нейронных сетях обычно не рассматривается.
Формальный нейрон - это пороговый элемент, который имеет число входов, равное числу участвующих в распознавании признаков, и один выход. Признаки на входах могут иметь много градаций. Каждая входная связь имеет свой вес. Веса связей могут быть как положительными, так и отрицательными. Классический формальный нейрон считает взвешенную алгебраическую сумму значений входных признаков и сравнивает ее с фиксированным порогом. Если эта сумма меньше порога, то выход нейрона равен -1, если больше порога, то +1. Это иллюстрирует сплошная линия на рис. 12.1.
Условие срабатывания нейрона:
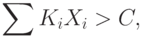
 - весовой коэффициент,
- весовой коэффициент,
 - порог срабатывания. Величины признаков и коэффициентов могут иметь как положительные, так и отрицательные значения. Уравнение срабатывания нейрона с заменой знака > на знак = определяет гиперплоскость в пространстве признаков (при двух признаках - прямую линию).
- порог срабатывания. Величины признаков и коэффициентов могут иметь как положительные, так и отрицательные значения. Уравнение срабатывания нейрона с заменой знака > на знак = определяет гиперплоскость в пространстве признаков (при двух признаках - прямую линию).
Каждому распознаваемому объекту соответствует вектор в пространстве признаков. В соответствии с уравнением срабатывания нейрон строит гиперплоскость в пространстве признаков и определяет, по какую сторону от этой плоскости лежит точка, соответствующая вектору признаков распознаваемого объекта. Как проходит гиперплоскость, зависит от коэффициентов  и порога
и порога  .
.
Часто, рассматривая условие срабатывания нейрона, забывают о том, что формальный нейрон просто строит разделяющую гиперплоскость в пространстве признаков, и говорят о весе  -ro признака, о вкладе признака в сумму
-ro признака, о вкладе признака в сумму  , о различной значимости признаков в зависимости от их веса и тому подобное. По-видимому, может вводить в заблуждение термин "вес признака". В действительности
, о различной значимости признаков в зависимости от их веса и тому подобное. По-видимому, может вводить в заблуждение термин "вес признака". В действительности  - это не вес, а просто коэффициент в уравнении разделяющей гиперплоскости, определяющий ее положение в пространстве признаков.
- это не вес, а просто коэффициент в уравнении разделяющей гиперплоскости, определяющий ее положение в пространстве признаков.
Для распознавания объектов, относящихся к двум классам, может оказаться достаточным один нейрон. Это возможно в случае, когда в пространстве признаков существует такая гиперплоскость, что все точки, соответствующие векторам признаков объектов первого класса, лежат по одну сторону от этой гиперплоскости, а все точки, отображающие объекты второго класса, - по другую. Этот случай иллюстрирует рис. 12.2-а.
Качественно определить подобный случай можно следующим образом: точки, отображающие объекты каждого класса в пространстве признаков, расположены компактно, поверхности, огибающие множество точек каждого класса, допускают выпуклые не пересекающиеся аппроксимации.
Задача построения разделяющей гиперплоскости состоит в определении коэффициентов  и порога
и порога  . Решается эта задача при обучении с использованием большого числа примеров - обучающих выборок. Поскольку при обучении могут использоваться только конечные обучающие выборки, даже в простом случае, подобном приведенному выше,
. Решается эта задача при обучении с использованием большого числа примеров - обучающих выборок. Поскольку при обучении могут использоваться только конечные обучающие выборки, даже в простом случае, подобном приведенному выше,
решается не задача абсолютного разделения, а лишь задача максимизации вероятности правильного отнесения неизвестного распознаваемого объекта к одному из классов, или, что то же самое, задача минимизации вероятности ошибки. Эта задача решается не строго и тем лучше, чем представительней обучающая выборка и чем выше ее статистическая достоверность.
Проведение разделяющей гиперплоскости, то есть нахождение необходимых для наилучшего разделения классов параметров  и
и  нейрона, усложняется, если поверхности, огибающие множество точек каждого класса, пересекаются. Такой случай показан на рис. 12.2-b.
нейрона, усложняется, если поверхности, огибающие множество точек каждого класса, пересекаются. Такой случай показан на рис. 12.2-b.
Как видно из иллюстрируемого рисунком примера, провести разделяющую плоскость так, чтобы точки, представляющие в обучающей выборке объекты первого класса, лежали по одну сторону от плоскости, а второго класса - по другую, в этом случае невозможно.
Тем не менее задача решается эвристически с использованием по-прежнему только одного нейрона. При этом при нахождении величин  и
и  можно строить целевую функцию, вычисляемую на всех точках обучающей выборки и зависящую, например, от числа ошибок на обучающей выборке либо от каких-то функций расстояний от точек обучающей выборки до разделяющей плоскости.
можно строить целевую функцию, вычисляемую на всех точках обучающей выборки и зависящую, например, от числа ошибок на обучающей выборке либо от каких-то функций расстояний от точек обучающей выборки до разделяющей плоскости.
Еще усложним задачу. Рис. 12.2-е иллюстрирует случай, когда поверхности, огибающие множество точек обучающей выборки каждого из двух распознаваемых классов, не выпуклы и расположены так, что проведение разделяющей плоскости невозможно. Однако в этом случае существует разделяющая поверхность, которую можно попытаться аппроксимировать плоскостями. Для аппроксимации нелинейной разделяющей поверхности с использованием нейронов нужно несколько нейронов, по числу аппроксимирующих плоскостей.
Предположим, что для обучающей выборки, состоящей по-прежнему из объектов только двух классов и "невыпуклого" случая, иллюстрируемого рис. 12.2-е, удалось при обучении получить значения  и
и 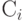 для всех аппроксимирующих гиперплоскостей (нейронов). Назовем эти нейроны нейронами первого уровня. Теперь для получения результата распознавания необходим еще один - второй уровень, объединяющий результаты первого уровня. В случае распознавания объектов двух классов этот уровень должен состоять из одного нейрона, выход которого (+1 или - 1) указывает, к какому из двух классов относится распознаваемый объект. Нейрон второго выходного уровня строит разделяющую плоскость в пространстве значений выходов нейронов первого уровня.
для всех аппроксимирующих гиперплоскостей (нейронов). Назовем эти нейроны нейронами первого уровня. Теперь для получения результата распознавания необходим еще один - второй уровень, объединяющий результаты первого уровня. В случае распознавания объектов двух классов этот уровень должен состоять из одного нейрона, выход которого (+1 или - 1) указывает, к какому из двух классов относится распознаваемый объект. Нейрон второго выходного уровня строит разделяющую плоскость в пространстве значений выходов нейронов первого уровня.
На втором нейронном уровне могут возникнуть проблемы, связанные с необходимостью реализации в некоторых случаях "исключающего ИЛИ". Снять эту проблему можно обычным программным путем либо путем предшествующей обучению кластеризации обучающего множества. При этом число распознаваемых на первом нейронном уровне классов увеличивается на число дополнительно вводимых кластеров.
Классический формальный нейрон, реализуя приведенное уравнение срабатывания, строит разделяющую плоскость в  -мерном пространстве признаков (при
-мерном пространстве признаков (при 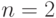 - прямую линию). Уйти от необходимости аппроксимировать плоскостями нелинейную разделяющую поверхность и вводить дополнительный результирующий или собирающий нейронный слой можно, изменив уравнение нейрона. Например, нейрон может строить не уравнение гиперплоскости, а уравнение
- прямую линию). Уйти от необходимости аппроксимировать плоскостями нелинейную разделяющую поверхность и вводить дополнительный результирующий или собирающий нейронный слой можно, изменив уравнение нейрона. Например, нейрон может строить не уравнение гиперплоскости, а уравнение  -мерного эллипсоида (на плоскости - эллипса),
то есть считать взвешенную сумму квадратов значений признаков. На формальном нейроне, имеющем
-мерного эллипсоида (на плоскости - эллипса),
то есть считать взвешенную сумму квадратов значений признаков. На формальном нейроне, имеющем  входов, меняя уравнение срабатывания можно строить любую разделяющую поверхность, определяемую любой вычислимой функцией
входов, меняя уравнение срабатывания можно строить любую разделяющую поверхность, определяемую любой вычислимой функцией  переменных. Правда, в этом случае может значительно усложниться задача обучения, т. е. построения уравнений разделяющих поверхностей, и усилиться сомнение в правомочности использования слова "нейрон".
переменных. Правда, в этом случае может значительно усложниться задача обучения, т. е. построения уравнений разделяющих поверхностей, и усилиться сомнение в правомочности использования слова "нейрон".
До сих пор мы рассматривали задачу распознавания объектов, относящихся к двум классам. Задача распознавания в случае, когда число классов больше двух, например,  сводится к
сводится к  задачам с двумя классами. В каждой из этих
задачам с двумя классами. В каждой из этих  задач должна рассматриваться задача распознавания с двумя классами, когда первый класс - это один из
задач должна рассматриваться задача распознавания с двумя классами, когда первый класс - это один из  классов основной решаемой задачи распознавания, а второй класс - это объединение всех остальных
классов основной решаемой задачи распознавания, а второй класс - это объединение всех остальных 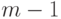 классов.
классов.
В рамках приведенной выше логики с использованием в явном виде разделяющих гиперплоскостей в пространстве признаков можно строить распознающие системы, не апеллируя к нейронам и нейронным сетям. Особенно просто и естественно это делать при распознавании двух классов объектов. Именно так организован и работает дифференциальный уровень системы распознавания символов печатного текста - FineReader, а также дифференциальные уровни систем распознавания рукописных текстов FineReader -рукопись и FormReader. На этих уровнях распознавателей текстов при обучении отыскиваются аналитические зависимости, задающие разделяющие гиперплоскости в пространстве признаков. Это же можно реализовать и на формальных нейронах. При этом в распознавании ровным счетом ничего не изменится.
Отметим, что, работая с разделяющими гиперплоскостями, или, что то же самое, с формальными нейронами, нужно иметь в виду, что мерность пространства признаков должна быть фиксирована и не меняться как при обучении, так и при распознавании разных объектов. Например, нельзя, построив при обучении разделяющую плоскость в трехмерном пространстве признаков, уменьшить мерность пространства признаков и пытаться распознавать, используя не плоскость, а разделяющую прямую линию. В связи с этим может возникать определенная проблема, поскольку отдельные признаки могут быть разрушены и не вычислимы на конкретных объектах распознавания. При обучении такие случаи должны идентифицироваться, а такие объекты можно попросту пропускать. При распознавании такие объекты тоже, конечно, можно пропускать, то есть не распознавать этим методом. Но можно и пытаться их распознавать, выполняя с целью сохранения мерности разделяющей гиперплоскости определенные специальные действия для замещения отсутствующих признаков некоторыми фиктивными "безвредными" значениями.
На рис. 12.1 сплошной линией показана выходная характеристика классического формального нейрона. В современных ПРНС обычно используются нейроны, у которых пороговый скачок от -1 к +1 заменяется плавным дифференцируемым, чаще всего сигмаобразным переходом, показанным на рис. 12.1 пунктиром.
Такой нейрон по-прежнему строит разделяющую гиперплоскость. Во всех точках пространства признаков, лежащих по одну сторону от разделяющей плоскости, выход нейрона равен положительной величине, по другую сторону - отрицательной.
Введение в формальном нейроне вместо порогового скачка плавного дифференцируемого перехода ничего принципиально в распознавании не меняет, а лишь позволяет использовать различные градиентные алгоритмы обучения сети, то есть алгоритмы нахождения коэффициентов в уравнениях разделяющих гиперплоскостей. Кроме того, плавная выходная характеристика нейрона дает возможность получать оценку уверенности распознающей системы в результате распознавания. Эта оценка используется в некоторых системах распознавания при формировании результата. В то же время нужно понимать, что эта оценка, строго говоря, не является ни вероятностью правильного распознавания, ни расстоянием до разделяющей гиперплоскости. Правда, ни из чего не следует, что евклидово расстояние до разделяющей гиперплоскости в пространстве признаков всегда является наилучшим или просто хорошим критерием для получения количественной оценки "уверенности" системы в правильности результата распознавания. Не исключено, что в каких-то конкретных случаях строить разделяющие поверхности в пространстве признаков и определять в этом пространстве расстояния лучше в какой-нибудь другой метрике.
Существующие многочисленные варианты признаковых распознающих нейронных сетей в подавляющем большинстве случаев принципиально отличаются друг от друга только используемыми градиентными алгоритмами обучения, то есть алгоритмами нахождения коэффициентов (весов входов нейронов) и свободных членов в уравнениях разделяющих гиперплоскостей.

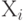 -
- 
