Элементы линейной алгебры
Элементы линейной алгебры
Упорядоченный ряд чисел называется вектором с числовыми координатами, последовательностью чисел, одномерным массивом, линейной таблицей . Таблица чисел часто называется также матрицей из чисел, последовательностью числовых векторов, двумерным массивом .
Горизонтальные ряды называются строками , вертикальные - столбцами , число aij - элементом, стоящим на пересечении i -ой строки и j -го столбца.
Пример. Ряд (вектор, одномерный массив) с именем a из элементов a1, a2,..., an, скажем, ряд 1, 4, -5, 0, 6,5. Таблица (матрица, двумерный массив) с именем B:
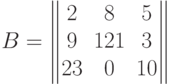
Размерность вектора определяется количеством элементов в ряде, размерность матрицы - числом строк и столбцов (обозначают размерность как  , где m - число строк, n - число столбцов матрицы).
, где m - число строк, n - число столбцов матрицы).
Матрицы часто обозначают кратко одной буквой, например, матрица A, или так:
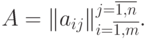
Если число строк в матрице m и число столбцов n матрицы будут равны, то она называется квадратной или матрицей порядка m(n) .
Нулевая матрица (нуль-матрица) - матрица вида
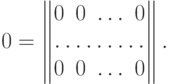
Единичная матрица (тождественная матрица)

Главная диагональ матрицы - это диагональ, ведущая из левого верхнего угла матрицы (от элемента с индексами [1, 1] ) в нижний правый угол, к элементу с индексами [n, n] . Побочная диагональ ведет из правого верхнего угла (от элемента [1, n] ) - в нижний левый угол (к элементу [n, 1] ).
Для того, чтобы найти (выделить) произвольный элемент a[i,j] матрицы, нужно указать оба его индекса i, j.
Матрица называется симметричной, если все элементы, расположены симметрично относительно главной диагонали, равны, то есть aij=aji .
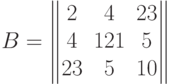
Пусть дана некоторая матрица A размерности m строк и n столбцов (коротко такая матрица обозначается 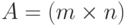 ):
):
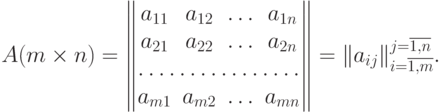
Если матрица B имеет только один столбец (n=1), то она называется матрицей-столбцом (вектор-столбцом):
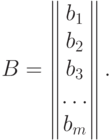
Если строки матрицы 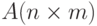 превратить в столбцы, а столбцы - в строки, то получим другую матрицу
превратить в столбцы, а столбцы - в строки, то получим другую матрицу 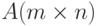 , которая называется транспонированной к матрице A :
, которая называется транспонированной к матрице A :
![A&(m\times n) =
\begin{Vmatrix}
a_{11} & a_{21} & \dotsc & a_{n1} \\
a_{12} & a_{22} & \dotsc & a_{n2} \\[-3pt]
\hdotsfor{4} \\
a_{1m} & a_{2m} & \dotsc & a_{nm}
\end{Vmatrix} .](/sites/default/files/tex_cache/89a830ffc5b0e51b913c0885ba014f31.png)
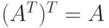 .
.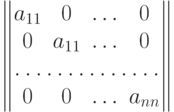
 называется верхней треугольной ( нижней треугольной ), если она имеет вид
называется верхней треугольной ( нижней треугольной ), если она имеет вид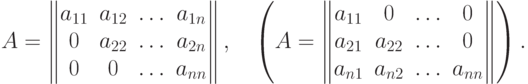
Определителем матрицы порядка n или детерминантом n -го порядка называется квадратная таблица из n строк (именуемых координатными) и n столбцов (именуемых векторными):
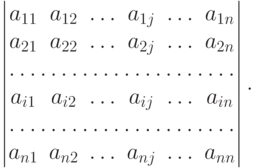
Обозначают определитель  , A= |aij|.
, A= |aij|.
С каждым определителем A связано одно число, называемое значением определителя и обозначаемое как |A| или 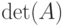 . Число A вычисляется следующим образом: берется по одному числу из каждой строки и из каждого столбца, составляются всевозможные произведения n элементов и затем из полученных n! произведений составляется алгебраическая сумма, при помощи определенным образом выбранных знаков " + " или " - " для произведений. Покажем это на примерах.
. Число A вычисляется следующим образом: берется по одному числу из каждой строки и из каждого столбца, составляются всевозможные произведения n элементов и затем из полученных n! произведений составляется алгебраическая сумма, при помощи определенным образом выбранных знаков " + " или " - " для произведений. Покажем это на примерах.
Пример. Определитель 1-го порядка A=|a11|=a11.

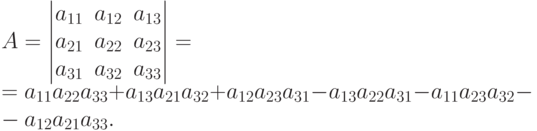
Алгебраическим дополнением Aij элемента aij определителя n -го порядка называется определитель (n-1) -го порядка, получаемый вычеркиванием i -ой строки и j -го столбца, на пересечении которых стоит элемент aij, причем Aij берется со знаком (-1)i+j .
Квадратная матрица A называется неособенной, невырожденной, если 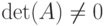 . Если же
. Если же 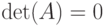 , то матрица A называется особой, вырожденной .
, то матрица A называется особой, вырожденной .
Присоединенной ( союзной ) матрицей к матрице 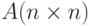 называется матрица
называется матрица  , элементами которой являются алгебраические дополнения элементов определителя транспонированной матрицы
, элементами которой являются алгебраические дополнения элементов определителя транспонированной матрицы  , то есть
, то есть
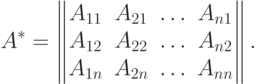
Пример. Если
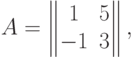
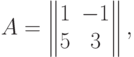
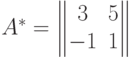 .
.Две матрицы одинаковой размерности 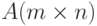 ,
, 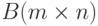 равны, если совпадают все элементы с одинаковыми индексами:
равны, если совпадают все элементы с одинаковыми индексами:
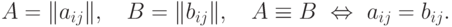
Суммой ( разностью ) матриц 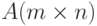 ,
, 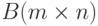 называется матрица
называется матрица 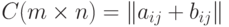 .
.
Произведением матрицы A и числа  называется матрица
называется матрица 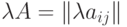 .
.
Пример. Пусть
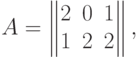
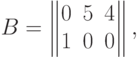
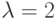 . Тогда находим сумму
. Тогда находим сумму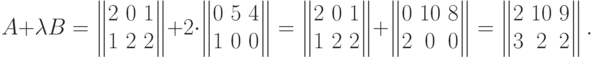
Матрица, полученная умножением числа 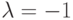 на матрицу A, называется противоположной к A и обозначается -A. Матрица, полученная сложением матрицы A с матрицей -B, называется разностью матриц A и B .
на матрицу A, называется противоположной к A и обозначается -A. Матрица, полученная сложением матрицы A с матрицей -B, называется разностью матриц A и B .
