Элементы линейной алгебры
Системой m линейных алгебраических уравнений с n неизвестными x1, x2,..., xn называют совокупность уравнений (каждое из которых может содержать от 1 до n неизвестных):
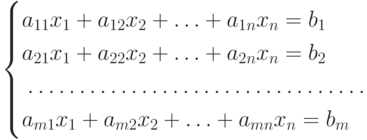
Решением системы называется совокупность чисел x1, x2,..., xn, которые обращают каждое уравнение системы в верное числовое равенство (тождество).
Система называется совместной, если существует хотя бы одно решение, а в противном случае, - несовместной . Если система имеет только одно решение, то она называется определенной, разрешимой единственным образом . Если имеется два и более решений, то система называется неопределенной .
Рассмотрим три матрицы вида
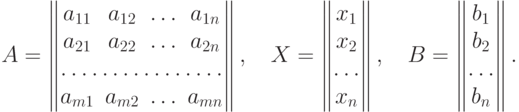
С помощью этих матриц систему уравнений можно записать в виде: AX=B. Это равенство проверяется непосредственно, используя правило перемножения матриц и условие равенства двух матриц. Такое равенство называется матричной записью системы уравнений.
Если 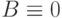 , то система называется однородной . Всякая однородная система совместна, так нулевой вектор X=0 всегда удовлетворяет соответствующему матричному уравнению.
, то система называется однородной . Всякая однородная система совместна, так нулевой вектор X=0 всегда удовлетворяет соответствующему матричному уравнению.
Если m=n (то есть A - квадратная матрица  ), то система называется системой из n уравнений с n неизвестными или системой порядка n. В этом случае можно говорить об определителе
), то система называется системой из n уравнений с n неизвестными или системой порядка n. В этом случае можно говорить об определителе 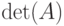 , который именуется определителем системы.
, который именуется определителем системы.
Рассмотрим эту систему отдельно:
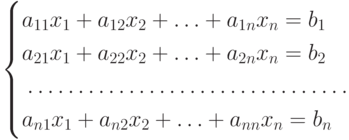
Из множества существующих методов решения систем уравнений мы рассмотрим два метода - метод Крамера и метод Гаусса.
Теорема(Крамера).
Если 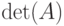 системы не равен нулю, то система имеет единственное решение, определяемое по формулам (Крамера):
системы не равен нулю, то система имеет единственное решение, определяемое по формулам (Крамера):
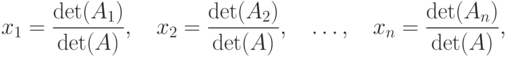
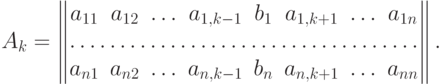
Метод Гаусса является одним из самых простых и самых старых. Этот метод реализуется так называемой вычислительной схемой (алгоритмом) единственного деления (или схемой с выбором ведущего элемента). Мы рассмотрим теперь систему общего вида.
Решим этим методом (шагами, этапами схемы) систему
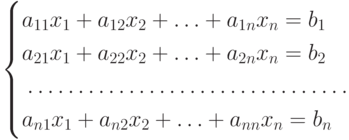
1-ый шаг. Пусть (для простоты рассуждений) 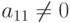 . Если это не так, то меняем местами уравнения, чтобы было выполнено это условие. Разделив первое уравнение на
. Если это не так, то меняем местами уравнения, чтобы было выполнено это условие. Разделив первое уравнение на 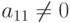 , получим:
, получим:
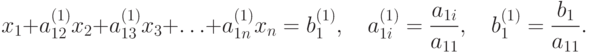
Умножая это уравнение поочередно на a21, a31, ..., an1 и вычитая полученные после этого уравнения поочередно из 2 -го, 3 -го, ..., n -го уравнений исходной системы, получим эквивалентную ей систему вида
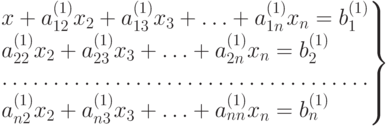
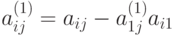 , при j,
, при j, 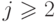 ;
; 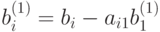 ,
,  . К последнему (n-1) -му уравнению системы снова применим указанные выше действия.
. К последнему (n-1) -му уравнению системы снова применим указанные выше действия.2-ой шаг. Пусть 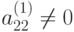 . Делим второе уравнение системы, полученной из исходной на предыдущем этапе, на
. Делим второе уравнение системы, полученной из исходной на предыдущем этапе, на 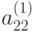 ; умножаем полученное уравнение соответственно на
; умножаем полученное уравнение соответственно на 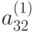 ,
, 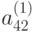 , ...,
, ..., 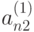 и вычитаем из 3-го, 4-го, ..., n -го уравнений; в результате второго этапа получим следующую систему:
и вычитаем из 3-го, 4-го, ..., n -го уравнений; в результате второго этапа получим следующую систему:
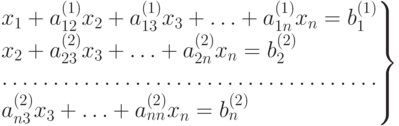
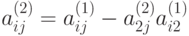 ,
, 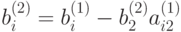 ,
, 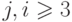 .
.n-й шаг. В результате выполнения n шагов получим систему вида
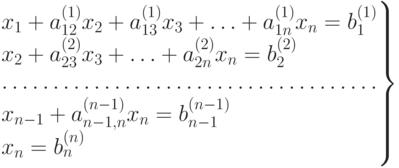
Проделанная совокупность n шагов называется прямым ходом метода Гаусса . Решение системы находится с помощью обратного хода метода Гаусса, который состоит в следующем.
Из последнего уравнения находим xn, затем подставляем это значение в предпоследнее уравнение и находим xn-1, затем оба x_n и xn-1 подставляем в (n-2) -е уравнение и находим xn-2 и т.д., пока не найдем из 1 -го уравнения последнее неизвестное x_1.
Под пространством мы до сих пор понимали реально существующее пространство трех измерений: ширины, длины и высоты. Результатом такого процесса абстрагирования от конкретной сущности 1, 2, 3-мерных пространств явилось понятие n -мерного пространства (пространства размерности n, n>3 ). Это есть результат обобщения геометрического пространства. Могут быть рассмотрены различные типы абстрактных многомерных (размерности 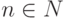 ) и даже бесконечномерных пространств.
) и даже бесконечномерных пространств.
Множество E назовем линейным пространством, а его элементы - векторами этого пространства, если:
- для любых двух элементов
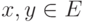 определяется элемент, называемый их суммой и обозначаемый x+y ;
определяется элемент, называемый их суммой и обозначаемый x+y ; - для каждого элемента
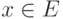 и любого числа
и любого числа 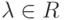 можно определить элемент из E, называемый произведением
можно определить элемент из E, называемый произведением  на x и обозначаемый как
на x и обозначаемый как 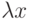 ;
; - для любых элементов
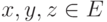 и любых чисел
и любых чисел 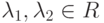 выполнены следующие аксиомы:
выполнены следующие аксиомы:- x+y=y+x ;
- (x+y)+z=x+(y+z) ;
-
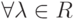 ,
, 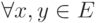 :
:  ;
; -
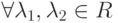 ,
, 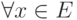 :
: 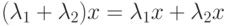 ;
; -
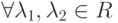 ,
, 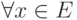 :
: 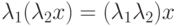 ;
; - существует нулевой элемент (обозначаемый как 0 ) пространства:
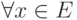 , x+0=x ;
, x+0=x ; -
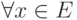 существует противоположный ему элемент (обозначаемый как -x ) такой, что x+(-x)=0 ;
существует противоположный ему элемент (обозначаемый как -x ) такой, что x+(-x)=0 ; - существует единичный элемент (обозначаемый как 1 ):
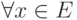 ,
, 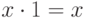 .
.
Множество всех упорядоченных наборов из n чисел 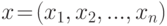 для которых определены операции сложения и умножения этих наборов и умножения набора на число по законам, приведенным выше, называется n -мерным арифметическим пространством . Число n - размерность пространства, элемент x=(x1, x2,..., xn) - вектор пространства, а числа xi - координаты вектора x .
для которых определены операции сложения и умножения этих наборов и умножения набора на число по законам, приведенным выше, называется n -мерным арифметическим пространством . Число n - размерность пространства, элемент x=(x1, x2,..., xn) - вектор пространства, а числа xi - координаты вектора x .
Обозначают n -мерное векторное пространство через Rn.
Линейное пространство называют евклидовым, если в нем определено скалярное произведение, удовлетворяющее свойствам скалярного произведения векторов (см. выше).
Обозначают евклидово пространство размерности n через En.
Пространство X называется метрическим (метризуемым), если в этом пространстве можно определить некоторым образом метрику 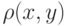 любых двух элементов или аналог расстояния между элементами x, y , причем вводимое расстояние должно удовлетворять аксиомам метрики (расстояния):
любых двух элементов или аналог расстояния между элементами x, y , причем вводимое расстояние должно удовлетворять аксиомам метрики (расстояния):
Нормой вектора x=(x1, x2,..., xn) в евклидовом пространстве называется неотрицательный скаляр (число)

"Норма" вектора является обобщением понятия "длина" геометрического вектора и удовлетворяет следующим законам:
-
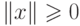 ,
, 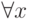 , |x|=0
, |x|=0  x=0 ( аксиома неотрицательности и равенства нулю );
x=0 ( аксиома неотрицательности и равенства нулю ); -
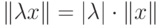 ( аксиома однородности );
( аксиома однородности ); -
 ( аксиома треугольника )
( аксиома треугольника ) -
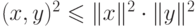 ( неравенство Коши-Буняковского ).
( неравенство Коши-Буняковского ).
Пусть n -мерные векторы a1, a2, ..., ak. Вектор
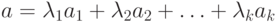
Естественным базисом n-мерного пространства или базисными векторами называются векторы вида 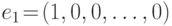 ,
, 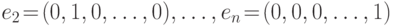 . Любой вектор n -мерного пространства является линейной комбинацией базисных векторов. Коэффициентами n -мерного вектора при представлении его в виде линейной комбинации базисных векторов служат координаты вектора.
. Любой вектор n -мерного пространства является линейной комбинацией базисных векторов. Коэффициентами n -мерного вектора при представлении его в виде линейной комбинации базисных векторов служат координаты вектора.
Пример. Действительно, легко проверить, что любой вектор x=(x1,x2,...,xn) представим как x=x1 e1+x2e2+...+xn en.
Арифметический вектор x=(x1, x2, ..., xn) из En можно понимать как направленный отрезок в n -мерном геометрическом пространстве, а базис (e1,e2,...,en) - как попарно перпендикулярные орты n -мерной системы координат. Векторы x1, x2,...,xk из n -мерного пространства называются линейно-независимыми, если равенство  справедливо только при нулевых значениях всех постоянных. Если равенство возможно при каком-то хотя бы одном
справедливо только при нулевых значениях всех постоянных. Если равенство возможно при каком-то хотя бы одном 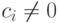 , то x1, x2, ..., xk называют линейно-зависимыми .
, то x1, x2, ..., xk называют линейно-зависимыми .
Пример.
Векторы e_1=(1,0,0), e_2=(0,1,0), e3=(0,0,1) линейно-независимы, так как справедлива эквивалентность: c1e1+c2e2+c3e3= (c1,c2,c3)=0  c1=c2=c3. Векторы a_1=(1,2,3), a_2=(2,4,6) - линейно-зависимые, так как c1a1+c2a2=0 при c1=2, c2=-1.
c1=c2=c3. Векторы a_1=(1,2,3), a_2=(2,4,6) - линейно-зависимые, так как c1a1+c2a2=0 при c1=2, c2=-1.
Если векторы x1, x2,..., xk линейно-зависимы, то по крайней мере один из них является линейной комбинацией остальных. Например, если  , то
, то
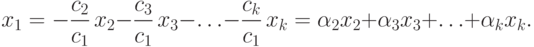

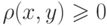 ,
, 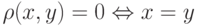 (
( (асксиома симметрии);
(асксиома симметрии);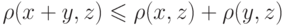 (
(