Уравнения и неравенства

Уравнения и неравенства

Один из основных вопросов, который "занимает" математиков - решение различных рода и типа уравнений или неравенств, систем уравнений (неравенств) или, как говорят математики, исследование уравнений на их разрешимость. Это выражение включает множество смежных аспектов - вывод уравнения (неравенства), нахождение решения, выяснение его однозначности, единственности и т.д. Нас будут интересовать два основных вопроса (как "нематематика") - вывод уравнения (неравенства) и нахождение его решения (хотя другие вопросы иногда могут оказаться не менее значимыми, интересными и сложными).

Уравнением называется некоторое определенное равенство, связывающее хотя бы один неизвестный объект (из некоторого, заранее определенного множества объектов) хотя бы с одним известным объектом из этого (чаще всего) или из другого множества.Если эти объекты - числового происхождения, то уравнение называется числовым (скалярным). Если объекты - векторы, то уравнение называется векторным. Если объекты - матрицы, то уравнение называется матричным и т.д.

Решением уравнения называется любое конкретное значение неизвестного объекта, которое при подстановке в уравнение превращает его в верное (истинное) равенство, то есть в тождество. Если такой допустимый объект не существует, то уравнение не имеет решения или неразрешимо в данном множестве объектов. Множество допустимых значений неизвестного объекта называется допустимым множеством решений или областью определения уравнения .

Количество известных и неизвестных объектов уравнения существенно влияет на разрешимость уравнения.

Пример. Уравнение 2x+3=7 - простое скалярное уравнение, относительно неизвестного числа x. Уравнение 2x+3y=z - также скалярное, но уже относительно трех неизвестных. Это уравнение - несравнимо более сложное и в общем виде не имеющее решения (то есть не имеющее метода, алгоритма поиска неизвестных x, y, z ).

Если решается уравнение вида f(x)=0 и найдено его решение x=a (иначе говоря, f(a)=0 ), то x=a называют нулем функции f(x) .

Неравенство - некоторое соотношение, связывающее неизвестный объект (неизвестные объекты) с известными объектами с помощью знаков неравенства (знаков , , , <, > ).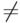

Неравенства, как и уравнения, могут быть различного типа: скалярные, векторные и т.д.

Решение системы уравнений (неравенств) должно обращать в тождество каждое уравнение (неравенство) системы. Для решения системы уравнений (неравенств) необходимо решить каждое уравнение (неравенство), найти множества решений каждого уравнения (неравенства) и взять их пересечение (то есть подмножество, где каждое уравнение или неравенство обращается в верное числовое равенство или неравенство).

Решить уравнение ( неравенство ) означает найти все допустимые объекты, превращающие уравнение (неравенство) в истинное равенство (неравенство). Решением уравнения (неравенства) называют часто также и сам процесс нахождения таких объектов.

Пример. Получим (как говорят математики, "выведем") и затем решим скалярное уравнение (уравнение с числовым неизвестным) по следующим исходным данным (по следующей содержательной постановке задачи): расстояние между станциями A и B по железной дороге равно 96 км, при этом первый поезд, идущий со средней скоростью на 12 км/час больше, чем второй, проходит это расстояние на 40 мин. быстрее, чем второй; необходимо найти скорости обоих поездов. Для получения уравнения проанализируем условие задачи и выпишем содержательно связь между параметрами (элементами) задачи, то есть выпишем содержательное уравнение вида (Время на AB второго поезда) - (Время на AB первого поезда) = 40 мин.

Теперь видно, что для нахождения неизвестных объектов (времени) этого уравнения необходимо ввести неизвестное - скорость (так как путь известен). Итак, обозначим через x (км/час) - скорость первого поезда, тогда скорость второго поезда будет по условию задачи равна x-12 (км/час). Из содержательно и не формализованно записанного соотношения, получаем уже формализованное, алгебраическое уравнение вида

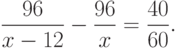
Решаем это уравнение. Для этого приводим к общему знаменателю: .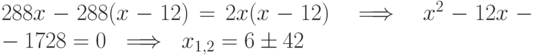

Отбрасывая затем один из неподходящих двух корней ( x=-36 ), получаем скорость первого поезда - 48 км/час, а скорость второго поезда (находим по условию задачи) - 36 км/час.

Особый класс уравнений и неравенств образуют уравнения и неравенства, связывающие текущие координаты точки на прямой, плоскости, пространстве и описывающие геометрические свойства, геометрическую (топологическую) структуру множества точек, удовлетворяющих такому соотношению, то есть решений таких уравнений или неравенств. Такие уравнения часто называют уравнениями линий, поверхностей (фигур, тел).

Рассмотрим некоторые основные, простые (канонические, как говорят в математике) типы таких уравнений и неравенств. Отметим попутно, что уравнения, определяющие линии на плоскости, часто в каноническом виде представлять не удается.

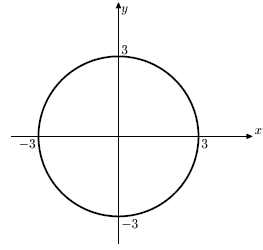
Окружность - это геометрическое место точек плоскости, отстоящих от некоторой фиксированной точки M(x₀; y₀) (называемой центром окружности) на одинаковом расстоянии r (называемой радиусом окружности). Задается неявным уравнением (x-x₀)²+(y-y₀)²=r².

Пример. Уравнение окружности с центром в начале координат и радиусом, равным 3 единицы масштаба координатной системы, можно изобразить как на рис. 6.1.

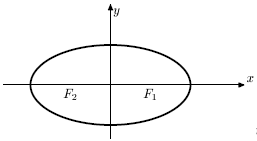
Эллипс - это геометрическое место (рис. 6.2) точек M(x;y), сумма расстояний от каждой из которых до двух данных точек F₁ и F₂, называемых фокусами, есть величина постоянная.

Выведем уравнение эллипса. Пусть, согласно определению эллипса, r₁+r₂= |F₂M| + |F₁M| =2a.

Рис. 6.1. График окружности

Легко проверить (по известной из школы формуле расстояния между двумя точками), что верны следующие равенства:

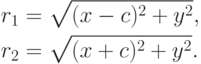
Поэтому из равенства r₁+r₂=2a получаем:

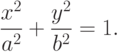
Это уравнение называется каноническим уравнением эллипса, величины r₁ и r₂ - фокальные радиусы точки M(x;y), F₁, F₂ - фокусы эллипса, x=0, y=0 - оси симметрии, величина 2a - большая ось, 2b - малая ось, 2c=|F₁F₂| - фокусное расстояние, величина 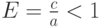- эксцентриситет эллипса.

Рис. 6.2. График эллипса