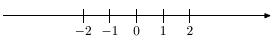Координаты и векторы
Координаты и векторы
Числовой осью называется бесконечная прямая, на которой определены: точка O - начало отсчета; положительное направление, указываемое стрелкой; масштаб измерения (принцип отложения чисел на оси, часто с указанием единицы измерения). Условное изображение числовой прямой (числового луча) приведено на рис. 3.1.
Для каждого действительного числа x на числовой оси R определена единственная точка, соответствующая его количеству (изображающая это число с учетом выбранного масштаба и отсчета) и наоборот, то есть совокупность R и множество точек числовой оси могут быть связаны общим, однозначно определяемым правилом, законом.
Пример. Числу 5 на числовой оси соответствует точка, удаленная на расстояние в 5 единиц масштаба от начальной точки (точки отсчета 0 ).
Пример. Точке A, удаленной на расстояние 3 единицы масштаба от начала координат O можно сопоставить число 3.
Числовая прямая, расположенная обычно на плоскости горизонтально к рассматривающему, называется осью x ( Ox ), а числовая прямая, расположенная обычно вертикально к нему, - осью y (Oy) .Эти прямые образуют систему ориентации каждой точки на плоскости по двум ее координатам.
Плоскость, определяемая этими двумя перпендикулярными (или, как говорят в математике, ортогональными) числовыми прямыми, называется плоскостью xy (xOy) .
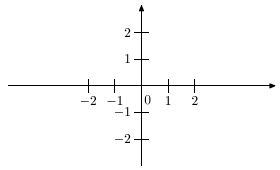
Каждая пара вещественных значений (x;y) задает одну единственную точку M(x;y) на этой плоскости, которая определяется как точка пересечения перпендикулярных (ортогональных) прямых, проходящих через значения x оси Ox и значение y оси Oy. Наоборот, каждой точке (x;y) можно сопоставить пару вещественных чисел: x - на оси Ox и y - на оси Oy. Так определенная система двух перпендикулярных числовых прямых называется прямоугольной декартовой системой координат на плоскости (рис. 3.2).
Оси координат обычно помечаются буквами.
Ось Ox называется осью абсцисс , ось Oy - осью ординат .Эти оси делят плоскость xOy на 4 части (координатных угла или, как их еще называют, квадранта).
Упорядоченная система трех взаимно перпендикулярных осей с общим началом отсчета (началом координат) и общей единицей измерения длины (масштабом) называется прямоугольной декартовой системой координат в пространстве .Обозначается такая система Oxyz или xyz. Ось Ox называется осью абсцисс, Oy - осью ординат, Oz - осью аппликат .
Кроме декартовой системы координат, часто используют и другие удобные, не обязательно прямоугольные, системы координат.
Одной из наиболее часто используемых является полярная система координат, определяющая, как и в декартовой системе, однозначное положение точки на плоскости с помощью двух параметров.
Возьмем на плоскости точку O (называемую полюсом ) и выходящую из этой точки полупрямую (называемую полярной осью ). Если на этой прямой задать масштаб и положительное направление, то мы определим полярную систему координат. Положение точки M на плоскости в полярной системе координат задается двумя числовыми величинами:  - расстоянием точки M от полюса, то есть
- расстоянием точки M от полюса, то есть 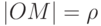 и
и  - углом, образованным отрезком OM с положительным направлением полярной оси. Обозначим точку с полярными координатами в виде
- углом, образованным отрезком OM с положительным направлением полярной оси. Обозначим точку с полярными координатами в виде 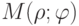 . Обычно считают, что
. Обычно считают, что 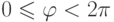 ,
, 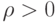 . Эти значения называются главными значениями. Каждая точка на плоскости однозначно определяется полярными
координатами. Исключение составляет единственная точка
. Эти значения называются главными значениями. Каждая точка на плоскости однозначно определяется полярными
координатами. Исключение составляет единственная точка  , где угол
, где угол  может быть любым. Условно, в этом случае берется угол
может быть любым. Условно, в этом случае берется угол 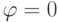 .
.
Найдем зависимость между координатами точки M(x;y) в прямоугольной декартовой системе координат и ее координатами 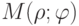 в полярной системе.
в полярной системе.
Построим прямоугольную систему xOy, где ось Ox совпадает с полярной осью, O(0;0) - начала координат, а положительные направления этих осей совпадают (рис. 3.3).
Используя прямоугольные треугольники и тригонометрические функции, получим следующие основные соотношения:
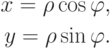
Таким образом, зная полярные координаты точки, можно найти прямоугольные координаты этой же точки. Кроме того, если использовать основное тригонометрическое соотношение и определение тангенса угла из школьного курса (нужно сложить квадраты x, y, а затем поделить y на x ), то справедливы следующие соотношения:

Пример.
Если  ,
, 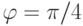 , то
по соответствующим формулам получаем
, то
по соответствующим формулам получаем
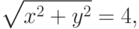
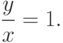
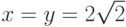 .
.Пример. Уравнение окружности с центром в начале координат и радиуса r в декартовой системе координат, как известно, имеет вид: x2+y2=r2. Уравнение окружности в полярных координатах будет иметь вид

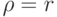 .
Кроме того, это уравнение освобождено от "лишнего"
параметра
.
Кроме того, это уравнение освобождено от "лишнего"
параметра  , который в данном случае считается любым
из диапазона
, который в данном случае считается любым
из диапазона 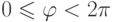 . Работать с объектами
в полярной системе координат часто проще на практике, в геодезии,
астрономии и др.
. Работать с объектами
в полярной системе координат часто проще на практике, в геодезии,
астрономии и др.Удобной в пространстве системой координат является и так называемая сферическая система координат. В этой системе положение точки M(x;y;z) в пространстве однозначно определяется ее расстоянием r от начала координат (длиной отрезка OM ), углом 
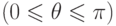 между OM и положительной полуосью Oz и углом
между OM и положительной полуосью Oz и углом  (
( 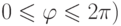 между проекцией OM на плоскость xOy и положительной полуосью Ox (рис. 3.4).
между проекцией OM на плоскость xOy и положительной полуосью Ox (рис. 3.4).
Выясним форму связи сферических и декартовых координат. По рис. 3.4:
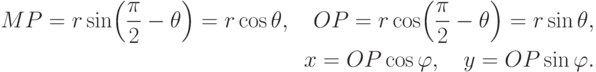
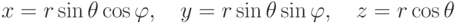 .
.