|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Измерение нагрузки
Принципы и методы измерения
Технические возможности для измерения являются решающими для того, что измерено и как проводятся измерения. Первая управляемая программа измерения оборудования была разработана в Техническом Университете Дании и описана в (Andersen & Hansen & Iversen, 1971 [2]). Любое измерение нагрузки в процессе её обслуживания, дискретное по состояниям или непрерывное по времени, может в принципе быть реализовано, используя одновременно два основных фактора.
-
Число событий.
Это может быть, например, числом ошибок, число попыток вызова, число ошибок в программе, число работ в очереди к вычислительному центру и т.д.
-
Временные интервалы.
Например, времена сеанса связи, времена выполнения задач в компьютере, времена ожидания и т.д.
Комбинируя эти два фактора, мы можем получить любую характеристику процесса нагрузки. Самая важная характеристика - объем обслуженного трафика, то есть сумма всего времени пребывания в системе (интервал) в пределах данного периода измерения.
С функциональной точки зрения все методы, измеряющие нагрузку, могут быть разделены на следующие два класса.
- Непрерывные методы измерения.
- Дискретные методы измерения.
Непрерывные методы измерения
В этом случае измеряющая точка активна, и она активизирует измеряющее оборудование в момент события. Даже если метод измерения непрерывный, результат может быть дискретным.
Пример 15.1.1: Измерение оборудования: непрерывное время
Приведем примеры оборудования, работающего согласно непрерывному принципу.
(а). Электромеханические счетчики, которые увеличиваются на единицу в момент события.
(б) Записывающие х-у координатографы, подключенные к точке, которая является активной в течение всего времени подключения.
(в) Счетчики ампер-часов, которые интегрируют потребление мощности в течение периода измерения. Когда-то они применялись для измерения нагрузки в старых электромеханических станциях. Каждый пучок каналов был подключен через резистор 9,6 К, в течение всего времени занятия между заземлением и 48 вт и таким образом каждое соединение потребляло 5 мА.
(г) Водомеры, которые измеряют потребление воды в домашнем хозяйстве.
Дискретные измерения
В этом случае измеряющая точка пассивна, а измеряющее оборудование должно самостоятельно проверять (опрашивать), были ли изменения в точках измерения (обычно это двоичные значения включено/ выключено).
Этот метод называется методом сканирования, и опрос обычно делается в регулярные моменты времени (постоянные детерминированные временные интервалы). Все события, которые произошли между двумя последовательными моментами сканирования, обнаруживаются только в последний момент и рассматриваются как произошедшие именно в этот момент.
Пример 15.1.2: Измерение оборудования: дискретное время
Примеры оборудования, работающего дискретно.
(а) Оплата вызова, согласно принципу Карлссона, где импульсы оплаты вырабатываются в регулярные моменты времени, а период опроса зависит от стоимости в единицу времени. Он измеряет время занятия абонента, который инициировал вызов. Каждый временной модуль (шаг) соответствует некоторой сумме денег. Если мы измеряем продолжительность вызова его стоимостью, то наблюдаем дискретное распределение (0, 1, 2., единиц времени). Метод называют по имени S.A. Karlsson из Финляндии (Karlsson, 1937 [57]). По сравнению с большинством других методов ему требуются минимум администрирования.
(б) Обслуженная нагрузка пучком каналов электромеханической станции практически измеряется согласно принципу опроса. В течение одного часа мы смотрим число занятых пучков каналов 100 раз (каждые 36 секунд) и складываем эти числа на механическом счетчике, который, таким образом, указывает среднюю обслуженную нагрузку с точностью в два десятичных числа. Также, отсчитывая число вызовов, мы можем оценить среднее время пребывания в системе.
(в) Принцип опроса особенно подходит для реализации в цифровых системах. Например, управляемое процессором оборудование, разработанное в DTU (Технический Университет Дании) в 1969 г., было способно проверить 1024 точки измерения (электронномеханические станции, пучки каналов или каналы) в пределах 5 миллисекунд. Состояние каждой точки измерения (свободно/занято или включено/выключено) сохраняется в памяти и в памяти же фиксируются результаты двух последних опросов. Сравнивая их, мы получаем возможность обнаружить изменения состояния точки сканирования. Изменение состояния из 0 в 1 соответствует началу занятия и из 1 в 0 - завершению занятия. Сканирование управляется тактовым генератором, поэтому мы можем контролировать каждый канал в течение заданного времени и задавать временные интервалы измерения. Таким образом, можно определять распределения времени.
Классическое оборудование (эрлангометры) наблюдают за нагрузкой по числу приборов, находящихся в заданном состоянии ( вертикальный способ наблюдений, имеющий числовое представление), а программы управления оборудованием наблюдают за нагрузкой по времени в дискретные моменты времени ( горизонтальный способ наблюдения, представленный с помощью числа интервалов сканирования). Количество информации почти не зависит от интервала сканирования, а только от числа изменений состояний (время сканирования измеряется целым числом интервалов сканирования). Методы измерения имеют решающее влияние на мышление и способы формулирования и анализа статистических проблем. Классическое оборудование, наблюдающее за состояниями, подразумевало, что статистические исследования проводятся на основе вероятностей состояний, то есть на основе процесса "гибели и размножения". С математической точки зрения эти модели были довольно сложны. Приводимые ниже выводы находятся по сравнению с ними на элементарном уровне. Они получены в процессе работы над программой управления оборудованием в пространстве времени (Iversen, 1976 [36]) ( горизонтальные измерения ).
Теория дискретизации
Предположим, что мы имеем выборку я независимых и равномерно распределенных ( IID - Independent and Identically Distributed ) величин наблюдения 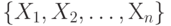 случайной переменной с неизвестной конечной средней величиной
случайной переменной с неизвестной конечной средней величиной 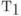 , и конечной дисперсией
, и конечной дисперсией  (статистические параметры).
(статистические параметры).
Средняя величина и дисперсия выборки определены следующим образом:
 |
( 15.1) |
 |
( 15.2) |
 и
и 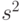 - функции случайной переменной и поэтому также случайные переменные, определенные распределением, которое мы называем распределением выборки.
- функции случайной переменной и поэтому также случайные переменные, определенные распределением, которое мы называем распределением выборки.  является центральной оценкой неизвестной средней величины совокупности
является центральной оценкой неизвестной средней величины совокупности  то есть:
то есть:
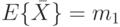 |
( 15.3) |
Кроме того, 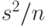 - центральная оценка неизвестной дисперсии выборки - означает
- центральная оценка неизвестной дисперсии выборки - означает  , то есть:
, то есть:
 |
( 15.4) |
Мы отображаем точность оценки типового параметра посредством доверительного интервала, который с данной вероятностью определяет, как оценка соотносится с неизвестным теоретическим значением. В нашем случае доверительный интервал средней величины равен:
 |
( 15.5) |
где 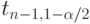 , а верхний квантиль
, а верхний квантиль  t-распределения Стьюдента с я-1 степени свободы. Вероятность, с который доверительный интервал включает неизвестную теоретическую среднюю величину, равен (1 - а) и называется доверительным уровнем. Некоторые значения t-распределения Стьюдента даются в Таблице 15.1. Когда п становится большим, тогда t-распределение Стьюдента сходится к нормальному распределению, и мы можем использовать квантиль этого распределения. Предположение о независимости выполняется для измерений, взятых в различные дни, но, например, не для последовательных измерений методом сканирования в пределах ограниченного временного интервала, потому что число занятых каналов в данный момент будет коррелировать с числом занятых каналов в предыдущем и следующем сканировании.
t-распределения Стьюдента с я-1 степени свободы. Вероятность, с который доверительный интервал включает неизвестную теоретическую среднюю величину, равен (1 - а) и называется доверительным уровнем. Некоторые значения t-распределения Стьюдента даются в Таблице 15.1. Когда п становится большим, тогда t-распределение Стьюдента сходится к нормальному распределению, и мы можем использовать квантиль этого распределения. Предположение о независимости выполняется для измерений, взятых в различные дни, но, например, не для последовательных измерений методом сканирования в пределах ограниченного временного интервала, потому что число занятых каналов в данный момент будет коррелировать с числом занятых каналов в предыдущем и следующем сканировании.
В следующей секции мы вычисляем среднюю величину и дисперсию при измерении нагрузки в течение, например, одного часа. Это суммарное значение в течение данного дня может использоваться как единственное наблюдение в приведенной выше формуле, где мы имеем измерение с числом наблюдений равным числу дней.
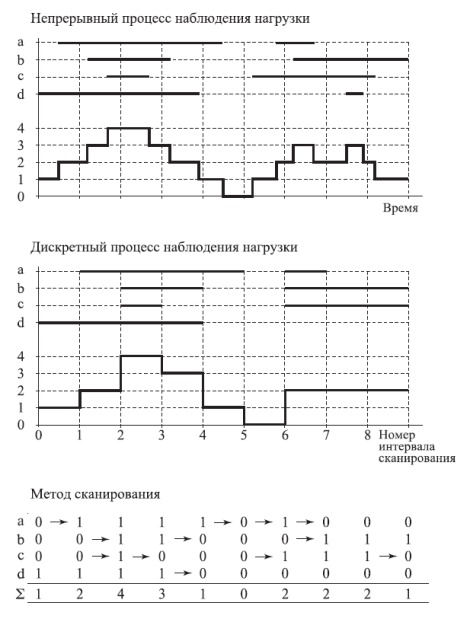
Рис. 15.1. Наблюдение процесса нагрузи! непрерывным методом измерения и методом сканирования с регулярными интервалами сканирования. При методе сканирования достаточно наблюдать только изменения состояния
 |
 =10% =10% |
 =5% =5% |
 =1% =1% |
|---|---|---|---|
| 1 | 6.314 | 12.706 | 63.657 |
| 2 | 2.920 | 4.303 | 9.925 |
| 5 | 2.015 | 2.571 | 4.032 |
| 10 | 1.812 | 2.228 | 3.169 |
| 20 | 1.725 | 2.086 | 2.845 |
| 40 | 1.684 | 2.021 | 2.704 |
 |
1.645 | 1.960 | 2.576 |
Пример 15.2.1: Доверительный интервал для потерь по вызовам
На группе из 30 пучков каналов мы зафиксировали результат 500 попыток вызова. Это измерение повторено 11 раз, и мы находим следующие значения потерь по вызовам (в процентах):
{9,2; 3,6; 3,6; 2,0; 7,4; 2,2; 5,2; 5,4; 3,4; 2,0; 1,4}Полная сумма наблюдений равна 45,4, и сумма квадратов наблюдений - 247,88. Мы находим по формуле (1 5.1)  = 4,1273 % и согласно формуле (15.2)
= 4,1273 % и согласно формуле (15.2) 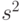 = 6,0502 (%). При 95 % уровне, используя значения /-уровней из Таблицы 15.1, получаем доверительный интервал (2.47 - 5.78). Заметим, что наблюдения получены при PCT-I нагрузке 25 Эрланг, которая предлагается 30 каналам. Согласно В-формуле Эрланга теоретическая вероятность блокировки - 5,2603 %. Это значение - в пределах доверительного интервала. Если мы хотим уменьшить доверительный интервал с коэффициентом 10, то должны сделать в 100 раз больше наблюдений (см. формулу 15.5), то есть 50 000 опросов на каждое измерение. Выполняя такое моделирование, заметим, что потери по вызовам равняются 5,245 % при доверительном интервале (5.093 - 5.398).
= 6,0502 (%). При 95 % уровне, используя значения /-уровней из Таблицы 15.1, получаем доверительный интервал (2.47 - 5.78). Заметим, что наблюдения получены при PCT-I нагрузке 25 Эрланг, которая предлагается 30 каналам. Согласно В-формуле Эрланга теоретическая вероятность блокировки - 5,2603 %. Это значение - в пределах доверительного интервала. Если мы хотим уменьшить доверительный интервал с коэффициентом 10, то должны сделать в 100 раз больше наблюдений (см. формулу 15.5), то есть 50 000 опросов на каждое измерение. Выполняя такое моделирование, заметим, что потери по вызовам равняются 5,245 % при доверительном интервале (5.093 - 5.398).
Непрерывные измерения с неограниченным периодом
Измерение временных интервалов непрерывными методами без ограничения периода измерения выполняется в соответствии с теорией дискретизации.
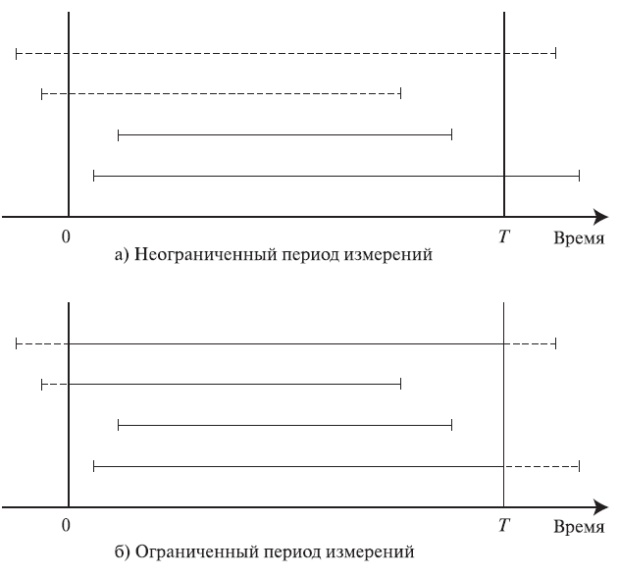
Рис. 15.2. При анализе измерений нагрузки мы различаем два случая: (а) Измерения при неограниченном периоде времени. При этом для всех вызовов, которые начались в течение периода измерения, учитывается их полная продолжительность, (б) Измерения в ограниченный период времени. Все вызовы вносят вклад как часть их времен пребывания в системе, которые расположены в течение периода измерения. При этом на рисунке часть времен пребывания в системе в течение периода измерения показаны сплошными линиями.
Для объема нагрузки или интенсивности нагрузки мы можем применить формулы (3.46) и (3.48) определения стохастической суммы. Они являются общими, единственное ограничение - это необходимость стохастической независимости между X и N. Практически это означает, что системы должны быть без потерь. Вообще мы будем иметь потери несколько процентов, а как худший случай принимать независимость этих величин. Более важный случай - Пуассоновский поток вызовов с интенсивностью  . Тогда мы получаем стохастическую сумму (секция 3.3). Для Пуассоновского потока вызовов, когда рассматривается временной интервал Т, мы имеем:
. Тогда мы получаем стохастическую сумму (секция 3.3). Для Пуассоновского потока вызовов, когда рассматривается временной интервал Т, мы имеем:
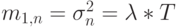
и отсюда находим:
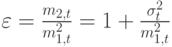 |
( 15.7) |
где 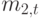 - второй (нецентральный) момент распределения времени пребывания в системе и
- второй (нецентральный) момент распределения времени пребывания в системе и  - коэффициент формы Пальма того же самого распределения:
- коэффициент формы Пальма того же самого распределения:
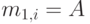 |
( 15.8) |
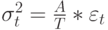 |
( 15.9) |
Распределение 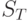 в этом случае будет составным Пуассоновским распределением (Feller, 1950 [27]). Формула соответствует объему нагрузки (например, в эрлангочасах). Для большинства приложений и параметров измерения нас интересует среднее число занятых каналов, то есть интенсивность нагрузки в единицу времени нагрузки
в этом случае будет составным Пуассоновским распределением (Feller, 1950 [27]). Формула соответствует объему нагрузки (например, в эрлангочасах). Для большинства приложений и параметров измерения нас интересует среднее число занятых каналов, то есть интенсивность нагрузки в единицу времени нагрузки 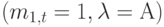 , когда мы выбираем среднее время пребывания в системе как единицу времени.
, когда мы выбираем среднее время пребывания в системе как единицу времени.
Эти формулы справедливы для произвольных распределений времени пребывания в системе. Формулы (15.8) и (15.9) первоначально были получены С. Пальмом (1941 [78]). Для специальных случаев 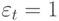 (постоянное время занятия) и
(постоянное время занятия) и 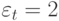 (экспоненциально распределенные времена пребывания в системе) эта формула была опубликована (Rabe, 1949 [85]). Вышеупомянутая формула справедлива для всех вызовов, прибывающих в интервале Т при измерении полной продолжительности во все время пребывания в системе независимо от того, какой величины это время пребывания (рис.15.2. а).
(экспоненциально распределенные времена пребывания в системе) эта формула была опубликована (Rabe, 1949 [85]). Вышеупомянутая формула справедлива для всех вызовов, прибывающих в интервале Т при измерении полной продолжительности во все время пребывания в системе независимо от того, какой величины это время пребывания (рис.15.2. а).

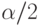 в обоих "хвостовых"** направлениях /-распределения Стьюдента. Когда
в обоих "хвостовых"** направлениях /-распределения Стьюдента. Когда