Основы теории защиты информации
Криптография (тайнопись) - это раздел математики, в котором изучаются и разрабатываются системы изменения письма с целью сделать его непонятным для непосвященных лиц. Известно, что еще в V веке до нашей эры тайнопись использовалась в Греции. В современном мире, где все больше и больше услуг предоставляется через использование информационных технологий, проблема защиты информации методами криптографии имеет первостепенное значение. Сегодня большая часть обмена информацией проходит по компьютерным сетям и часто (в бизнесе, военным и прочее) нужно обеспечивать конфиденциальность такого обмена. Теоретические основы классической криптографии впервые были изложены Клодом Шенноном в конце 1940-х годов.
Простейшая система шифрования - это замена каждого знака письма на другой знак по выбранному правилу. Юлий Цезарь, например, заменял в своих секретных письмах первую букву алфавита на четвертую, вторую - на пятую, последнюю - на третью и т.п., т.е. A на D, B на E, Z на C и т.п. Октавиан Август заменял каждую непоследнюю букву алфавита на следующую, а последнюю на первую. Подобные шифры, называемые простой заменой или подстановкой, описаны в рассказах "Пляшущие человечки" А. К. Дойла, "Золотой жук" Э. По и других.
Шифры простой замены легко поддаются расшифровке, при знании исходного языка сообщения, т.к. каждый письменный язык характеризуется частотой встречаемости своих знаков. Например, в английском языке чаще всего встречается буква E, а в русском - О. Таким образом, в шифрованном подстановкой сообщении на русском языке самому частому знаку будет с большой вероятностью соответствовать буква О. Вероятность будет расти с ростом длины сообщения.
Усовершенствованные шифры-подстановки используют возможность заменять символ исходного сообщения на любой символ из заданного для него множества символов, что позволяет выровнять частоты встречаемости различных знаков шифра, но подобные шифры удлиняют сообщение и замедляют скорость обмена информацией.
В шифрах- перестановках знаки сообщения специальным образом переставляются между собой, например, записывая сообщение в строки заданной длины и беря затем последовательность слов в столбцах в качестве шифра. Сообщение "ТЕОРИЯИНФОРМАЦИИ", используя строки длины 4, будет в шифрованном таким методом виде выглядеть как "ТИФАЕЯОЦОИРИРНМИ", потому что при шифровании использовался следующий прямоугольник:
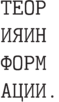
Шифры-перестановки в общем случае практически не поддаются дешифровке. Для их дешифровки необходимо знать дополнительную информацию. Крупный недостаток подобных шифров в том, что если удастся каким-то образом расшифровать хотя бы одно сообщение, то в дальнейшем можно расшифровать и любое другое. Модификацией шифров-перестановок являются шифры-перестановки со словом-ключом, которое определяет порядок взятия слов-столбцов. Например, если для рассмотренного шифра взять ключ "РЫБА", то шифрованное сообщение будет выглядеть как "РНМИОИРИТИФАЕЯОЦ".
Системы с ключевым словом или просто ключом, известные с XVI века, широко применяются до сих пор. Их особенностью является два уровня секретности. Первый уровень - это собственно способ составления кода, который постоянно известен лицам, использующим данный шифр. Второй уровень - это ключ, который посылается отдельно от основного сообщения по особо защищенным каналам и без которого расшифровка основного сообщения невозможна.
Наиболее простой способ использования ключа хорошего шифра следующий: под символами сообщения записывается раз за разом ключ, затем номера соответствующих знаков сообщения и ключа складываются. Если полученная сумма больше общего числа знаков, то от нее отнимается это общее число знаков. Полученные числа будут номерами символов кода. С ростом длины ключа трудоемкость дешифровки подобного шифра стремительно растет. Например, рассмотренное ранее сообщение с ключом "КИБЕРНЕТИКА" в шифрованном виде будет выглядеть как "ЮОРЦЪНОБЮЪСШЙШОЪ". Процесс шифровки описывается схемой:
| Т | Е | О | Р | И | Я | И | Н | Ф | О | Р | М | А | Ц | И | И |
| 20 | 6 | 16 | 18 | 10 | 33 | 10 | 15 | 22 | 16 | 18 | 14 | 1 | 24 | 10 | 10 |
| К | И | Б | Е | Р | Н | Е | Т | И | К | А | К | И | Б | Е | Р |
| 12 | 10 | 2 | 6 | 18 | 15 | 6 | 20 | 10 | 12 | 1 | 12 | 10 | 2 | 6 | 18 |
| 32 | 16 | 18 | 24 | 28 | 15 | 16 | 2 | 32 | 28 | 19 | 26 | 11 | 26 | 16 | 28 |
| Ю | О | Р | Ц | Ъ | Н | О | Б | Ю | Ъ | С | Ш | Й | Ш | О | Ъ |
Если в качестве ключа использовать случайную последовательность, то получится нераскрываемый шифр. Проблема этого шифра - это способ передачи ключа.
В информационных сетях использование традиционных систем шифрования с ключом затрудненно необходимостью иметь специальный особо защищенный способ для передачи ключа. В 1976 году У. Диффи (Diffie W.) и М. Хеллман (Hellman M.) - инженеры-электрики из Станфордского университета, а также студент Калифорнийского университета Р. Меркль (Merkle R.), предложили новый принцип построения криптосистем, не требующий передачи ключа принимающему сообщение и сохранения в тайне метода шифрования. В дальнейшем, в качестве примеров, рассмотрим три системы, основанные на идеях Диффи и Хеллмана: без передачи ключей, с открытым ключом и электронную подпись - все они в свою очередь основаны на математическом фундаменте теории чисел.
Упражнение 47 Зашифровать сообщение "КИБЕРНЕТИКА" ключом "ДИСК".
