Графика в Python и задачи моделирования
3.1 Управление исполнителем "черепашка"
Исполнитель "черепашка" управляется командами относительных ("вперёд- назад" и "направо-налево") и абсолютных ("перейти в точку с координатами...") перемещений. Исполнитель представляет собой "перо", оставляющее след на плоскости рисования. Перо можно поднять, тогда при перемещении след оставаться не будет. Кроме того, для пера можно установить толщину и цвет. Все эти функции исполнителя обеспечиваются модулем turtle ("черепаха").
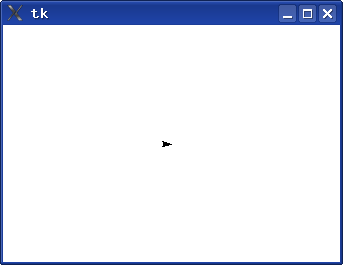
Приведённый ниже код создаёт графическое окно (рис. 3.1) и помещает перо ("черепашку") в исходное положение.
# -*- coding: utf-8 -*-
import turtle
# Инициализация turtle.reset() # Здесь могут быть вычисления и команды рисования # turtle._root.mainloop() # для Python 2.4.x и 2.5.x # Эта команда показывает окно, пока его не закроют turtle.mainloop() # для Python 2.6.x
Как видно из этого примера, способ вызова метода mainloop() для показа графического окна зависит от версии Python. Поэтому если не работает один вариант, смело используйте другой. В остальных примерах будет использоваться вариант для Python 2.6.
Полученное окно имеет фиксированный размер, который зависит от версии Python, перо позиционируется в центре. Идея рисования заключается в перемещении пера ("черепашки") в точки окна рисования с указанными координатами или в указанных направлениях на заданные расстояния, а также в проведении отрезков прямых, дуг и окружностей.
Текущее направление перемещение пера (соответствующее направлению "вперёд") указывается остриём стрелки изображения "черепашки".
Полный список команд управления "черепашкой" (и, соответственно, рисования), а также функций, обеспечиваемых модулем, можно получить, набрав в окне выполнения любой системы программирования на Python команду help('turtle').
Список этот довольно длинный, а среди предоставляемых функций имеются также математические, поскольку они могут быть востребованы при вычислении параметров отрезков, дуг и окружностей.
Команды, обеспечивающие рисование, приведены ниже.
| Команда | Назначение | Пример |
|---|---|---|
| up() | Поднятие "пера", чтобы не оставалось следа его при перемещении | turtle.up() |
| down() | Опускание "пера", чтобы при перемещении оставался след (рисовались линии) | turtle.down() |
| goto(x,y) | Перемещение "пера" в точку с координатами 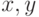 в системе координат окна рисования в системе координат окна рисования |
turtle.goto(50,20) |
| color ('цвет') | Установка цвета "пера" в значение, определяемое строкой цвета |
turtle.color('blue')
turtle.color('#0000ff') |
| width(n) | Установка толщины "пера" в точках экрана | turtle.width(3) |
| forward(n) | Передвижение "вперёд" (в направлении острия стрелки, см. рис. 3.1) на  точек точек |
turtle.forward(100) |
| backward(n) | Передвижение "назад" на n точек | turtle.backward(100) |
| right(k) | Поворот направо (по часовой стрелке) на  единиц единиц |
turtle.right(75) |
| left(k) | Поворот налево (против часовой стрелки) на  единиц единиц |
turtle.left(45) |
| radians () | Установка единиц измерения углов в радианы | turtle.radians() |
| degrees () | Установка единиц измерения углов в градусы (включён по умолчанию) | turtle.degrees() |
| circle(r) | Рисование окружности радиусом 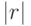 точек из текущей позиции "пера". Если точек из текущей позиции "пера". Если  положительно, окружность рисуется против часовой стрелки, если отрицательно — по часовой стрелке. положительно, окружность рисуется против часовой стрелки, если отрицательно — по часовой стрелке. |
turtle.circle(40) turtle.circle(-50) |
| circle(r,k) | Рисование дуги радиусом 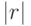 точек и углом точек и углом  единиц. Вариант команды circle() единиц. Вариант команды circle()
|
turtle.circle(40,45) turtle.circle(-50,275) |
| fill (flag) | В зависимости от значения flag включается (flag=1) и выключается (flag=0) режим закрашивания областей. По умолчанию выключен. | Круг:
turtle.fill(1) turtle.circle(-50) turtle.fill(0) |
| write ('строка') | Вывод текста в текущей позиции пера | turtle.write('Начало координат!') |
| tracer(flag) | Включение (flag=1) и выключение (flag=0) режима отображения указателя "пера" ("черепашки"). По умолчанию включён. | turtle.tracer(0) |
| clear() | Очистка области рисования | turtle.clear(0) |
При выключенном режиме отображения указателя "черепашки" рисование происходит значительно быстрее, чем при включённом.
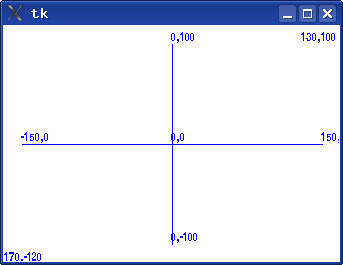
Проделаем упражнение с целью определить систему координат окна рисования. Приведённый ниже код формирует картинку, показанную на рис. 3.2.
# -*- coding: utf-8 -*-
import turtle
#
turtle.reset()
turtle.tracer(0)
turtle.color('#0000ff')
#
turtle.write('0,0')
#
turtle.up()
x=-170
y=-120
coords=str(x)+","+str(y)
turtle.goto(x, y)
turtle.write(coords)
#
x=130
y=100
coords=str(x)+","+str(y)
turtle.goto(x, y)
turtle.write(coords)
#
x=0
y=-100
coords=str(x)+","+str(y)
turtle.goto(x, y)
turtle.write(coords)
#
turtle.down()
x=0
y=100
coords=str(x)+","+str(y)
turtle.goto(x, y)
turtle.write(coords)
#
turtle.up()
x=-150
y=0
coords=str(x)+","+str(y)
turtle.goto(x, y)
turtle.write(coords)
#
turtle.down()
x=150
y=0
coords=str(x)+","+str(y)
turtle.goto(x, y)
turtle.write(coords)
#
turtle.mainloop()Здесь строка с координатами формируется "в лоб", путём конкатенации преобразованных в строки значений координат.
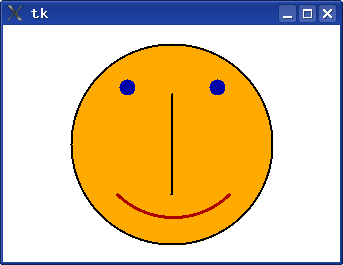
Картинка, показанная на рис. 3.3, сформирована нижеследующим кодом.
# -*- coding: utf-8 -*-
import turtle
#
turtle.reset()
turtle.tracer(0)
turtle.width(2)
#
turtle.up()
x=0
y=-100
turtle.goto(x, y)
turtle.fill(1)
turtle.color('#ffaa00')
turtle.down()
turtle.circle(100)
turtle.fill(0)
turtle.color('black')
turtle.circle(100)
turtle.up()
#
x=-45
y=50
turtle.goto(x, y)
turtle.down()
turtle.color('#0000aa')
turtle.fill(1)
turtle.circle(7)
turtle.up()
turtle.fill(0)
#
x=45
y=50
turtle.goto(x, y)
turtle.down()
turtle.color('#0000aa')
turtle.fill(1)
turtle.circle(7)
turtle.up()
turtle.fill(0)
#
x=-55
y=-50
turtle.goto(x, y)
turtle.right(4 5)
turtle.width(3)
turtle.down()
turtle.color('#aa0000')
turtle.circle(80, 90)
turtle.up()
#
turtle.right(135)
x=0
y=50
turtle.goto(x, y)
turtle.width(2)
turtle.color('black')
turtle.down()
turtle.forward(100)
#
turtle.mainloop()Для того, чтобы изобразить улыбку, потребовалось после перемещения пера в начальную точку дуги (левую) повернуть перо на 45 градусов. Дело в том, что изначально направлением "вперёд" для пера является направление вправо (как показано на рис. 3.1). Окружности и дуги рисуются как касательные к этому "вектору", начинаясь в точке с текущими координатами пера. Поэтому для улыбки потребовалось изменить направление "вектора".
Далее, перо, первоначально сориентированное на 45 градусов вправо, после прохождения дуги в 90 градусов соответственно изменило своё направление. Поэтому для получения вертикальной линии его пришлось дополнительно повернуть.
Можно поэкспериментировать с рисованием домиков, солнышка и более сложных композиций. Однако для формирования сложных кривых (например, графиков функций) с помощью этого модуля придётся многократно выполнять команду goto(x,y). В этом легко убедиться, попытавшись нарисовать, например, график параболы.
3.1.1 Задания и упражнения
- Как в примерах кода, формирующего изображения на рис. 3.2 и рис. 3.3, применить кортежи?
- Напишите код для создания изображения "домика" (квадрат под треугольником) без подъёма пера при условии однократного перемещения по каждой линии.
- Рассчитайте координаты и напишите код для создания изображения "солнца" (круг и расходящиеся от него отрезки) так, чтобы "лучи" начинались на расстоянии 2 точки от круга (не менее 8-ми лучей).
- Напишите код для построения графика степенной функции (
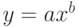 ) с началом координат в левой нижней четверти окна рисования так, чтобы кривая проходила практически через всё окно.
) с началом координат в левой нижней четверти окна рисования так, чтобы кривая проходила практически через всё окно.