Программирование на кластерах с использованием инструментов Intel (Intel Cluster Studio)
[+]
Опубликован: 11.10.2012 | Доступ: платный | Студентов: 5 / 2 | Длительность: 07:36:00
Темы: Программирование, Суперкомпьютерные технологии
Специальности: Программист, Системный архитектор
Теги: mpi, кластеры, распараллеливание, распределенные вычисления, суперкомпьютеры
Самостоятельная работа 7:

Распараллеливание программы решения систем линейных алгебраических уравнений методом Гаусса с помощью OpenMP и MPI
A
|
версия для печати
< Самостоятельная работа 6 || Самостоятельная работа 7 || Самостоятельная работа 8 >
Ключевые слова: программа, Профилирование, цикла, параметр, инвариант, операция приведения, ПО, предсказуемость, объединение, расходы, запуск, трансляция, транслятор, ключ, матрица, вектор, метод Гаусса, погрешность, вычисление, распараллеливание, MPI

Распараллеливание программ с помощью OpenMP

Параллельная OpenMP-программа состоит из последовательных и параллельных секций. Границы параллельных секций обозначаются директивами OpenMP. Процесс разработки OpenMP-программы включает следующие этапы:

  • Разработка последовательной программы.
  • Выявление участков потенциального параллелизма. Чаще всего это циклы.
  • Анализ трудоемкости параллельных секций (профилирование программы). Наибольший выигрыш в производительности дает распараллеливание секций, на которые приходятся наибольшие затраты процессорного времени.
  • Пошаговое распараллеливание программы, начиная с наиболее трудоемких секций.

Профилирование может производиться как с помощью специальных программных инструментов, так и простыми средствами, например, с помощью вызова специальных подпрограмм-таймеров, размещенных в различных местах программы.

Цикл эффективно распараллеливается, если отсутствуют перекрестные зависимости между его итерациями. Избавиться от таких зависимостей иногда можно, выполнив преобразование цикла.

Необходимо правильно определить область видимости переменных в параллельных секциях программы. Параметр цикла, например, должен быть объявлен локальной переменной. Инвариант цикла (величина, не изменяющаяся при выполнении итераций цикла) должен быть глобальным.

При вычислении суммы, например, к переменной, которая используется для "накопления" суммы, должна быть применена операция приведения (редукции).

Следует обратить внимание на синхронизацию вычислений. По умолчанию в циклах используется барьерная синхронизация. Наличие синхронизаций увеличивает предсказуемость поведения программы, но замедляет ее работу.

Дополнительный выигрыш в производительности дает объединение нескольких параллельных секций в одну. В этом случае уменьшаются накладные расходы на запуск нитей и их завершение.

Трансляция OpenMP-программ

Трансляция OpenMP-программы выполняется со специальным ключом. В операционной системе Linux транслятор Intel®Compiler использует ключ –openmp, например:

#ifort –o my_prog prog_source.f90 -openmp

В операционной системе Microsoft®Windows командная строка выглядит следующим образом:

#ifort prog_source.f90 /Qopenmp

Решение систем линейных алгебраических уравнений методом Гаусса

Классическим численным методом решения систем линейных алгебраических уравнений:

Ax=b,

где 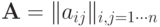$\mathbf{A}=\|a_{ij}\|_{i,j=1\cdots n}$ - квадратная матрица коэффициентов, x - вектор неизвестных, а

b - вектор правой части, является метод Гаусса. Он относится к числу "точных" методов, то есть погрешность метода Гаусса определяется только погрешностью машинной арифметики. "Точные" методы решения систем линейных алгебраических уравнений основаны, как правило, на преобразовании исходной задачи к такой эквивалентной (имеющей то же решение), которая допускала бы простое вычисление компонентов вектора неизвестных. Это может быть система с диагональной или, как в методе Гаусса, треугольной матрицей коэффициентов. Переход к системе с верхней треугольной матрицей производится путем линейного комбинирования строк. Решение системы при этом не изменяется.

Приведем описание алгоритма для метода Гаусса.

Прямой ход

  1. Найти наибольший по абсолютной величине элемент первого столбца и поменять соответствующую строку местами с первой.
  2. Выбирая подходящим образом множители для элементов первой строки и складывая полученные произведения с элементами строк со 2-й по n-ю, обратить в ноль все элементы первого столбца, находящиеся ниже главной диагонали. При вычислении комбинаций следует учитывать и вектор правой части.
  3. Повторить данную процедуру для второй строки и второго столбца и т. д.

Обратный ход (обратная подстановка)

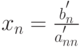  1. Вычислить $x_{n}=\frac{b^{'}_{n}}{a^{'}_{nn}}$.
  2. Для i=n-1,...,1 вычислить $x_i=\frac{1}{a^{'}_{ii}}\Bigl (b^{'}_{i}-\sum^{n}_{j=i+1}a^{'}_{ij}x_j\Bigr)$.

Очевидным условием применимости метода Гаусса в его простейшей формулировке, приведенной выше, является отсутствие нулевых элементов на главной диагонали матрицы коэффициентов, в противном случае возникает опасность аварийного завершения программы при делении на ноль. По этой причине в реальных расчетах используются более сложные модификации метода Гаусса.

Лабораторная работа

В заданиях лабораторной работы 2.1 предлагается выполнить распараллеливание последовательной программы, предназначенной для решения систем линейных алгебраических уравнений. В задании 4 распараллеливание производится с помощью MPICH 1.2.7. Цель работы – получить навык анализа программ, выявления в них участков потенциального параллелизма с наибольшей трудоемкостью, применить для распараллеливания OpenMP и MPI, сравнить трудоемкость обоих подходов и эффективность полученного результата. Звездочкой отмечено задание повышенной сложности.

Необходимый для выполнения данной лабораторной работы справочный материал можно найти на стр. 13 – 24 методического пособия "Средства программирования для многопроцессорных вычислительных систем".

Задания для практической работы

Задание 1

Получить у преподавателя файл с исходным текстом программы (пример 1) и ознакомиться с реализацией простого метода Гаусса.

Задание 2

Откомпилировать программу, выполнить расчет. Определить процессорное время, потраченное на выполнение расчета.

Задание 3

Проанализировать последовательный код. Выявить участки потенциального параллелизма с наибольшей трудоемкостью. Для этого следует подсчитать количество операций для прямого хода метода Гаусса и хода обратной подстановки. Выполнить распараллеливание с помощью OpenMP. Определить процессорное время, потраченное на выполнение расчета для разного числа потоков (меньшего, равного и большего, чем число процессоров). Сравнить с результатом, полученным в задании 2. Объяснить полученный результат.

Задание 4*

Распараллелить программу с помощью MPI. Определить процессорное время, потраченное на выполнение расчета. Сравнить с результатами, полученными в заданиях 2 и 3.

Задание 5

На основании результатов, полученных при выполнении заданий данной лабораторной работы, написать отчет, в котором содержатся выводы об эффективности различных способов распараллеливания исходного последовательного кода и трудоемкости реализации этих способов на практике.

Пример 1

В программе на языке Fortran 90 реализован простой метод Гаусса без выбора ведущего элемента. 

program linear_algebra_gauss 
 
integer, parameter :: n = 3 
real, dimension(1:n, 1:n) :: a, left 
real, dimension(1:n) :: x, b  
 
data left/9 * 0./ 
data a/ .471, 4.27, .012, 3.21, -.513, 1.273, -1.307, 1.102, -
4.175 / 
data b/ 2.425, -.176, 1.423 / 
! Решение: 0.07535443 0.6915624 -0.1297573 
 
! Прямой ход метода Гаусса 
 
do k = 1, n - 1 
 do i = k + 1, n 
  left(i, k) = a(i, k) / a(k, k) 
  b(i) = b(i) - left(i, k) * b(k) 
 end do 
 do j = k + 1, n 
  do i = k + 1, n 
 
  a(j, i) = a(j, i) - left(j, k) * a(k, i) 
  end do 
 
 end do 
end do 
 
! Обратная подстановка
x(n) = b(n) / a(n, n) 
 
do i = n - 1, 1, -1 
 x(i) = b(i) 
 do j = i + 1, n 
  x(i) = x(i) - a(i, j) * x(j) 
 end do 
 x(i) = x(i) / a(i, i) 
end do 
 
print *, (x(i), i = 1, n) 
 
end
Дальше >>
< Самостоятельная работа 6 || Самостоятельная работа 7 || Самостоятельная работа 8 >

Вопросы и ответы

вопросов: 0