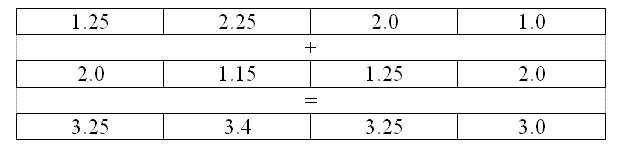|
Здравствуйие! Я хочу пройти курс Введение в принципы функционирования и применения современных мультиядерных архитектур (на примере Intel Xeon Phi), в презентации самостоятельной работы №1 указаны логин и пароль для доступ на кластер и выполнения самостоятельных работ, но войти по такой паре логин-пароль не получается. Как предполагается выполнение самосоятельных работ в этом курсе? |
Векторные расширения Intel Xeon Phi
Введение
Презентацию к лекции Вы можете скачать здесь.
Начиная с середины XX века, программирование проделало большой путь и постоянно продолжает развиваться. Вспомним не такие уж далекие времена, когда наши коллеги писали свои программы в машинных кодах, непосредственно работая со справочником, содержащим информацию о поддерживаемом в процессоре наборе команд. Сейчас уже трудно представить, что в стиле "3E; 24; 5F…" можно написать сколько-нибудь серьезную программу, а ведь когда-то это было реальностью. В 1992 году в 10 классе школы одноклассник автора данной лекции самостоятельно, без чьей-либо помощи, кроме, быть может, моральной, написал в машинных кодах среду программирования с текстовым редактором и транслятором языка BASIC для ПК "Корвет". В то же время Ваш покорный слуга и его друзья-школьники по обрывочным, перепечатанным много раз брошюрам осваивали и применяли на практике язык Ассемблер для ПК "ZX SPECTRUM", построенного на базе восьмиразрядного процессора Z80. Да, в то время тоже можно было писать на BASIC и других высокоуровневых языках, но в этом случае быстродействие программ оставляло желать лучшего, а доступ к ряду возможностей процессора был закрыт вовсе. В наши времена программирование в машинных кодах практически стало историей, а разработка программ на ассемблере имеет смысл в весьма ограниченном числе случаев. Одна из причин этого – невероятно возросший интеллект компиляторов языков высокого уровня C, C++, Fortran, ориентированных на высокопроизводительные вычисления (high performance computing, HPC). Ни на миг не отвлекаясь от главной задачи – генерации корректного кода, оптимизирующие компиляторы умудряются выполнять многочисленные эквивалентные (точно или с точностью до разрешенных отклонений, например, при изменении порядка операций с плавающей запятой) преобразования, изменяя наш код до неузнаваемости и обеспечивая производительность, часто сопоставимую с хорошей программой на ассемблере. Отметим, что оптимизирующие компиляторы (в частности, одни из лучших представителей данной группы – Intel C/C++ Comiler, Intel Fortran Compiler) умеют использовать новые наборы команд и генерировать код, ориентированный на современные центральные процессоры.
Остановимся на данном аспекте подробнее. Что значит "код, ориентированный на современные центральные процессоры"? Важный момент состоит в использовании новых команд и наборов команд, добавленных в процессор его производителем. Чтобы понять, почему это важно, обсудим возможные перспективы расширения функциональности процессора в результате добавления новых команд. Первая мысль, которая приходит в голову, звучит так: почему бы инженерам не поместить в набор команд часто используемые в научных и инженерных приложениях, составляющих основу области HPC, вычисление математических функций (sin, cos, exp, pow, …), генератор случайных чисел и многие другие полезные возможности? К сожалению, аппаратная реализация подобных "команд" весьма сложна и требует добавления значительного числа дополнительных транзисторов, что приведет к неприемлемому увеличению размера, энергопотребления и стоимости процессора. Таким образом, любое расширение набора команд является важным событием, не остается незамеченным в индустрии и быстро "подхватывается" разработчиками компиляторов. Действительно, раз уж несмотря на все трудности создатели процессора смогли добавить дополнительные команды, имеет смысл предоставить доступ к ним широкому кругу разработчиков ПО, использующих языки программирования высокого уровня.
Данная лекция рассматривает одно из важных направлений развития наборов команд в рамках современных архитектур – векторные расширения. Что такое векторные расширения? Это дополнение в набор команд процессора, содержащее специализированные типы данных, регистры и инструкции, ориентированные на использование парадигмы SIMD – Single Instruction Multiple Data. Суть парадигмы SIMD заключается в выполнении одной командой однотипных операций над пакетом данных. При этом реализуется один из видов параллельной обработки данных, что открывает возможность существенного повышения производительности вычислительных программ. Разумеется, не во всех практических приложениях векторизация – использование векторных инструкций – позволяет добиться существенного прироста производительности. Казалось бы – все просто. Пусть мы обрабатываем числа двойной точности, имеем специальные регистры, позволяющие хранить по 4 таких числа, а также арифметические команды, позволяющие векторно выполнять операции ( рис. 4.1).
На первый взгляд, мы можем ожидать ускорение вычислений до четырех раз по сравнению с обычным (скалярным) кодом. Однако на практике этого зачастую не происходит. Во-первых, присутствуют определенные накладные расходы на упаковку данных в регистры и распаковку результатов расчета. В наилучшем случае мы можем загрузить/выгрузить данные одной командой. Для этого необходимо, чтобы данные лежали в памяти последовательно или (для некоторых векторных расширений) с определенным шагом. В последнем случае надо учитывать и эффективность использования особенностей иерархической организации подсистемы памяти. Во-вторых, может так случиться, что есть зависимость между значениями элементов векторов и некоторых результатов расчета – зависимости по данным, что делает невозможным параллельное выполнение операций. В связи с этим в некоторых случаях мы можем наблюдать, что несмотря на наши усилия компилятор отказывается генерировать векторный код, а иногда нам удается его уговорить, но мы не получаем осязаемого выигрыша во времени.
Тем не менее, спектр алгоритмов, для которых векторизация соответствующего программного кода является одним из важных ресурсов повышения производительности, является достаточно большим. Так, для мультимедийных приложений характерно применение алгоритмов, многократно повторяющих однотипные операции над большими массивами данных. При выполнении инженерных расчетов во многих случаях удается успешно векторизовать хотя бы часть программы и получить выигрыш в производительности. Отметим также, что в современных центральных процессорах размер вектора в случае вычислений с одинарной точностью составляет 4 (наборы инструкций SSE) и 8 (набор инструкций AVX), а для вычислений с двойной точностью – 2 (наборы инструкций SSE) и 4 (набор инструкций AVX). Таким образом, избегая векторизации расчетных частей алгоритма, мы теряем до 87,5% производительности, что весьма существенно. В случае использования Xeon Phi мы можем констатировать еще больший вклад векторизации в общую производительность программы, поскольку размер вектора увеличился вдвое по сравнению с AVX. Таким образом, как на традиционных процессорах, так и, тем более, на ускорителях Xeon Phi умелое использование векторных расширений является одним из ключевых механизмов, влияющих на производительность программы.
Дальнейшее изложение материала о векторизации построено следующим образом. В данной лекции дается общее описание векторных расширений в Intel Xeon Phi и подходы к их использованию в программах на языках C/C++. В лекции №5 рассматриваются более "тонкие" особенности использования указанных расширений при написании прикладных программ на языках высокого уровня с использованием возможностей компиляторов Intel. Техника применения векторных вычислений формируется в " Оптимизация расчетов на примере задачи вычисления справедливой цены опциона Европейского типа " , на примерах иллюстрирующей некоторые типовые проблемы векторизации кода и методы их решения. В дальнейших практических работах векторизация неизменно упоминается и применяется в качестве одного из ключевых способов повышения производительности программ.
Векторные расширения. Краткий обзор
В настоящее время векторные расширения присутствуют в наборах команд процессоров различных производителей и архитектур. Так, в центральных процессорах Intel соответствующие наборы команд эволюционировали по пути MMX – SSE – SSE2 – SSE3 – SSE4 – AVX, преодолев путь от векторной целочисленной арифметики, организованной на специализированных 64-разрядных регистрах, и ориентированной преимущественно на обработку звука и видео, до широкого спектра арифметических операций с плавающей запятой, работающей на 256-разрядных регистрах, и операций управления работой подсистемы памяти. Рассматривая векторные расширения, необходимо упомянуть дополнение 3DNow!, реализованное в процессорах AMD, а также расширение NEON, активно развивающееся в процессорах архитектуры ARM, широко распространенных во встраиваемых системах. Рассмотрим кратко векторные расширения, реализованные в Intel Xeon Phi. Данное описание не претендует на полноту. Оно призвано составить общее впечатление о сути вопроса для лучшего понимания того, как соотносится расчетный код на C/C++ и машинный/ассемблерный коды, порождаемые компилятором. Данное понимание весьма полезно при оптимизации программ по скорости их работы. Желающие познакомиться с вопросом в большем объеме могут обратиться к источникам [4.1] и [4.3].
Типы данных и регистровый пул
В ядрах ускорителей Intel Xeon Phi сделан следующий шаг в развитии векторных расширений набора команд. Так, уже привычные для программистов MMX, SSE, AVX не поддерживаются. Однако вместо этого в каждом ядре сконструирован специальный модуль векторной обработки (VPU, vector processor unit), содержащий 32 512-разрядных регистра (zmm-регистры; отметим двукратное увеличение размера регистра по сравнению с AVX) и открывающий новые возможности по обработке данных с использованием векторных инструкций вида 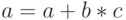 с однократным округлением (FMA, fused multiply–add), а также некоторых других возможностей.
с однократным округлением (FMA, fused multiply–add), а также некоторых других возможностей.
Итак, учитывая размер векторного регистра, на каждом ядре Intel Xeon Phi мы можем одновременно производить действия над 16 32-битными целыми числами или 8 64-битными целыми числами или 16 числами с плавающей запятой одинарной точности или 8 числами с плавающей запятой двойной точности. Кроме того, поддерживаются операции с комплексными данными. Заметим, что в отличие от привычных наборов команд в векторных расширениях Intel Xeon Phi большинство операций являются тернарными – имеют 2 аргумента и один результат, что по некоторым данным (см., например, [4.1]), приводит к 20% росту производительности по сравнению с традиционной схемой работы, основанной на двух операндах. Для FMA все три операнда являются аргументами, при этом один из них в то же время принимает результат.
Обзор основных типов операций
Поддерживаются следующие основные операции:
- Арифметические операции: сложение, вычитание, умножение, деление, FMA (для вычислений с плавающей запятой).
- Операции преобразования типов, позволяющие выполнять повышающие и понижающие преобразования согласно определенным правилам (см. [4.1],[4.3]).
- Логические операции, позволяющие выполнять векторные сравнения, находить минимум и максимум и т.д.
- Операции доступа к данным. В эту группу входят команды загрузки данных из памяти в регистр и выгрузки данных из регистра в память. В новом наборе команд поддерживаются так называемые scatter/gather-инструкции, позволяющие оперировать с данными, хранящимися в памяти с пропусками с определенным шагом. Также реализованы команды предвыборки данных, позволяющие выполнять упреждающую загрузку в кэш-память. Важно отметить, что выравнивание данных в памяти существенно влияет на производительность. Этот вопрос будет подробно рассмотрен позже. При выполнении операций доступа к данным может быть указано, что с точки зрения программиста те или иные данные не имеет смысла кешировать (nontemporal data). Для оптимизации кода с учетом этого факта при записи в память результатов вычислений, идентифицированных нами как nontemporal data, предназначены так называемые streaming stores, использование которых приводит к уменьшению накладных расходов.
Также реализованы следующие возможности:
- При выполнении операций может применяться маскирование: при помощи специального регистра может быть указано, над какой частью регистра-операнда выполнять операцию. По умолчанию такой специальный регистр содержит все единицы, а операции выполняются над всеми операндами.
- При выполнении операций может производиться перестановка/размножение частей операндов при помощи соответствующих модификаторов (swizzle). Аналогичные манипуляции могут выполняться, когда один из аргументов указывает на данные в оперативной памяти (broadcast). Еще большими возможностями по перестановкам обладает т.н. "смешивание" (shuffle), обладающее неограниченными возможностями по перемещению байтов в регистре.
Расширенная поддержка математических функций
В рамках Intel Xeon Phi была реализована расширенная поддержка некоторых математических функций. Так, появились команды для вычисления в одинарной точности функций 1/x, 1/sqrt(x), log2(x), 2x. Первые три инструкции имеют латентность 4 такта и пропускную способность 1 такт, последняя – латентность 8 тактов и пропускную способность 2 такта. Нетрудно видеть, что sqrt(x), ax и деление могут быть вычислены при помощи указанных функций. Вопрос о векторизации циклов, содержащих вызовы математических функций, будет рассмотрен позже.