Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений
8.1. Базовые понятия
Рассмотрим численные методы решения задачи Коши для обыкновенных дифференциальных уравнений (ОДУ) вида
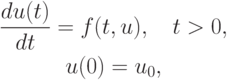 |
( 8.1) |
а также систем ОДУ
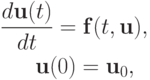
где
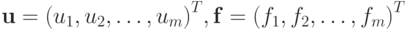
- векторы столбцы искомых функций и правых частей соответственно.
К аналогичной форме приводится задача Коши для обыкновенного дифференциального уравнения (системы уравнений) порядка выше первого, вида
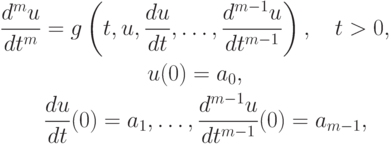
если положить

Введем в расчетной области ![t \in \left[{0, T}\right]](/sites/default/files/tex_cache/d5a3096ae7ff038eaa62fffde6d55014.png) точки (узлы расчетной сетки)
точки (узлы расчетной сетки)  в которых вычисляется искомое решение. Совокупность узлов называется расчетной сеткой, (сеточной областью),
в которых вычисляется искомое решение. Совокупность узлов называется расчетной сеткой, (сеточной областью),  — шагом интегрирования. Здесь для простоты введена равномерная сетка.
В реальных расчетах применяются и неравномерные сетки.
— шагом интегрирования. Здесь для простоты введена равномерная сетка.
В реальных расчетах применяются и неравномерные сетки.
Введем сеточную функцию 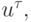 определенную в узлах сетки и
представляющую собой совокупность приближенных значений искомой функции,
определенную в узлах сетки и
представляющую собой совокупность приближенных значений искомой функции, 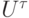 — проекцию точного решения искомой задачи на сетку и
— проекцию точного решения искомой задачи на сетку и 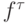 — значения правой части в узлах сетки.
— значения правой части в узлах сетки.
Введем вслед за [8.1] также операторное обозначение дифференциальной задачи
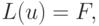 |
( 8.2) |
где
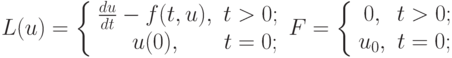
и аппроксимирующей разностной задачи
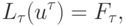 |
( 8.3) |
где  — обозначения разностного оператора,
— обозначения разностного оператора,  — проекция F на
расчетную сетку. Заметим, что u и
— проекция F на
расчетную сетку. Заметим, что u и 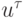 являются элементами соответственно функционального и конечномерного пространств. Определим основные понятия теории разностных схем [8.1], [8.2].
являются элементами соответственно функционального и конечномерного пространств. Определим основные понятия теории разностных схем [8.1], [8.2].
Определение. Решение задачи (8.3) 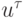 сходится при
сходится при  к решению исходной задачи (8.2), если
к решению исходной задачи (8.2), если

при 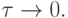
При этом, если имеет место оценка
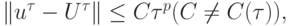
то имеет место сходимость порядка p.
Определение. Говорят, что задача (8.3) аппроксимирует задачу (8.2) на ее решении, если невязка

при  где
где 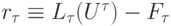 ; при этом, если имеет место оценка
; при этом, если имеет место оценка
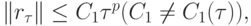
то говорят, что имеет место аппроксимация порядка p.
Определение. Задача (8.3) устойчива, если из соотношений
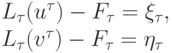
следует

Теорема 1 (В.С.Рябенького - П. Лакса). Решение задачи (8.3) сходится к решению исходной задачи (8.2), если задача (8.3) устойчива и аппроксимирует задачу (8.2); если аппроксимация имеет порядок p, то сходимость также имеет порядок p.
Доказательство.
В силу аппроксимации имеем оценку:  Тогда из определения устойчивости, положив
Тогда из определения устойчивости, положив 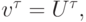 получим
получим

поскольку в данном случае
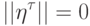
и, кроме того,

Приведем примеры простейших разностных уравнений, аппроксимирующих (8.1):
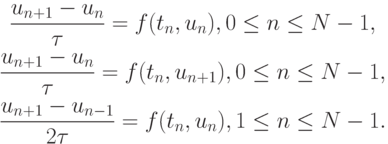
Первая из схем называется явной (явная схема Эйлера), вторая — неявной (неявная схема Эйлера). Алгоритмическая реализация первой схемы — бегущий счет (рекуррентная формула), второй — решение нелинейного алгебраического уравнения на каждом временном шаге.
Для реализации третьей схемы необходимо задание функции un в двух точках: t0 и t1 . Один из возможных вариантов — решение на первом шаге нелинейного уравнения вида:
![$
\frac{u_{n + 1} - u_{n - 1}}{2{\tau}} = \frac{1}{2} [f(t_{n - 1}, u_{n - 1}) + f(t_{n + 1}, u_{n + 1})] $](/sites/default/files/tex_cache/1e6c85a1c977f5b85507cbd1e814a2d3.png)
при n = 1.
В данном случае проявляется несовпадение формальных порядков дифференциального и разностного уравнений (дифференциальное уравнение первого порядка, разностное — второго).
Один из первых методов приближенного решения обыкновенных дифференциальных уравнений — разложение в ряд Тейлора.
Дифференцируя по t исходное уравнение (8.1), получим
u'' = f't(t, u) + f't(t, u) u', u''' = f''tt(t, u) + 2f''tu(t, u) u' + f''uu(t, u) (u')2 + f'u(t, u) u'', ...
