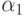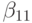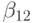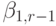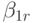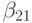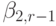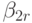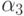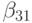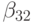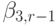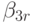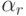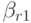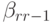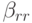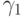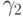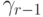НОУ ИНТУИТ | Введение в вычислительную математику. Лекция 9: Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 25.10.2007 | Уровень: специалист | Доступ: свободно | ВУЗ: Московский физико-технический институт

|

Вам нравится? Нравится 54 студентам

| Поделиться |

Поддержать программу

Общие условия аппроксимации методов Рунге - Кутты и барьеры Бутчера. Вернемся к общей записи метода Рунге - Кутты (8.4) и соответствующей таблице Бутчера. Рассматривается задача

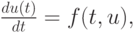
$\frac{d {u}(t)}{d t} = f(t, u),$

u(0) = u₀,

а численный метод имеет вид

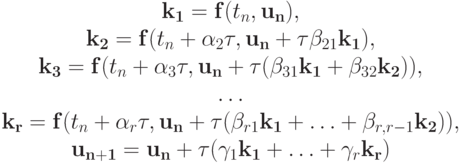
$\left. \begin{array}{c} \mathbf{k_1} = \mathbf{f}(t_n, \mathbf{u_n}), \\ \mathbf{k_2} = \mathbf{f}(t_n + \alpha_2{\tau}, \mathbf{u_n} + {\tau}\beta_{21}\mathbf{k_1}), \\ \mathbf{k_3} = \mathbf{f}(t_n + \alpha_3{\tau}, \mathbf{u_n} + {\tau}(\beta_{31}\mathbf{k_1} + \beta_{32}\mathbf{k_2})), \\ \ldots \\ \mathbf{k_r} = \mathbf{f}(t_n + \alpha_r{\tau}, \mathbf{u_n} + {\tau}(\beta_{r1}\mathbf{k_1} + \ldots + \beta_{r, r - 1}\mathbf{k_2})), \\ \mathbf{u_{n + 1}} = \mathbf{u_n} + {\tau}(\gamma_1\mathbf{k_1} + \ldots + \gamma_r\mathbf{k_r}) \end{array} \right.$

где k_i — вспомогательные векторы.

Наряду с явными, рассмотрим также неявные методы Рунге - Кутты, определенные как

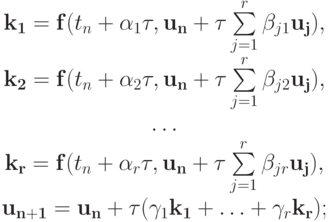
$\left. \begin{array}{c} \mathbf{k_1} = \mathbf{f}(t_n + \alpha_1{\tau}, \mathbf{u_n} + {\tau}\sum\limits_{j = 1}^{r}\beta_{j1}\mathbf{u_j}), \\ \mathbf{k_2} = \mathbf{f}(t_n + \alpha_2{\tau}, \mathbf{u_n} + {\tau}\sum\limits_{j = 1}^{r}\beta_{j2}\mathbf{u_j}), \\ \ldots \\ \mathbf{k_r} = \mathbf{f}(t_n + \alpha_r{\tau}, \mathbf{u_n} + {\tau}\sum\limits_{j = 1}^{r}\beta_{j{r}}\mathbf{u_j}), \\ \mathbf{u_{n + 1}} = \mathbf{u_n} + {\tau}(\gamma_1\mathbf{k_1} + \ldots + \gamma_r\mathbf{k_r}); \end{array} \right.$

таблица Бутчера для неявных методов примет вид

$\alpha_1$	$\beta_{11}$	$\beta_{12}$	$\ldots$	$\beta_{1, r - 1}$	$\beta_{1r}$
$\alpha_2$	$\beta_{21}$	$\beta_{21}$	$\ldots$	$\beta_{2, r - 1}$	$\beta_{2r}$
$\alpha_3$	$\beta_{31}$	$\beta_{32}$	$\ldots$	$\beta_{3, r - 1}$	$\beta_{3r}$$
$\ldots$	$\ldots$	$\ldots$	$\ldots$	$\ldots$	$\ldots$
$\alpha_r$	$\beta_{r1}$	$\beta_{r2}$	$\ldots$	$\beta_{rr - 1}$	$\beta_{rr}$
	$\gamma_1$	$\gamma_2$	$\ldots$	$\gamma_{r - 1}$	$\gamma_r$

Для вывода условий аппроксимации общего метода Рунге - Кутты необходимо действовать так же, как описано выше. Для этого введем погрешность

$\xi ({\tau}) = u(t + {\tau}) - \left[{u(t) + \sum\limits_{j = 0}^{r}{\gamma_j k_j} }\right]$

и представим ее в виде разложения в ряд Маклорена. Приравнивая члены при одинаковых степенях шага 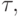$\tau,$ получим условия аппроксимации метода. Для того чтобы метод имел порядок 3, необходимо выполнение следующих условий:

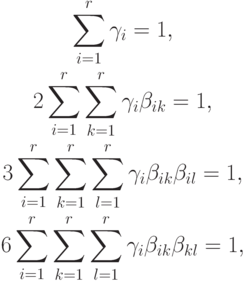
$\begin{gather*} \sum\limits_{i = 1}^{r}{\gamma_i = 1, }\\ 2\sum\limits_{i = 1}^{r}{\sum\limits_{k = 1}^{r}{\gamma_i \beta_{ik}} } = 1, \\ 3\sum\limits_{i = 1}^{r}{\sum\limits_{k = 1}^{r}{\sum\limits_{l = 1}^{r}{\gamma_i \beta_{ik} \beta_{il}} }} = 1, \\ 6\sum\limits_{i = 1}^{r}{\sum\limits_{k = 1}^{r}{\sum\limits_{l = 1}^{r}{\gamma_i \beta_{ik} \beta_{kl}} }} = 1, \end{gather*}$

причем эти выражения упрощаются, если воспользоваться необязательными условиями Кутты. При повышении порядка аппроксимации метода возникают дополнительные условия на коэффициенты, система значительно усложняется.

Для того чтобы построить аппроксимирующую схему ( метод Рунге - Кутты ) необходимо найти набор коэффициентов метода. Как было показано выше, в случае двух стадий метода такой набор коэффициентов — не единственный, существует континуум методов второго порядка аппроксимации. Континуум решений система уравнений порядка для явных методов Рунге - Кутты имеет и в случае явных методов с тремя или четырьмя стадиями. Но для пятистадийного метода система уравнений порядка является несовместной. Это утверждение было доказано Бутчером и носит название "первый барьер Бутчера". Его обычно формулируют в виде теоремы [8.3].

Теорема (первый барьер Бутчера.) Среди явных методов Рунге - Кутты с числом стадий пять не существует методов пятого порядка аппроксимации.

Для повышения порядка до пятого приходится использовать шестистадийные методы. При увеличении числа стадий возникает второй барьер Бутчера — порядок аппроксимации метода, начиная с семи стадий, оказывается уже на 2 ниже, чем число стадий. При увеличении порядка аппроксимации метода приходится значительно увеличивать число стадий — барьеры Бутчера встречаются чаще.

Наличие такого барьера — одно из следствий быстрого роста констант Лебега при интерполяции на равномерной сетке. Дело в том, что явные методы Рунге - Кутты тесно связаны с квадратурными формулами интерполяционного типа. Достаточно очевидно, что классический метод Рунге - Кутты порядка 4 основан на применении формулы Симпсона, а правило 3/8 — на одноименной квадратурной формуле. Как было показано в "Численное интегрирование" , с повышением порядка аппроксимации квадратурные формулы перестают быть правильными, а это следствие роста константы Лебега. Тогда и появляются барьеры Бутчера при построении методов решения систем ОДУ.

От этого недостатка свободны некоторые неявные методы, основанные на квадратурных формулах Гаусса.

Дальше >>

Авторизоваться

Введение в вычислительную математику

Численные методы решения задачи Коши для систем обыкновенных дифференциальных уравнений

Вопросы и ответы