|
Пришлите пожалуйста на почту мне pdf - версию сертификата. |
Основы общей теории измерений
2.1. Измерение, классификация измерений
Основополагающим понятием метрологии является измерение - нахождение значения физической величины опытным путем с помощью специальных технических средств.
Измерение физической величины производят путем ее сравнения в процессе эксперимента с величиной, принятой за единицу физической величины. Целью измерения является получение значения физической величины в наиболее удобной форме. С помощью измерительного прибора определяют, во сколько раз значение данной величины больше или меньше значения величины, принятого за единицу.
Измерения могут быть классифицированы:
- по характеристике точности - равноточные, неравноточные;
- по числу наблюдений - однократные, многократные;
- по режиму работы применяемых средств измерений - статические, динамические;
- по метрологическому назначению - технические, метрологические;
- по выражению результата измерения - абсолютные, относительные;
- по способу обработки экспериментальных данных - прямые, косвенные, совместные, совокупные;
- по способу применения меры - методом непосредственной оценки и методом сравнения с мерой.
Равноточные измерения. Ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений в одних и тех же условиях.
На практике условие равноточности считается выполненным, если наблюдения производятся одним и тем же оператором, в одинаковых условиях внешней среды, с помощью одного и того же средства измерения. При таких условиях будут получены равнорассеянные (по-другому, равноточные, от слов равная точность), т.е. одинаково распределенные случайные величины.
Неравноточные измерения. Ряд измерений, какой-либо величины, выполненных несколькими различными по точности средствами измерений в нескольких разных условиях.
Однократное измерение - измерение, выполненное один раз. Однократные измерения применяются, когда приоритет принадлежит не точности, а стоимости процесса измерения, или приоритет принадлежит временным нормативам, а также когда наблюдаемое событие быстротечно, или объект измерения меняет свойства и даже разрушается под воздействием процесса измерения.
Многократные измерения. Нахождение размера физической величины с выполнением нескольких следующих друг за другом наблюдений физической величины одного и того же размера. Только многократные измерения позволяют судить о размере случайной погрешности и влиять на размер случайной погрешности, меняя количество наблюдений.
Статические измерения. Измерение физической величины, принимаемой в соответствии с конкретной измерительной задачей за неизменную величину на протяжении времени измерения.
Динамические измерения. Измерение изменяющейся по размеру физической величины.
Технические измерения. Измерения с помощью рабочих средств измерений.
Метрологические измерения. Измерение при помощи эталонов и образцовых средств измерений с целью воспроизведения единиц физических величин для передачи их размера рабочим средствам измерений.
В технических и метрологических измерениях результат находится с требуемой точностью, точность обеспечивается с заданной вероятностью.
Виды и методы измерений. Измерение одной и той же физической величины можно выполнить разными способами. В зависимости от цели измерения, существующие способы можно классифицировать и в каждом случае выбирать лучший из них, как правило - по соотношению между затратами на осуществление измерений и ущербом от недостоверных результатов измерений. Среди многих известных классификаций можно выделить две, построенные по следующим признакам: по способу обработки экспериментальных данных и по способу применения меры. Они получили соответствующие наименования: виды измерений и методы измерений.
В свою очередь, среди видов измерений и методов измерений можно выделить виды и методы, которые применяются наиболее часто. Это прямые измерения и измерения методом непосредственной оценки. Например, измерение силы тока аналоговым амперметром или определение размеров детали при помощи штангенциркуля - прямые измерения методом непосредственной оценки.
При методе непосредственной оценки значение физической величины находят непосредственно по отсчетному устройству измерительного прибора прямого преобразования, шкала которого заранее была отградуирована с помощью меры. При этом не возникает необходимости использовать для измерений дополнительную меру.
При прямых измерениях значение физической величины находят непосредственно по опытным данным в результате выполнения измерения. При этом нет необходимости в дополнительных вычислениях для определения измеряемой физической величины.
2.2. Погрешность, классификация погрешностей
Погрешностью называют отличие между объективно существующим истинным значением физической величины и найденным в результате измерения действительным значением физической величины.
В зависимости от обстоятельств, при которых проводились измерения, а также в зависимости от целей измерения, выбирается та или иная классификация погрешностей. Иногда используют одновременно несколько взаимно пересекающихся классификаций, желая по нескольким признакам точно охарактеризовать влияющие на результат измерения физические величины. В таком случае рассматривают, например, инструментальную составляющую не исключенной систематической погрешности. При выборе классификаций важно учитывать наиболее весомые или динамично меняющиеся или поддающиеся регулировке влияющие величины. Ниже приведены общепринятые классификации согласно типовым признакам и влияющим величинам.
По виду представления, различают абсолютную, относительную и приведенную погрешности.
Абсолютная погрешность это разница между результатом измерения  и истинным значением
и истинным значением  измеряемой величины. Абсолютная погрешность находится как
измеряемой величины. Абсолютная погрешность находится как 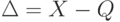 и выражается в единицах измеряемой величины.
и выражается в единицах измеряемой величины.
Относительная погрешность это отношение абсолютной погрешности измерения к истинному значению измеряемой величины: 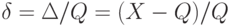 .
.
Приведенная погрешность это относительная погрешность, в которой абсолютная погрешность средства измерения отнесена к условно принятому нормирующему значению  , постоянному во всем диапазоне измерений или его части. Относительная и приведенная погрешности - безразмерные величины.
, постоянному во всем диапазоне измерений или его части. Относительная и приведенная погрешности - безразмерные величины.
В зависимости от источника возникновения, различают субъективную, инструментальную и методическую погрешности.
Субъективная погрешность обусловлена погрешностью отсчета оператором показаний средства измерения.
Инструментальная погрешность обусловлена несовершенством применяемого средства измерения. Иногда эту погрешность называют аппаратурной. Метрологические характеристики средств измерений нормируются согласно ГОСТ 8.009 - 84 [4], при этом различают четыре составляющие инструментальной погрешности: основная, дополнительная, динамическая, интегральная. Согласно этой классификации, инструментальная погрешность зависит от условий и режима работы, а также от параметров сигнала и объекта измерения.
Методическая погрешность обусловлена следующими основными причинами:
- отличие принятой модели объекта измерения от модели, адекватно описывающей его метрологические свойства;
- влияние средства измерения на объект измерения;
- неточность применяемых при вычислениях физических констант и математических соотношений.
В зависимости от измеряемой величины, различают погрешность аддитивную и мультипликативную. Аддитивная погрешность не зависит от измеряемой величины. Мультипликативная погрешность меняется пропорционально измеряемой величине.
В зависимости от режима работы средства измерений, различают статическую и динамическую погрешности.
Динамическая погрешность обусловлена реакцией средства измерения на изменение параметров измеряемого сигнала (динамический режим).
Статическая погрешность средства измерения определяется при параметрах измеряемого сигнала, принимаемых за неизменные на протяжении времени измерения (статический режим).
По характеру проявления во времени, различают случайную и систематическую погрешности.
Систематической погрешностью измерения называют погрешность, которая при повторных измерениях одной и той же величины в одних и тех же условиях остается постоянной или закономерно меняется.
Случайной погрешностью измерения называют погрешность, которая при повторных измерениях одной и той же величины в одних и тех же условиях изменяется случайным образом.
Когда судят о погрешности, подразумевают не значение, а интервал значений, в котором с заданной вероятностью находится истинное значение. Поэтому говорят об оценке погрешности. Если бы погрешность оказалась измеренной, т.е. стали бы известны ее знак и значение, то ее можно было бы исключить из действительного значения измеряемой физической величины и получить истинное значение.
Для получения результатов, минимально отличающихся от истинного значения измеряемой физической величины, проводят многократные наблюдения и проводят математическую обработку полученного массива с целью определения и минимизации случайной составляющей погрешности.
Минимизация систематической погрешности в процессе наблюдений выполняется следующими методами: метод замещения (состоит в замещении измеряемой величины мерой), метод противопоставления (состоит в двух поочередных измерениях при замене местами меры и измеряемого объекта), метод компенсации погрешности по знаку (состоит в двух поочередных измерениях, при которых влияющая величина становится противоположной).
При многократных наблюдениях возможно апостериорное (после выполнения наблюдений) исключение систематической погрешности в результате анализа рядов наблюдений. Рассмотрим графический анализ. При этом результаты последовательных наблюдений представляются функцией времени либо ранжируются в порядке возрастания погрешности [5].
Рассмотрим временную зависимость. Будем проводить наблюдения через одинаковые интервалы времени. Результаты последовательных наблюдений являются случайной функцией времени. В серии экспериментов, состоящих из ряда последовательных наблюдений, получаем одну реализацию этой функции. При повторении серии получаем новую реализацию, отличающуюся от первой.
Реализации отличаются преимущественно из-за влияния факторов, определяющих случайную погрешность, а факторы, определяющие систематическую погрешность, одинаково проявляются для соответствующих моментов времени в каждой реализации. Значение, соответствующее каждому моменту времени, называется сечением случайной функции времени. Для каждого сечения можно найти среднее по всем реализациям значение. Очевидно, что эта составляющая и определяет систематическую погрешность. Если через значения систематической погрешности для всех моментов времени провести плавную кривую, то она будет характеризовать временную закономерность изменения погрешности. Зная закономерность изменения, можем определить поправку для исключения систематической погрешности. После исключения систематической погрешности получаем "исправленный ряд результатов наблюдений".
2.3. Суммирование погрешностей
Оценка расчетным путем результирующей погрешности по известным оценкам ее составляющих называется суммированием погрешностей. В зависимости от требуемой точности, применяются различные методы суммирования погрешностей. Наиболее общим является метод, в котором при суммировании все составляющие погрешности должны рассматриваться как случайные величины.
Согласно ГОСТ 8.207 - 76 [6], случайная погрешность оценивается доверительным интервалом. Однако, при произвольно выбираемых доверительных вероятностях, доверительный интервал суммы не равен сумме доверительных интервалов. В теории вероятностей показано, что суммирование статистически независимых случайных величин осуществляется в виде геометрической суммы их среднеквадратических отклонений (при условии, что суммируемые величины некоррелированы). Если суммируемые составляющие погрешности коррелированы, расчетные соотношения усложняются, суммарное значение погрешности возрастает [7].
Погрешность оценивается с учетом закона распределения результатов наблюдений. Поэтому методика, изложенная в ГОСТ 8.207 - 76 для нормального распределения, не может быть применена для иных видов распределений, иначе может быть получена заниженная или завышенная оценка погрешности. Кроме нормального закона, в технических измерениях часто встречается равномерный закон, например, в распределении систематических погрешностей значений, полученных при многократных наблюдениях, если систематическая погрешность существенно превышает случайную.
Упростить процесс суммирования позволяет пренебрежение малыми погрешностями. Один из возможных вариантов определения критерия ничтожно малой погрешности состоит в том, что если одна величина больше другой на порядок, то ею можно пренебречь.
Основные положения суммирования погрешностей прямых измерений с независимыми многократными наблюдениями устанавливает ГОСТ 8.207 - 76. Эти положения не могут быть распространены на другие виды измерений, т.к. не учитывают те виды погрешностей, которые существенны для них, например, методическую погрешность в совместных измерениях. Соответствующие положения изложены в отдельных нормативных документах. Методика, изложенная в ГОСТ 8.207 - 76, является наиболее общей и может использоваться в качестве составной части других методик измерений.

