Основы общей теории измерений
2.4. Точность и достоверность результата измерения
Применение рассмотренных выше элементов общей теории измерений необходимо для обеспечения точности и достоверности результата измерения. При многократных наблюдениях получают ряд значений, обрабатывая которые находят результат измерения. Для обработки применяют инструменты математической статистики, рассматривая ряд значений как выборку из генеральной совокупности. Опираясь на теорию вероятностей, математическая статистика позволяет оценить надежность и точность выводов, делаемых на основании ограниченного статистического материала.
Точность характеризуется значением, обратным значению относительной погрешности. Величина, обратная абсолютной погрешности, называется мерой точности. В зависимости от требуемой точности, в процессе измерений могут применяться как однократные, так и многократные наблюдения. Если выполняется лишь одно наблюдение, то результат наблюдения является результатом измерения. Если выполняется больше одного наблюдения, результат измерения получают в итоге обработки результатов наблюдений, как правило, в виде среднего арифметического.
Требуемая точность технических измерений может также обеспечиваться повторением многократных наблюдений. В этом случае многократные наблюдения одного и того же объекта выполняются несколько раз. Чтобы сократить время, необходимое для обработки нескольких рядов многократных наблюдений, в начале процесса обработки применяют индикаторы, позволяющие определить предпочтительный ряд и в дальнейшем обрабатывать только этот ряд.
Такими индикаторами является сумма остаточных погрешностей и сумма квадратов остаточных погрешностей. Эти индикаторы являются косвенной характеристикой несмещенности и эффективности оценки, полученной при обработке результатов многократных наблюдений.
Если измерения проводились несколько раз и получено несколько рядов результатов наблюдений, то при одинаковом количестве наблюдений в разных рядах наименьшую сумму остаточных погрешностей будет иметь тот ряд, в котором результаты распределились симметрично относительно среднего арифметического значения, т.е. наиболее близко к нормальному закону. Для дальнейших вычислений рекомендуется выбирать именно его, т.к. он в наибольшей степени будет удовлетворять условию равноточности, а при исключенной систематической погрешности - условию несмещенности оценки результата измерения.
Несмещенная оценка - статистическая оценка, математическое ожидание которой совпадает с оцениваемой величиной. Про несмещенную оценку говорят, что она лишена систематической ошибки.
Однако симметричность не является исчерпывающей характеристикой распределения. Следующим важным в метрологии признаком является компактность распределения. По этому признаку при фиксированном числе наблюдений предпочтительный ряд может быть определен индикатором эффективности. Эффективной называется та из нескольких возможных несмещенных оценок, которая имеет наименьшую дисперсию. Условию эффективности будет удовлетворять ряд с наименьшей суммой квадратов остаточных погрешностей.
Очевидно, что в практической метрологии эффективная оценка является предпочтительной. Признак эффективности свидетельствует о том, что субъективная составляющая случайной погрешности минимальна, наблюдения выполнялись более аккуратно и будет обеспечен наименьший размер случайной погрешности.
В теоретической метрологии рассматривается также состоятельная оценка, являющаяся идеальной моделью для многократных измерений, к которой желательно стремиться, но получить ее практически невозможно. При состоятельной оценке истинное и действительное значение совпадают, погрешность равна нулю. Это достигается бесконечным увеличением числа наблюдений. Состоятельной называется оценка, в которой при числе наблюдений, стремящемся к бесконечности, дисперсия стремится к нулю.
Достоверность результата измерения полагается высокой, если  близка к единице (
близка к единице (  - вероятность, с которой истинное значение физической величины удалено от действительного значения на интервал, не превышающий погрешности). В технических измерениях значение
- вероятность, с которой истинное значение физической величины удалено от действительного значения на интервал, не превышающий погрешности). В технических измерениях значение  , как правило, принимается равным 0,95. Это говорит о том, что если проводить такие измерения 100 раз, то в 95 случаях истинное значение окажется удалено от действительного значения на интервал, размеры которого не превышают погрешности, а в 5 случаях окажется удалено на интервал, превышающий погрешность. Поэтому в измерениях, имеющих непосредственное влияние на безопасность и здоровье, значение
, как правило, принимается равным 0,95. Это говорит о том, что если проводить такие измерения 100 раз, то в 95 случаях истинное значение окажется удалено от действительного значения на интервал, размеры которого не превышают погрешности, а в 5 случаях окажется удалено на интервал, превышающий погрешность. Поэтому в измерениях, имеющих непосредственное влияние на безопасность и здоровье, значение  принимается равным 0,99. Такую же вероятность назначают при однократных измерениях.
Это объясняется тем, что при прочих равных обстоятельствах (в первую очередь, при одинаковом числе наблюдений), размеры
принимается равным 0,99. Такую же вероятность назначают при однократных измерениях.
Это объясняется тем, что при прочих равных обстоятельствах (в первую очередь, при одинаковом числе наблюдений), размеры  и
и  взаимосвязаны: чем больше
взаимосвязаны: чем больше  , тем больше
, тем больше  , следовательно, назначая высокую степень уверенности, мы рассматриваем наихудший вариант контролируемых событий.
, следовательно, назначая высокую степень уверенности, мы рассматриваем наихудший вариант контролируемых событий.
Задавая большую степень неопределенности контролируемым посредством измерений событиям, мы получаем большую уверенность в том, что они произойдут.
Существует способ одновременно увеличивать достоверность и уменьшать неопределенность результата измерений, т.е. увеличивать  и уменьшать
и уменьшать  . Этот способ - увеличение числа наблюдений,
. Этот способ - увеличение числа наблюдений,  . Однако дополнительные наблюдения делают более дорогим процесс измерения. В этой связи актуален рассмотренный в первом разделе вопрос корректной записи результатов измерений.
. Однако дополнительные наблюдения делают более дорогим процесс измерения. В этой связи актуален рассмотренный в первом разделе вопрос корректной записи результатов измерений.
2.5. Прямые равноточные измерения с многократными наблюдениями
ГОСТ 8.207-76 Прямые измерения
Метод прямых равноточных измерений с многократными наблюдениями является основополагающим, используется в технических измерениях для повышения достоверности результата, является основой для многих методов метрологических измерений, для методов косвенных измерений.
Классификация прямых и многократных измерений рассмотрена выше. Требование прямых измерений связано с правилами учета погрешности. Современные средства измерений, как правило, являются сложными устройствами, выполняющими косвенное измерение физических величин. Однако результаты, как правило, рассматриваются как результаты прямых измерений, - поскольку погрешность косвенных измерений внутри средства измерений уже учитывается его классом точности.
Равноточность измерений истолковывается в широком смысле, как одинаковая распределенность (в узком смысле равноточность измерений понимается как одинаковость меры точности всех результатов измерений). Наличие грубых ошибок (промахов) означает нарушение равноточности как в широком, так и в узком смысле.
На практике условие равноточности считается выполненным, если наблюдения производятся одним и тем же оператором, в одинаковых условиях внешней среды, с помощью одного и того же средства измерения. При таких условиях будут получены равнорассеянные (по-другому, равноточные, от слов равная точность), т.е. одинаково распределенные случайные величины
Метод прямых равноточных измерений с многократными наблюдениями изложен в ГОСТ 8.207 - 76. В этом разделе дополнительно к ГОСТ 8.207 - 76 приводятся необходимые для выполнения расчетов сведения и комментарии.
Комментарии к ГОСТ 8.207 - 76. Раздел 2. Результат измерения и оценка его среднего квадратического отклонения
Результат измерения находят как среднее арифметическое результатов наблюдений:
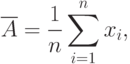
где  - число наблюдений.
- число наблюдений.
Для оценки среднего квадратического отклонения результата измерения находим случайные отклонения результатов отдельных наблюдений, принимаем их за остаточные погрешности,
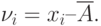
Для минимизации случайной и систематической составляющих погрешности, при наличии нескольких групп наблюдений (реализаций), используют два свойства остаточных погрешностей: сумма остаточных погрешностей равна нулю,

и сумма квадратов остаточных погрешностей минимальна,

Для дальнейших вычислений рекомендуется выбрать реализацию, удовлетворяющую этим условиям.
Степень рассеяния результатов наблюдений вокруг среднего арифметического значения характеризуется средним квадратическим отклонением, (СКО):
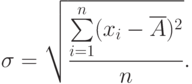
Среднее квадратическое отклонение результатов наблюдения - числовая характеристика из теории вероятности, в практической метрологии вместо него применяется оценка СКО:
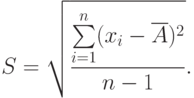
Оценка СКО учитывает ограниченность объем а выборки: при малом объем е выборки оценка СКО будет заметно больше, чем СКО, а при большом объем е выборки оценка СКО не будет заметно отличаться от СКО.
Полученное значение СКО результатов наблюдения не так универсально, как среднее арифметическое исправленных результатов наблюдений и не может быть непосредственно принято за значение случайной погрешности результата измерения. Для этого, прежде всего, необходимо восстановить размерность физической величины, ликвидировав нелинейность преобразования физической величины, разделив СКО результатов наблюдения на корень из  . Полученное значение принимают за оценку среднего квадратического отклонения результата измерения:
. Полученное значение принимают за оценку среднего квадратического отклонения результата измерения:
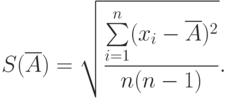
Комментарии к ГОСТ 8.207 - 76. Раздел 4. Доверительные границы не исключенной систематической погрешности результата измерения
Источники систематической погрешности разнообразны. Ее могут вызвать условия измерения, метод измерения, особенности средства измерения и другие причины. Существенный вклад вносит и трудно исключается инструментальная составляющая систематической погрешности. Эту составляющую будем рассматривать в качестве не исключенной систематической погрешности. При этом различаются основная и дополнительная инструментальная погрешность. Обе погрешности определяются классом точности средства измерения. Дополнительная погрешность возникает при выходе условий измерения за нормальные пределы и принимается равной удвоенному значению основной погрешности.
Предположим, что наблюдения были получены в результате измерения цифровым вольтметром, имеющим класс точности, обозначенный цифрой 1,5 в кружочке, причем условия измерения выходили за нормальные пределы.
Основная инструментальная погрешность:
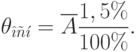
Дополнительная инструментальная погрешность:
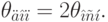
Вычисление систематической составляющей погрешности,  и случайной составляющей погрешности,
и случайной составляющей погрешности,  , а также определение на их основе погрешности результата измерения,
, а также определение на их основе погрешности результата измерения,  , выполняется согласно ГОСТ 8.207 - 76.
, выполняется согласно ГОСТ 8.207 - 76.

